算法扩展
(以下算法出自 算法爱好者 ,由本人精简,拓展学习。版权所有http://www.cnblogs.com/ytlds/)
1、最小栈的实现
实现一个栈,带有出栈(POP),入栈(PUSH),取最小元素(getMin)三个方法,保证方法时间复杂度为O(1)
步骤:①创建2个栈A、B,B用来辅助A
②第一个元素进栈时,元素下标进入栈B,此时这个元素就是最小元素
③当有新元素入栈时,比较该元素与栈A中的最小值,若比其小,将其下标存入栈B
④不管入栈出栈,只需取栈B顶的下标
2、判断2的乘方
实现一个方法,判断正整数是否是2的乘方,要求性能尽可能高(提示:2的乘方数2、4、8、16......,其二进制中只有一位1,(10B、100B、1000B,再将2的乘方数减去1转成二进制,全是(1B、11B、111B...)))
步骤:①将2的乘方数与其减1做与运算
②结果为0,则为2的乘方
public static boolean method(int num){ return (num&(num-1))==0; }
3、找出缺失的整数
一个无序数组里有若干个正整数,范围从1到100,其中99个整数都出现了偶数次,只有一个整数出现了奇数次(比如1,1,2,2,3,3,4,5,5),如何找到这个出现奇数次的整数
步骤:遍历整个数组,依次做异或运算。由于异或在位运算时相同为0,不同为1,因此所有出现偶数次的整数都会相互抵消变成0,只有唯一出现奇数次的整数会被留下。
扩展:一个无序数组里有若干个正整数,范围从1到100,其中98个整数都出现了偶数次,只有两个整数出现了奇数次(比如1,1,2,2,3,4,5,5),如何找到这个出现奇数次的整数
步骤:遍历整个数组,依次做异或运算。由于数组存在两个出现奇数次的整数,所以最终异或的结果,等同于这两个整数的异或结果。这个结果中,至少会有一个二进制位是1(如果都是0,说明两个数相等,和题目不符)。
eg:如果最终异或的结果是5,转换成二进制是00000101。此时我们可以选择任意一个是1的二进制位来分析,比如末位。把两个奇数次出现的整数命名为A和B,如果末位是1,说明A和B转为二进制的末位不同,必定其中一个整数的末位是1,另一个整数的末位是0。根据这个结论,我们可以把原数组按照二进制的末位不同,分成两部分,一部分的末位是1,一部分的末位是0。由于A和B的末位不同,所以A在其中一部分,B在其中一部分,绝不会出现A和B在同一部分,另一部分没有的情况。这样我们的问题又回归到了上一题的情况,按照原先的异或解法,从每一部分中找出唯一的奇数次整数即可。
4、求两个整数的最大公约数
拓展:
辗转相除法(前提:两个正整数a和b(a>b),它们的最大公约数等于a除以b的余数c和b之间的最大公约数。比如10和25,25除以10商2余5,那么10和25的最大公约数,等同于10和5的最大公约数)
public static int getNum(int A, int B){ int result = 1; if(A > B) result = gcd(A,B); else result = gcd(B,A); return result; } private static int gcd(int a, int b){ if(a%b == 0) return b; else return gcd(b, a%b); }
问题:整数过大,a%b取模性能会比较低
更相减损术(前提:两个正整数a和b(a>b),它们的最大公约数等于a-b的差值c和较小数b的最大公约数。比如10和25,25减去10的差是15,那么10和25的最大公约数,等同于10和15的最大公约数)
public static int gcd(int A, int B){ if(A == B) return A; if(A < B) return gcd(B - A, A); else return gcd(A - B, B); }
问题:两个整数过大求差运算次数较多
步骤:结合两种算法,通过移位运算
public static int gcd(int A, int B){ if (A == B) return A; if (A > B) return gcd(B , A); else if ((!A&1) && (!B&1)) return gcd(A>>1, B>>1) << 1; else if ((!A&1) && (B&1)) return gcd(A>>1, B); else if ((A&1) && (!B&1)) return gcd(A, B>>1); else return gcd(A, A-B); }
5、动态规划(核心:最优子结构、边界、状态转移方程式)
有一座高度是10级台阶的楼梯,从下往上走,每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法
提示:0~9级走法有X种,0~8级走法有Y种,那么F(10) = F(9) + F(8),最后依次递归
public int getCon(int n){ if (n < 1) return 0; if (n == 1) return 1; if (n == 2) return 2; return getCon(n-1) + getCon(n-2); }
简单递归的时间复杂度较高,可以使用备用录算法
public int getCon(int n, HashMap<Integer, Integer> map){ if (n < 1) return 0; if (n == 1) return 1; if (n == 2) return 2; if (map.contains(n)){ return map.get(n); }else { int value = getCon(n-1,map) + getCon(n-2,map); map.put(n, value); return value; } }
备用录算法中哈希表中存入多个结果,继续优化(逆转方向)
public int getCon(int n){ if (n < 1) return 0; if (n == 1) return 1; if (n == 2) return 2; int a=1, b=2, temp=0; // 每一个结果都只需要用到前面的两个结果 for (int i=3; i<n; i++){ temp = a + b; a = b; b = temp; } return temp; }
有一个国家发现了5座金矿,每座金矿的黄金储量不同,需要参与挖掘的工人数也不同。参与挖矿工人的总数是10人。每座金矿要么全挖,要么不挖,不能派出一半人挖取一半金矿。要求用程序求解出,要想得到尽可能多的黄金,应该选择挖取哪几座金矿
提示:分析最优子结构(第五个金矿可以不挖可以挖,所以有两个最优子结构。不挖时即4个金矿10个工人,挖时即4个金矿[10-第5金矿工人]),那么5个金矿最优选择也有两个了
把金矿数量设为N,工人设为M,金矿黄金量设为数组G[],金矿用工量设为P[],那么存在的最优关系就是F(5,10) = MAX( F(4,10) , F(4,10-P[4])+G[4] )。
边界:若工人数量不够挖一座金矿,则
N=1,W>=P[0],F(N,W) = G[0];
N=1,W<P[0],F(N,W) = 0;
得到状态转移方程式
F(n,w) = 0 (n<=1, w<p[0]);
F(n,w) = g[0] (n==1, w>=p[0]);
F(n,w) = F(n-1,w) (n>1, w<p[n-1])
F(n,w) = max(F(n-1,w), F(n-1,w-p[n-1])+g[n-1]) (n>1, w>=p[n-1])
实现方法有简单递归、备忘录算法、动态规划(自底向上递推)
int getMostGold(int n, int w, int[] g, int[] p){ int[] preResult = new int[p.length]; int[] results = new int[p.length]; for (int i=0; i<=n; i++){ if (i < p[0]) preResult[i] = 0; else preResult[i] = g[0]; } for (int i=0; i<n; i++){ for (int j=0; j<=w; j++){ if (j<p[i]){ results[j] = preResult[j]; }else { results[j] = Math.max(preResult[j], preResult[j-p[i]] + g[i]); } } preResult = results; } return results[n]; }
6、跳跃表——基于有序链表的扩展
更快查找到一个有序链表的某节点
步骤:
取出链表的一层关键节点作为索引,然后再取出二层的关键节点作为索引,最后只剩连个关键节点即可。所以要插入的新节点就需要逐步的去和索引比较确定范围,最后插入即可
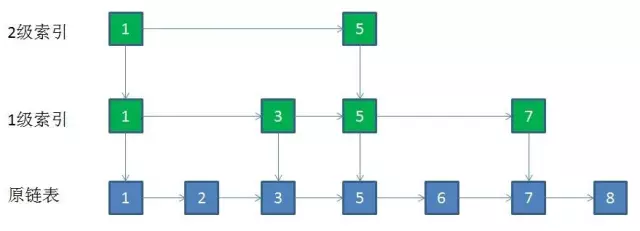
问题:插入新节点之后,索引会变的不够用。最终采取随机方式"提拔"上索引。
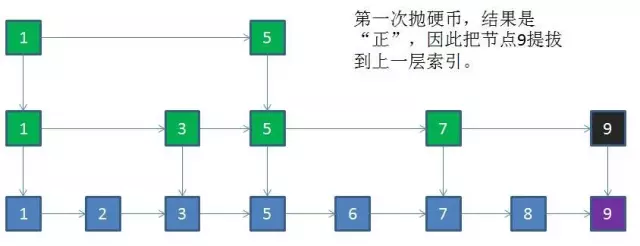
插入的步骤:
-
新节点和各层索引节点逐一比较,确定原链表的插入位置。O(logN)
-
把索引插入到原链表。O(1)
-
利用抛硬币的随机方式,决定新节点是否提升为上一级索引。结果为“正”则提升并继续抛硬币,结果为“负”则停止。O(logN)
删除的步骤:
在索引层找到要删除的节点,那么删除每一层的相同节点
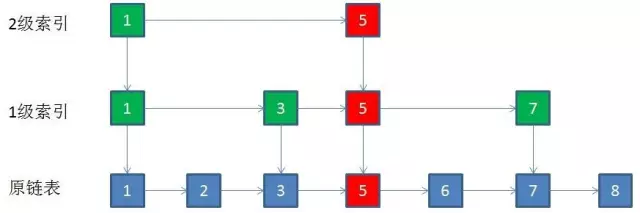
-
自上而下,查找第一次出现节点的索引,并逐层找到每一层对应的节点。O(logN)
-
删除每一层查找到的节点,如果该层只剩下1个节点,删除整个一层(原链表除外)。O(logN)
7、B-树——MySQL数据库索引主要基于B+树和Hash表
首先数据库索引都是存储在磁盘上,当数据量大响应的索引大小也增加
一个m阶的B树有如下几个特征:
1.根结点至少有两个子女。
2.每个中间节点都包含k-1个元素和k个孩子,其中 m/2 <= k <= m
3.每一个叶子节点都包含k-1个元素,其中 m/2 <= k <= m
4.所有的叶子结点都位于同一层。
5.每个节点中的元素从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域分划。

这颗树中,看(2,6)节点。该节点满足所有特征:
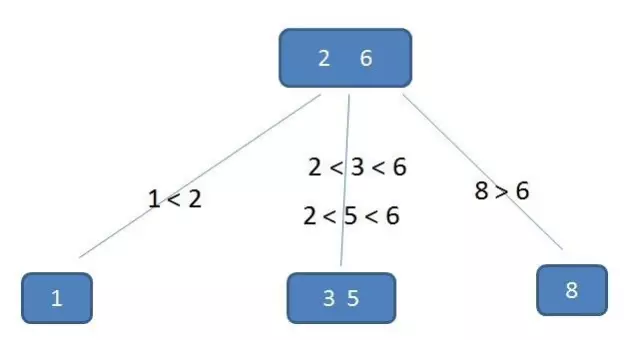
具体的B-树的插入和删除本人尚不能用言语表达~~遗憾!!!~~
应用:B-树主要应用于文件系统以及部分数据库索引,比如非关系型数据库MongoDB。而大部分关系型数据库,比如MySQL,则使用B+树作为索引
8、B+树
基于B-树的一种变体,有着比B-树更高的查询性能。
一个m阶的B+树具有如下几个特征:
1.有k个子树的中间节点包含有k个元素(B树中是k-1个元素),每个元素不保存数据,只用来索引,所有数据都保存在叶子节点。
2.所有的叶子结点中包含了全部元素的信息,及指向含这些元素记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
3.所有的中间节点元素都同时存在于子节点,在子节点元素中是最大(或最小)元素。
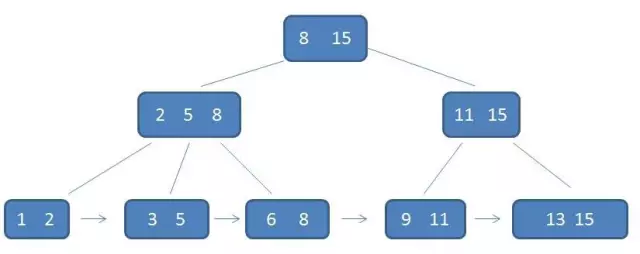
B+树相比B-树的优势有三个:①、单一节点存储更多元素,使查询IO次数更少。②、所有查询都要查找到叶子节点,查询性能稳定。3、所有叶子节点形成有序链表,范围查询简便。
B+树的插入和删除类似B-树。
9、Base64算法
Base64算法只支持64个【可打印字符】。Base64可把原来ASCII码的控制字符甚至ASCII码之外的字符转换成可打印的6bit字符(原来的字节码是8bit),如下图:8bit字符串[Man]编码成Base64的[TWFu]
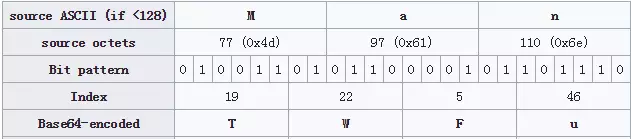
如果有多余的bit位,补0即可,没有匹配的8bit字符,则使用[=]字符填充,如下图:8bit字符串[M]编码成Base64的[TQ==]

10、 MD5算法
算法过程分为四步:处理原文、设置初始值、循环加工、拼接结果
具体算法过程请自行参考代码......
11、SHA算法
分类:SHA-1算法(已淘汰,可破解)、SHA-2、SHA-3(已问世)
SHA-2算法又分为多个版本:(信息摘要越长,破解难度越大。但同时耗费性能和占用空间也越高)
SHA-256:可以生成长度256bit的信息摘要。
SHA-224:SHA-256的“阉割版”,可以生成长度224bit的信息摘要。
SHA-512:可以生成长度512bit的信息摘要。
SHA-384:SHA-512的“阉割版”,可以生成长度384bit的信息摘要。
12、AES算法
在Java的java.crypto包有很好包装,具体的密钥、填充方式、工作模式暂且不讨论。
public static void main(String[] args) { String content = "test"; String password = "123456"; // 加密 byte[] encry = encrypt(content,password); System.out.println(encry); // 解密 System.out.println(new String(decrypt(encry,password))); } public static byte[] encrypt(String content, String password) { KeyGenerator kgen = null; try { kgen = KeyGenerator.getInstance("AES"); kgen.init(128, new SecureRandom(password.getBytes())); SecretKey secretKey = kgen.generateKey(); byte[] enCodeFormat = secretKey.getEncoded(); SecretKeySpec key = new SecretKeySpec(enCodeFormat, "AES"); Cipher cipher = Cipher.getInstance("AES");// 创建密码器 cipher.init(Cipher.ENCRYPT_MODE, key);// 初始化 byte[] byteContent = content.getBytes("utf-8"); byte[] result = cipher.doFinal(byteContent); return result;//加密 } catch (NoSuchAlgorithmException | InvalidKeyException | NoSuchPaddingException | BadPaddingException | UnsupportedEncodingException | IllegalBlockSizeException e) { e.printStackTrace(); } return null; } /** * 解密 * * @param content 待解密内容 * @param password 解密密钥 * @return */ public static byte[] decrypt(byte[] content, String password) { KeyGenerator kgen = null; try { kgen = KeyGenerator.getInstance("AES"); kgen.init(128, new SecureRandom(password.getBytes())); SecretKey secretKey = kgen.generateKey(); byte[] enCodeFormat = secretKey.getEncoded(); SecretKeySpec key = new SecretKeySpec(enCodeFormat, "AES"); Cipher cipher = Cipher.getInstance("AES");// 创建密码器 cipher.init(Cipher.DECRYPT_MODE, key);// 初始化 byte[] result = cipher.doFinal(content); return result; // 解密 } catch (NoSuchAlgorithmException | BadPaddingException | IllegalBlockSizeException | NoSuchPaddingException | InvalidKeyException e) { e.printStackTrace(); } return null; }
13、红黑树——是一种自平衡的二叉树
二叉树的特征:
1.左子树上所有结点的值均小于或等于它的根结点的值。
2.右子树上所有结点的值均大于或等于它的根结点的值。
3.左、右子树也分别为二叉排序树

红黑树除了符合二叉树的基本特征外,还符合下列特性:
1.节点是红色或黑色。
2.根节点是黑色。
3.每个叶子节点都是黑色的空节点(NIL节点)。
4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
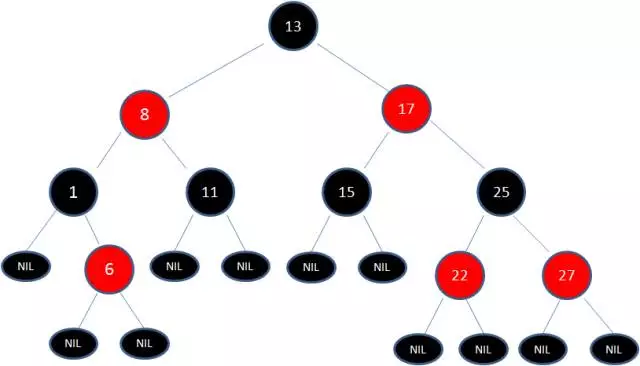
红黑树从根到叶子的最长路径不会超过最短路径的2倍。当插入或删除节点时破坏规则,需要调整。其中经过具体的旋转(左右旋转)、变色使红黑树重新符合规则。
应用:JDK的集合类TreeMap和TreeSet底层就是红黑树实现。在Java8中,连HashMap也用到红黑树。
14、HashMap
HashMap是一个用于存储Key-Value键值对的集合,每个键值对也叫Entry。这些Entry分散存储在一个数组中,这个数组就是HashMap的主干。
HashMap数组每个元素初始值都是NULL,我们最常用的方法是Get和Put
Put的原理:
HashMap数组的每个元素不止是一个Entry对象,也是一个链表的头节点。每个Entry对象通过Next指针指向它的下个Entry节点。当新插入的Entry映射到冲突的数组位置时,只需插入对应链表(头插法,不插入尾部)。
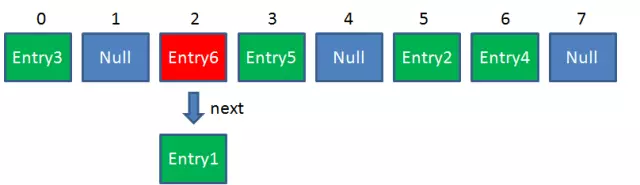
Get的原理:
首先使用输入的key做一次Hash映射,得到对应index。此时就会找到对应的Entry链表,再在链表中依次找到key值。
问题:HashMap默认的初始长度是多少?
答:初始长度为16,每次自动扩展或是手动初始化时,长度必须是2的幂
选择16的原因是服务于从key映射到index的Hash算法(因为从Key映射到HashMap数组的位置,会用到一个Hash函数:index = Hash("apple"))。为了实现一个尽量均匀分布的Hash函数,我们通过利用Key的HashCode值来做位运算。
获得如下Hash函数(Length是HashMap长度):index = HashCode(Key) & (Length - 1);
15、高并发的HashMap
问题:高并发情况下,为什么HashMap可能出现死锁?Java8中,HashMap的结构有怎样的优化?
ReHash:是HashMap在扩容时候的一个步骤。当经过多个元素插入,Key映射位置发生冲突几率会逐渐提高。此时HashMap扩展长度,进行Resize。
Resize的条件是:HashMap.Size >= Capacity * LoadFactor
1.Capacity:HashMap的当前长度。上一期曾经说过,HashMap的长度是2的幂。
2.LoadFactor:HashMap负载因子,默认值为0.75f。
Resize步骤:
1.扩容:创建一个新的Entry空数组,长度是原数组的2倍。
2.ReHash:遍历原Entry数组,把所有的Entry重新Hash到新数组。为什么要重新Hash呢?因为长度扩大以后,Hash的规则也随之改变。
答:以上操作在单线程执行并无问题,在多线程环境,会形成死循环。(具体形成原因请查看原漫画!!!)
通常高并发情况下,通常采用另一个集合类ConcurrentHashMap。这个集合类兼顾了线程安全和性能。
16、ConcurrentHashMap
ConcurrentHashMap的结构:
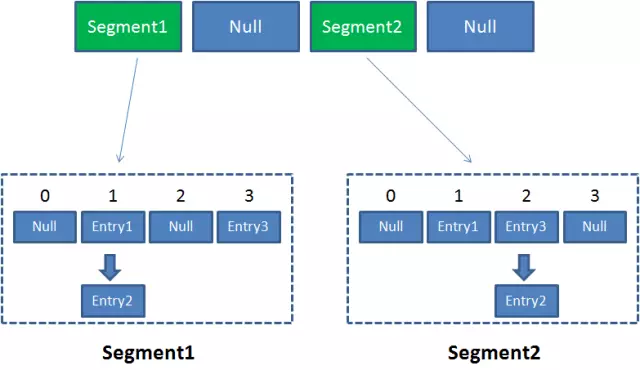
Segment本身相当于一个HashMap对象,ConcurrentHashMap集合中有2的N次方个,共同保存在一个名为segment的数组中。可以说,ConcurrentHashMap是一个二级哈希表。在一个总的哈希表下面,有若干个子哈希表。
优势:采用了【锁分段技术】,每个Segment就好比一个自治区,读写操作高度自治,互不影响。
以下是几种并发读写的情形:
case1:不同Segment的并发写入(不同Segment的写入是可并发执行的)
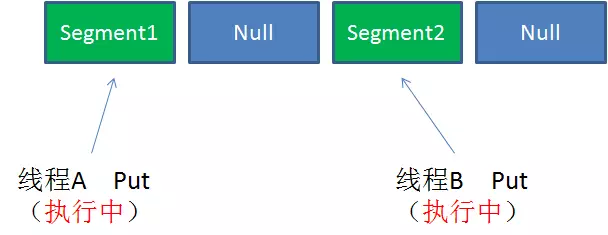
case2:同一Segment的一写一读(是可以并发执行的)
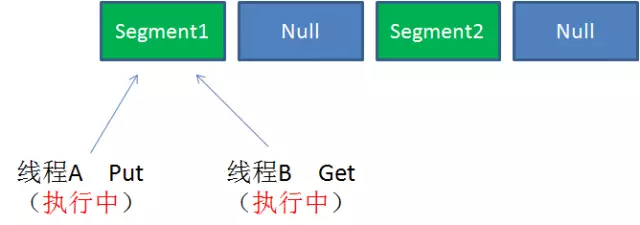
case3:同一Segment的并发写入(Segment写入需要上锁,对同一Segment的并发写入会被阻塞)
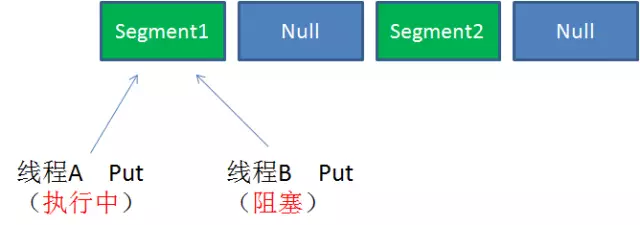
ConcurrentHashMap当中每个Segment各自有锁。在保证线程安全的同时降低了锁的粒度,让并发操作效率更高。
Get方法:
1.为输入的Key做Hash运算,得到hash值。
2.通过hash值,定位到对应的Segment对象
3.再次通过hash值,定位到Segment当中数组的具体位置。
Put方法:
1.为输入的Key做Hash运算,得到hash值。
2.通过hash值,定位到对应的Segment对象
3.获取可重入锁
4.再次通过hash值,定位到Segment当中数组的具体位置。
5.插入或覆盖HashEntry对象。
6.释放锁。
在统计ConcurrentHashMap的Size()时,怎么保证一致性?
1.遍历所有的Segment。
2.把Segment的元素数量累加起来。
3.把Segment的修改次数累加起来。
4.判断所有Segment的总修改次数是否大于上一次的总修改次数。如果大于,说明统计过程中有修改,重新统计,尝试次数+1;如果不是。说明没有修改,统计结束。
5.如果尝试次数超过阈值,则对每一个Segment加锁,再重新统计。
6.再次判断所有Segment的总修改次数是否大于上一次的总修改次数。由于已经加锁,次数一定和上次相等。
7.释放锁,统计结束。
17、单例模式
(由于本人以前接触过单例模式,博客中也有描述,就不过多介绍)
下面代码是懒汉式代码,基本是线程安全(【反射】的方式仍可以构建多个实例对象):
public class Singleton { private Singleton() {} //私有构造函数 private volatile static Singleton instance = null; //单例对象 //静态工厂方法 public static Singleton getInstance() { if (instance == null) { //双重检测机制 synchronized (this){ //同步锁 if (instance == null) { //双重检测机制 instance = new Singleton(); } } } return instance; } }
其中关于volatile关键字阻止了变量访问前后的指令重排,保证指令执行顺序。也可以保证线程访问的变量值是主内存中的最新值。
利用反射打破单例模式约束:
//获得构造器 Constructor con = Singleton.class.getDeclaredConstructor(); //设置为可访问 con.setAccessible(true); //构造两个不同的对象 Singleton singleton1 = (Singleton)con.newInstance(); Singleton singleton2 = (Singleton)con.newInstance(); //验证是否是不同对象 System.out.println(singleton1.equals(singleton2));
防止反射构建对象,只需要用枚举实现单例模式即可,因为JVM会阻止反射获取枚举类的私有构造方法。
enum Singleton{ INSTANCE; } public class SingletonTest { public static void main(String[] args) { Singleton s=Singleton.INSTANCE; Singleton s2=Singleton.INSTANCE; System.out.println(s==s2); } }
enum Singleton2{ INSTANCE{ @Override protected void read() { System.out.println("read"); } @Override protected void write() { System.out.println("write"); } }; protected abstract void read(); protected abstract void write(); } public class SingletonTest2 { public static void main(String[] args) { Singleton2 s=Singleton2.INSTANCE; s.read(); } }
以上是两种枚举实现单例模式的方式(仅做参考)。但是对于原来的单例方式,想要序列化,但是又想反序列化,则必须实现readResolve方法
class SingletonB implements Serializable { private static SingletonB instence = new SingletonB(); private SingletonB() { } public static SingletonB getInstance() { return instence; } // 不添加该方法则会出现 反序列化时出现多个实例的问题 public Object readResolve() { return instence; } }
18、排序算法
①、桶排序(浪费空间,小数不好排序)
考试分数:5分、2分、7分、5分、3分、8分(总分10分),排序?
答:新建一个长度为11的数组(长度就是0~10分),考试的分数如果为5分,则在a[5]上加1,当所有考试分数都循环完后,数组的值为0、0、1、1、0、2、0、1、1、0、0,可以看出数组的值即为分数出现的个数,然后for循环输出 a[i]次 数组的下标就是排序后的分数。
②、冒泡排序
将【12、35、99、18、76】从大到小排序
答:比较【12】和【35】大小,大的往前,所以交换它们,新结构为【35、12、99、18、76】,继续比较第二、三位【12】和【99】,最终当比较4次之后,最小【12】到最后一位。重新开始从第一、二位比较【35】和【99】,最后循环结束。一般需要循环a[n].length - 1次即可成功。
③、快速排序
对“6 1 2 7 9 3 4 5 10 8”排序
答:以“6”为基准,设置两个变量 i 、 j ,分别指向首尾元素。让 j 先往左移, i 往右移,当 j 指向比基准小的数时stop,当 i 指向比基准大的数时stop,然后交换这两个值,但是 i 、 j 不动,继续按原方向移动,满足条件就交换。当 i 、 j 指向同一个数时stop,此时交换基准“6”和这个数,第一次排序就好了(左边比“6”小,右边比“6”大)。同样的,将“6”的左右两边按刚刚的方法再排序,一直递归下去,就会得到从小到大排序的一组数字了。
public static int Partition(int[] a,int p,int r){ int x=a[r-1]; int i=p-1; int temp; for(int j=p;j<=r-1;j++){ if(a[j-1]<=x){ // 交换(a[j-1],a[i-1]); i++; temp=a[j-1]; a[j-1]=a[i-1]; a[i-1]=temp; } } //交换(a[r-1,a[i+1-1]); temp=a[r-1]; a[r-1]=a[i+1-1]; a[i+1-1]=temp; return i+1; } public static void QuickSort(int[] a,int p,int r){ if(p<r){ int q=Partition(a,p,r); QuickSort(a,p,q-1); QuickSort(a,q+1,r); } } //main方法中将数组传入排序方法中处理,之后打印新的数组 public static void main(String[] stra){ int[] a={7,10,3,5,4,6,2,8,1,9}; QuickSort(a,1,10); for (int i=0;i<a.length;i++) System.out.println(a[i]); }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号