爱恨交织的红黑树
虐你千万遍,还要待她如初恋的红黑树,是否对她既欢喜又畏惧。别担心,通过本文讲解,希望你能有前所未有的感动。
红黑树也是二叉查找树,但比普通的二叉查找树多一些特性条件限制,每个结点上都存储有红色或黑色的标记。因为是二叉查找树,所以他拥有二叉查找树的所有特性。红黑树是一种自平衡二叉查找树,在极端数据条件插入时(正序或倒叙)不会退化成类链状数据,可以更高效的在O(log(n))时间内完成查找,插入,删除操作。
准备
在阅读本文之前,建议先阅读我上篇文章《二叉查找树的解读和实现》,可以更好的帮助你理解红黑树。
特性
- 结点是红色或黑色
- 根结点必须为黑色
- 叶子结点(约定为null)一定为黑色
- 任一结点到叶子结点的每条路径上黑色结点数量都相等
- 不允许连续两个结点都为红色,也就是说父结点和子结点不能都为红色
查找
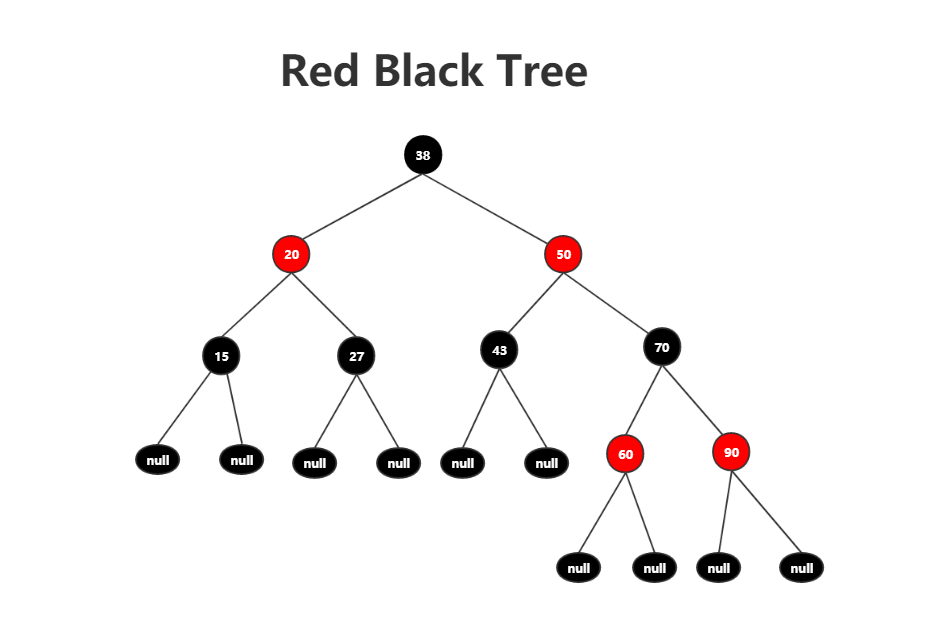
红黑树的查找方式和上篇文章所讲述的原理一样,这里就不重新讲述,以结点[38,20,50,15,27,43,70,60,90]为例,返回一颗红黑树。
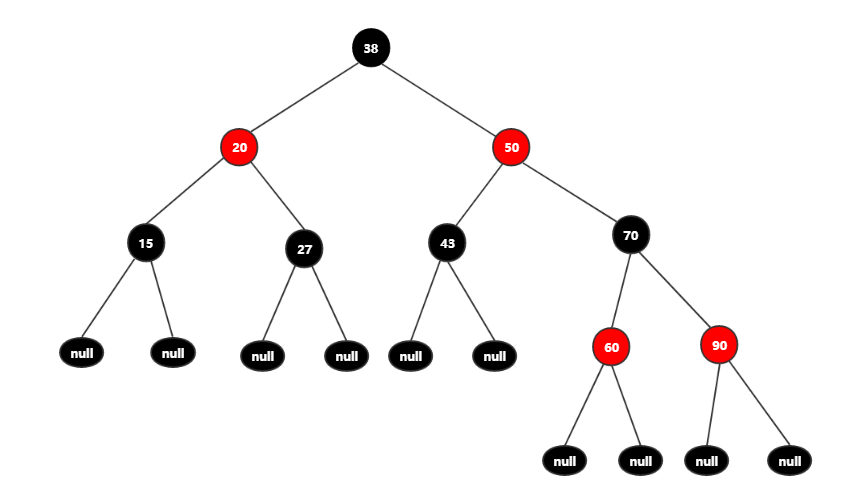
普通操作
红黑树的插入和删除,分为多种情况,相对来说比较复杂。插入或删除新结点后的树,必须要满足上面五点特性的二叉查找树,所以要通过不同手段来调整树。但普通操作就是和普通二叉查找树操作一样。
比如普通插入中,因为每个结点只能是红色或黑色,所以我们定义新添加的非根结点默认颜色为红色。将新结点定义为红色的原因是为了满足特性4(任一结点到叶子结点的每条路径上黑色结点数量都相等),否则会多出一个黑色结点打破规则。
现在向树中插入结点10。
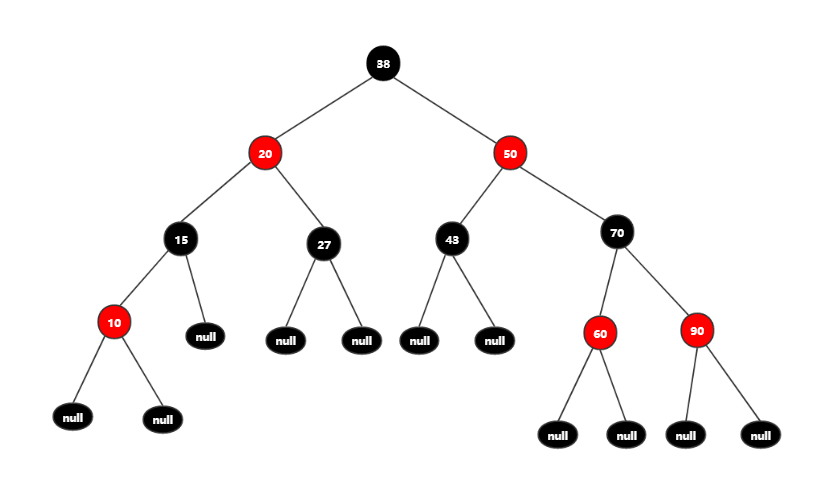
从图中可以看到,父结点15为黑色结点,插入红色结点10,不会增加黑色结点的数量,其他规则也没有受到影响,所以,当插入结点的父结点为黑色时,直接插入树中,不会破坏原红黑树的规则。
该种情况代码实现:
结点对象
package com.ytao.rbt;
/**
* Created by YANGTAO on 2019/11/9 0009.
*/
public class Node {
public static String RED = "red";
public static String BLACK = "black";
public Integer value;
public String color;
public Node left;
public Node right;
public Node(Integer value, String color, Node left, Node right) {
this.value = value;
this.color = color;
this.left = left;
this.right = right;
}
public Node(int value, String color) {
this.value = value;
this.color = color;
}
}
实现操作
public void commonInsert(Node node, Integer newVal){
if (node == null)
node = new Node(newVal, Node.BLACK);
while (true){
if (newVal < node.value){
if (node.left == null){
// 如果左树为叶子结点并且父结点为黑色,可以直接插入红色新结点
if (node.color == Node.BLACK){
node.left = new Node(newVal, Node.RED);
break;
}
}
node = node.left;
}else if (newVal > node.value){
if (node.right == null){
if (node.color == Node.BLACK){
node.right = new Node(newVal, Node.RED);
break;
}
}
node = node.right;
}
}
}
看到这段代码,是否似曾相识的感觉,没错,这就是上篇文章的插入操作加了个颜色限制。
同样删除也是如此,这里就不在细述。
变色
为了更好分析清楚变色的原因,我们将树中的50结点提取出来作为根结点,如图:
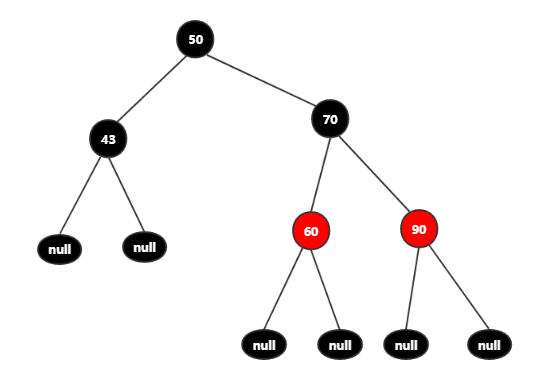
向树中添加结点55,得到树如图:
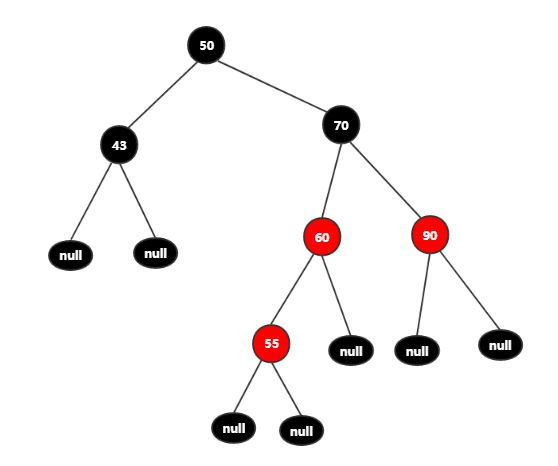
这时55和60都为红色结点,不符合红黑树的特性(不允许连续两个结点都为红色),这时我们需要调整,就使用到变色。
将父结点60变为黑色,又遇到不符合红黑树特性(任一结点到叶子结点的每条路径上黑色结点数量都相等),因为我们增加了黑色结点60,多出了一个黑色结点。
这时的结点70一定为黑色,因为原本的父结点60的颜色为红色。将结点70变为红色,满足了结点70的左子树,但右子树受结点70变为红色的影响,少了个黑色结点,刚好结点90为红色,可以将其变为黑色,满足结点70的右子树要求。
该种特殊情况较为简单处理,只需通过变色就能处理。
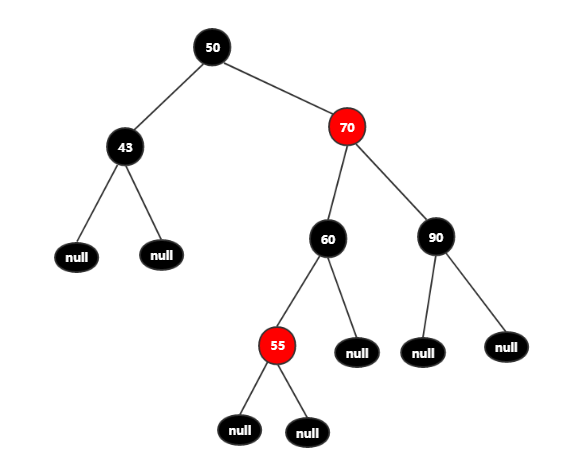
这种条件结构的红黑树实现:
public void changeColor(Node node, int newVal){
if (node.left == null || node.right == null)
return;
// 通过判断待插入结点的父结点和叔叔结点,是否满足我们需要的条件
if (node.left.color == Node.RED && node.right.color == Node.RED){
// 确定是更新到左树还是右树中
Node base = compare(newVal, node.value) > 0 ? node.right : node.left;
// 和待插入结点的父结点作比较
if (newVal < base.value && base.left == null){
base.left = new Node(newVal, Node.RED);
}else if (newVal > base.value && base.right == null){
base.right = new Node(newVal, Node.RED);
}
}
node.color = Node.RED;
// 通过取反获取插入结点的叔叔结点并将颜色变黑色
Node uncleNode = compare(newVal, node.value) > 0 ? node.left : node.right;
uncleNode.color = Node.BLACK;
}
public int compare(int o1, int o2){
if (o1 == o2)
return 0;
return o1 > o2 ? 1 : -1;
}
旋转
当仅仅通过变色无法解决我们需要满足特性时,我们就要考虑使用红黑树的旋转。
旋转在插入和删除中,会频繁用到该操作,为了满足我们的五条特性,通过旋转可以生成一颗新的红黑树,旋转分为左旋转和右旋转。
左旋转
左旋转为逆时针的旋转,类似于把父结点往左边拉(可以这么记忆区分左右旋转的方向),变换如图:
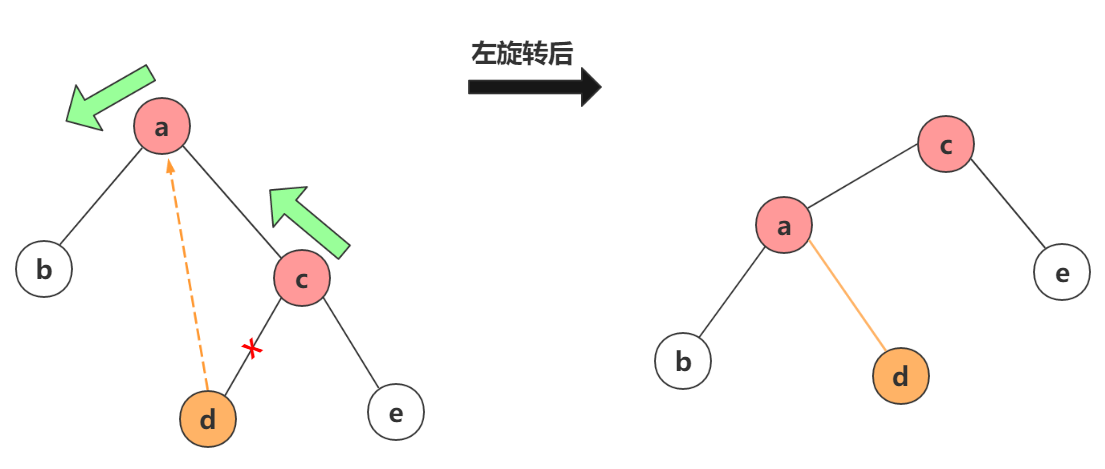
右旋转
右旋转与左旋转出方向相反外,其他都一样,变换如图:
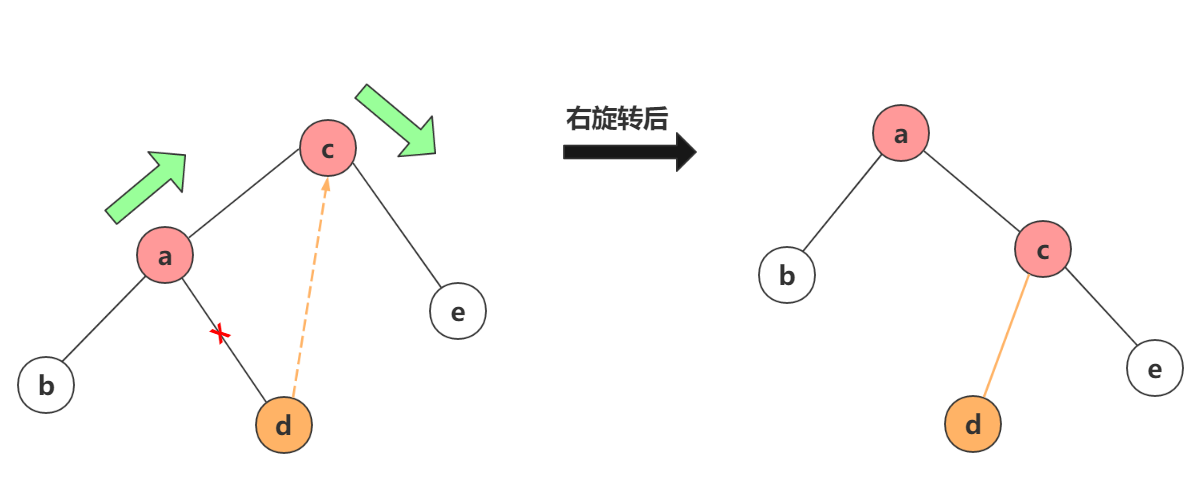
从图中可以看出,旋转后的父子结点,关系对调了,同时子结点的子结点给了父结点。
如果是左旋转,那么父结点会成为旋转结点的左子结点;子结点的左子结点会成为父结点的右子结点。
如果是右旋转,那么父结点会成为旋转结点的右子结点;子结点的右子结点会成为父结点的左子结点。
听起来比较比较拗口,记住一条规则,左小右大,结合上图两个旋转就比较好理解。
用代码实现旋转如下:
/**
*
* @param node 两个旋转结点中的父结点
* @param value 两个旋转结点中子结点的值,因为在整合旋转的时候,node可以遍历查找出来,value作为需要旋转的标记结点
*/
public void rotate(Node node, int value){
Node nodeChild = compare(value, node.value) > 0 ? node.right : node.left;
if (nodeChild != null && value == nodeChild.value){
Node parent = node;
// 旋转子结点小于旋转父结点,执行的是右旋转,否则为左旋转
if (value < node.value){
rightRotate(parent);
}else if (value > node.value){
leftRotate(parent);
}
}
}
/**
* 左旋转
* @param node 旋转的父结点
*/
public void leftRotate(Node node){
Node rightNode = node.right;
// 旋转结点的左子结点给父结点的右子结点
node.right = rightNode.left;
// 父结点作为子结点的左子结点
rightNode.left = node;
}
/**
* 右旋转
* @param node
*/
public void rightRotate(Node node){
Node leftNode = node.left;
// 旋转结点的右子结点给父结点的左子结点
node.left = leftNode.right;
// 父结点作为子结点的右子结点
leftNode.right = node;
}
旋转变色案例应用
在上面结点为38的红黑中插入结点55。应用前面讲解到的变色后,红黑树结构如图:
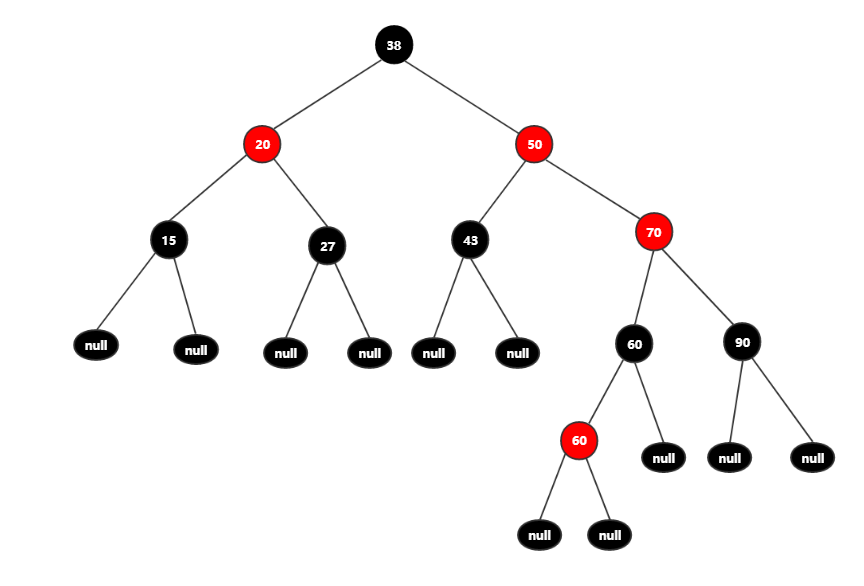
此时出现不满足红黑树特性(不允许连续两个结点都为红色),这时需要我们将结点50和结点38进行左旋转,得到如下图:

根结点50不符合红黑树特性(根结点必须为黑色),所以先将根结点变为黑色后。
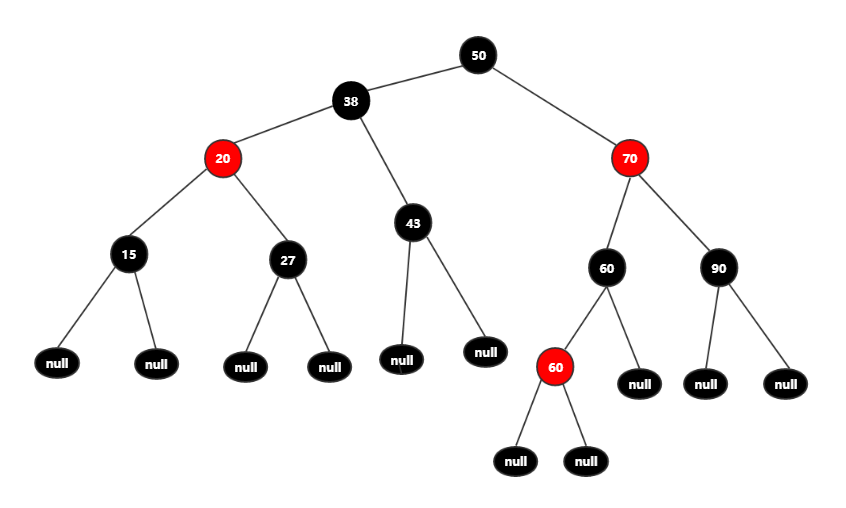
现在得到的红黑树,又出现违背(任一结点到叶子结点的每条路径上黑色结点数量都相等)特性,左树比右树多一个黑色结点,此时将38,20,15,27颜色改变。
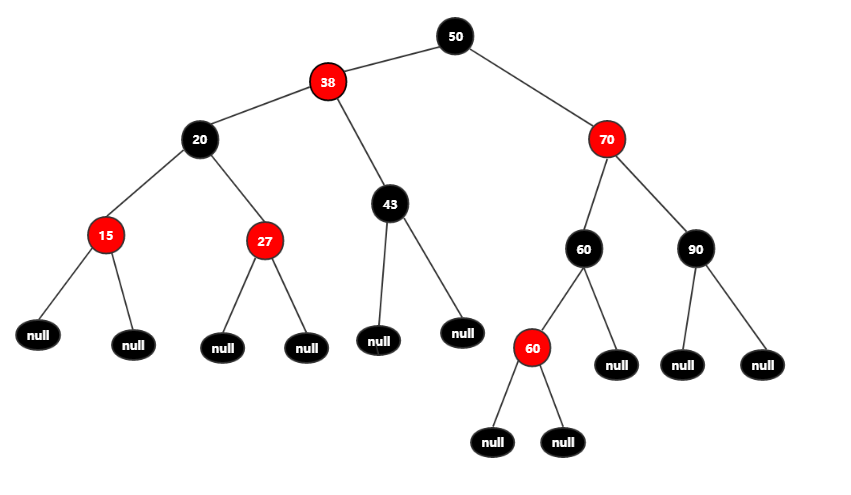
这里经过变色旋转完成了上面这课树的操作红黑树的调整。
由于代码篇幅较大,并没有将全部可能情况都考虑进来。相信理解了红黑树的对编码实现不是太大问题。
总结
红黑树的操作是基于普通二叉查找树上加了红黑树的特性,不管是插入还是删除操作,也就是在普通红黑树上进行旋转变色调整树结构,所以在理解红黑树的时候,主要把握旋转,变色,利用旋转变色来满足红黑树的特性,这也是红黑树的精华所在。懂得其原理和设计思想的话,应用到实际中解决问题确实是很不错的设计。当然,红黑树在实际的操作过程中是多变的,复杂的,要完全掌握还是要花点时间来研究的。
个人博客: https://ytao.top
我的公众号 ytao




