二叉树的实现

一.二叉排序树的结点类型

typedef int KeyType;
typedef struct node 
{       KeyType key;            	  //关键字项
　      InfoType data;          	  //其他数据域
        struct node *lchild,*rchild; 	  //左右孩子指针
}  BSTNode;

二.SearchBST(BSTNode *T,KeyType k)

伪代码

BSTNode *SearchBST(T,k)
{ 
      if (T为空 || T->key==k) 	            
            return T;                       //返回T，递归出口
      if (k<T->key)
    　   return SearchBST(T->lchild，k);   //在左子树中递归查找
      else
    　   return SearchBST(T->rchild，k);   //在右子树中递归查找
}

代码

BSTNode* SearchBST(BSTNode* T ,KeyType k)
{
    if (T == NULL || T->key == k)
        return T;
    if (k < T->key)
        return SearchBST(T->lchild,k);
    else
        return SearchBST(T->rchild,k);
}

三.InsertBST(BSTNode *&T，KeyType k)

伪代码

int InsertBST(T,k)	
{ 
     if (T为空)	 //原树为空， 新插入的记录为根结点
     {      创建一个新的key域为k的结点;
            return 1;
      }
      else if  (k==T->key) 	//存在相同关键字的结点，返回0
           return 0;
      else if (k<T->key) 
          return InsertBST(T->lchild，k);　	//插入到左子树中
      else  
          return InsertBST(p->rchild，k);  	//插入到右子树中
 }

代码

int InsertBST(BSTNode*& T,KeyType k)
{
    if (T == NULL)
    {
        T = new BSTNode;
        T->key = k;
        T->lchild = T->rchild = NULL;
        return 1;
    }
    else if (k == T->key)
        return 0;
    else if (k < T->key)
        return InsertBST(T->lchild,k);
    else
        return InsertBST(T->rchild,k);
}

四.CreatBST(KeyType A[]，int n)

伪代码

BSTNode *CreatBST(A[],n) //返回树根指针
{      BSTNode *T;
       T为空树;
       int i=0;
       while (i<n) 
       {    InsertBST(T，A[i]);  //将A[i]插入二叉排序树T中
　　         i++;
       }
       return T;       	    //返回建立的二叉排序树的根指针
}

代码

BSTNode* CreatBST(KeyType A[],int n)
{
    BSTNode* T = NULL;
    int i = 0;
    while (i < n)
    {
        InsertBST(T,A[i]);
        i++;
    }
    return T;
}

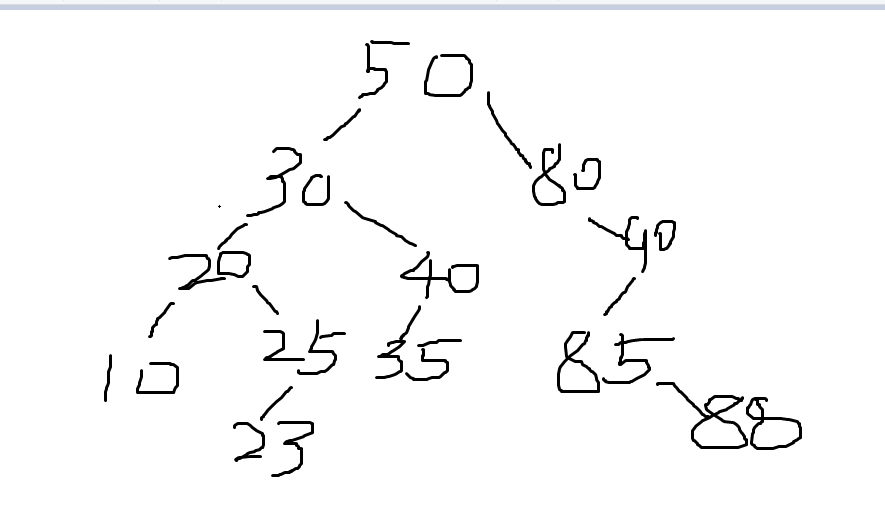
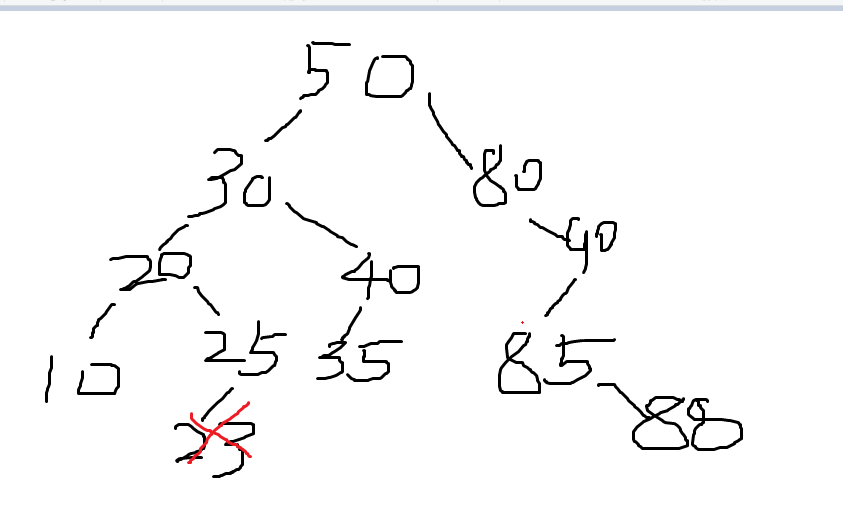
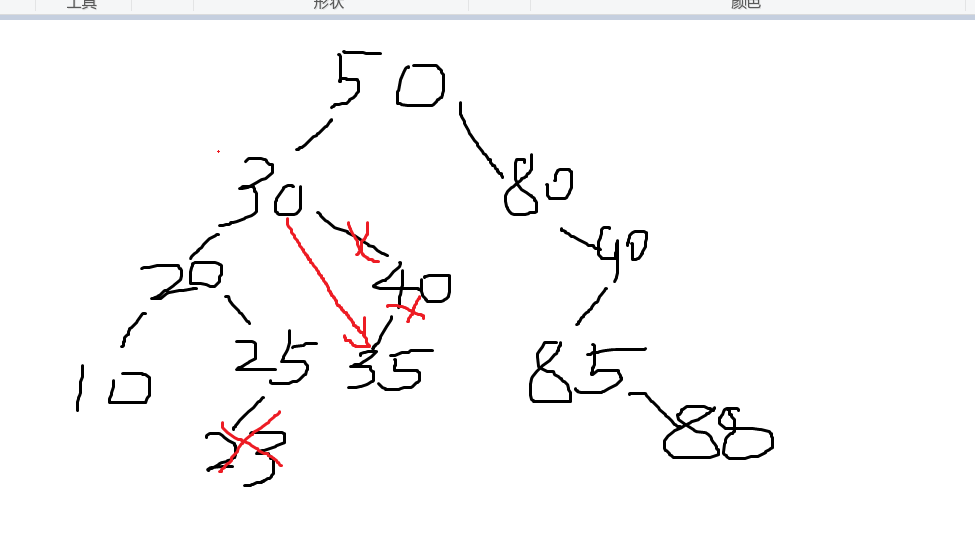
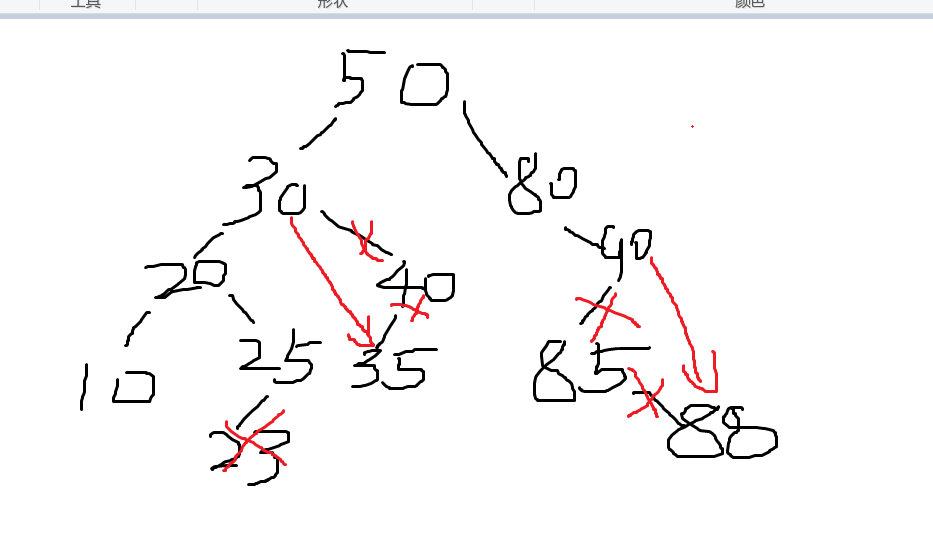
五.DeleteBST(BSTNode *&T，KeyType k)

伪代码

int DeleteBST(T,k)  //在bt删除关键字为k的结点
{ 
        if (T为空) return 0;	//空树删除失败
        else 
        {      if (k<T->key) return DeleteBST(T->lchild，k);	
                       //递归在左子树中删除为k的结点
	           else if (k>T->key) return DeleteBST(T->rchild，k);
	                   //递归在右子树中删除为k的结点
               else  
               {       Delete(T);    //调用Delete(T)函数删除*T结点
	                   return 1;
              }
      }
}

 void Delete(p)   	 //从二叉排序树中删除*p结点
{     BSTNode *q;
      if (p结点没有右子树)        	
      {    用其左孩子结点替换它
      }
      else if (p结点没有左子树)    	
      {    用其右孩子结点替换它
      }
      else Delete1(p，p->lchild);	
            //*p结点既没有左子树又没有右子树的情况
}

void Delete1(p,r)
  //当被删*p结点有左右子树时的删除过程
  {     BSTNode *q;
         if (r的右孩子不为空)
	   		Delete1(p，r->rchild);	//递归找*r的最右下结点
        else  		              //r指向最右下结点
        {   
        	用r结点替换p；
	   		删除r结点；
       }
  }

代码

int DeleteBST(BSTNode*& T,KeyType k)  
{
    if (T == NULL) return 0;	
    else
    {
        if (k < T->key) 
        	return DeleteBST(T->lchild,k);
        else if (k >T->key) 
        	return DeleteBST(T->rchild,k);
        else   
        {
            Delete(T);    
            return 1;
        }
    }
}
void Delete(BSTNode*& p)   	 
{
    BSTNode* q;
    if (p->rchild == NULL)        	
    {
        q = p; p = p->lchild;		
        free(q);
    }
    else if (p->lchild == NULL)    	
    {
        q = p; p = p->rchild;	
        free(q);
    }
    else Delete1(p,p->lchild);
}
void Delete1(BSTNode* p,BSTNode*& r)
{
    BSTNode* q;
    if (r->rchild != NULL)
        Delete1(p,r->rchild);	
    else  		              
    {
        p->key = r->key;  
        p->data = r->data;   
        q = r; r = r->lchild;          
        free(q); 	              
    }
}

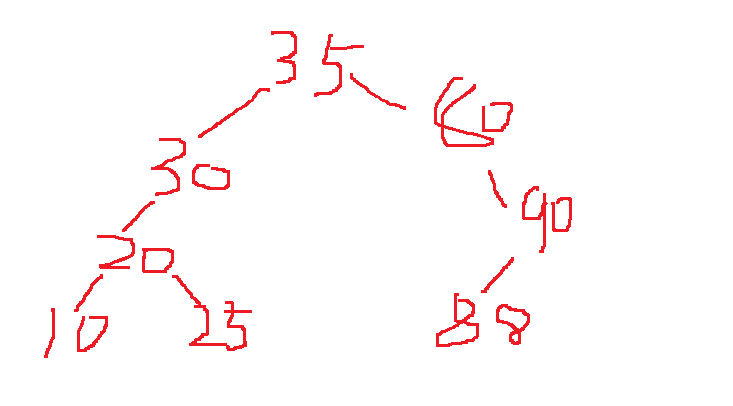
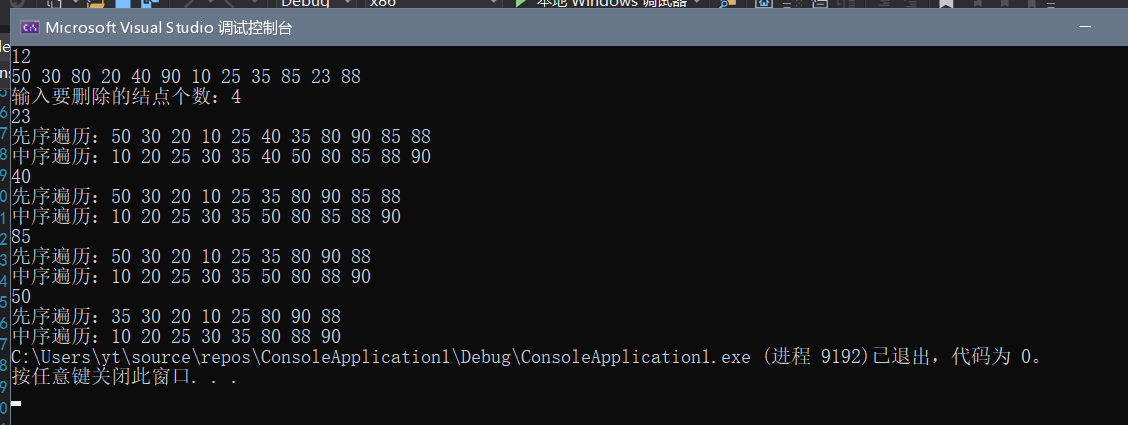
六.

随机生成包含100000个节点的BST，节点的值为证书其范围为[-300000,300000]，输出其树的高度。然后随机搜1000个数值，统计每次的ASL。

#include<iostream>
#include<cstdlib>
#include<ctime>
using namespace std;
typedef int KeyType;
typedef int InfoType;
typedef struct node
{
    KeyType key;            	  //关键字项
    InfoType data;          	  //其他数据域
    struct node* lchild, * rchild; 	  //左右孩子指针
}  BSTNode;
BSTNode* SearchBST(BSTNode* T ,KeyType k,int &count)
{
    if (T == NULL || T->key == k)
    {
        if (T!= NULL)
            count++;
        return T;
    }
        
    if (k < T->key)
    {
        count++;
        return SearchBST(T->lchild, k,count);
    }
    else
    {
        count++;
        return SearchBST(T->rchild, k,count);
    }
 }
        
int InsertBST(BSTNode*& T,KeyType k)
{
    if (T == NULL)
    {
        T = new BSTNode;
        T->key = k;
        T->lchild = T->rchild = NULL;
        return 1;
    }
    else if (k == T->key)
        return 0;
    else if (k < T->key)
        return InsertBST(T->lchild,k);
    else
        return InsertBST(T->rchild,k);
}
BSTNode* CreatBST(int n)
{
    BSTNode* T = NULL;
    int i = 0;
    int x;
    srand((unsigned int)time(NULL));
    while (i < n)
    {
        x = rand() * 10 % 300000 - 150000;
        InsertBST(T,x);
        i++;
    }
    return T;
}
void DestroyBST(BSTNode* bt)//销毁树
{
    if (bt != NULL)
    {
        DestroyBST(bt->lchild);
        DestroyBST(bt->rchild);
        delete bt;
    }
}
void InOrder(BSTNode* b)
{
    if (b != NULL)
    {
        InOrder(b->lchild);
        printf("%d ", b->key); 	//访问根结点
        InOrder(b->rchild);
    }
}
int GetHeight(BSTNode* BT)
{
    int lchilddep, rchilddep;
    if (BT == NULL) return(0); 	//空树的高度为0
    else
    {
        lchilddep = GetHeight(BT->lchild);
        //求左子树的高度为lchilddep
        rchilddep = GetHeight(BT->rchild);
        //求右子树的高度为rchilddep
        return(lchilddep > rchilddep) ? (lchilddep + 1) : (rchilddep + 1);
    }
}
int main()
{
    BSTNode* T;
    int n;
    int i;
    int count,sum=0;
    int height;
    cin >> n;
    srand((unsigned int)time(NULL));
    T=CreatBST( n);
    height=GetHeight(T);
    cout << "树的高度"<<height << endl;
    int a[1000];
    for (i = 0; i < 1000; i++)
    {
        a[i] = rand() * 10 % 300000 - 150000;
    }
    for (i = 0; i < 1000; i++)
    {
        count = 0;
        SearchBST(T, a[i], count);
        sum = sum + count;
    }
    cout << "ASL：";
    cout << sum / 1000;
    DestroyBST(T);
    return 0;
}

我通过许多次测试，树的平均高度为36，ASL的平均值为18。