Spark GraphX图计算快速入门
一.概述
GraphX是Spark中用于图形和图形并行计算的新组件。在较高的层次上，GraphX 通过引入新的Graph抽象来扩展Spark RDD：一个有向多重图，其属性附加到每个顶点和边上。为了支持图计算，GraphX公开了一组基本的操作符（例如， subgraph，joinVertices和 aggregateMessages），以及所述的优化的变体Pregel API。此外，GraphX包括越来越多的图形算法和 构建器集合，以简化图形分析任务。
二.入门
首先，需要将Spark和GraphX导入项目，如下所示：
import org.apache.spark._ import org.apache.spark.graphx._ // To make some of the examples work we will also need RDD import org.apache.spark.rdd.RDD
如果不使用Spark Shell，则还需要一个SparkContext。
三.属性图
GraphX的属性曲线图是一个有向多重图与连接到每个顶点和边的用户定义的对象。有向多重图是有向图，其中存在的多个平行边共享相同的源和目标顶点。支持平行边的功能简化了在相同顶点之间可能存在多个关系（例如，同事和朋友）的建模场景。每个顶点均由唯一的 64位长标识符（VertexId）设置密钥 。GraphX对顶点标识符没有施加任何排序约束。同样，边具有相应的源和目标顶点标识符。
在顶点（VD）和边（ED）类型上对属性图进行了参数化。这些是分别与每个顶点和边关联的对象的类型。
当顶点和边类型是原始数据类型（例如int，double等）时，GraphX可以优化它们的表示形式，方法是将它们存储在专用数组中，从而减少了内存占用量。
在某些情况下，可能希望在同一图形中具有不同属性类型的顶点。这可以通过继承来实现。例如，要将用户和产品建模为二部图，我们可以执行以下操作：
class VertexProperty() case class UserProperty(val name : String) extends VertexProperty case class ProductProperty(val name : String, val price : Double) extends VertexProperty // The graph might then have the type: var graph : Graph[VertexProperty, String] = null
像RDD一样，属性图是不可变的，分布式的和容错的。图的值或结构的更改是通过生成具有所需更改的新图来完成的。注意，原始图的实质部分（即不受影响的结构，属性和索引）在新图中被重用，从而降低了这种固有功能数据结构的成本。使用一系列顶点分区试探法在执行程序之间划分图。与RDD一样，发生故障时，可以在不同的计算机上重新创建图形的每个分区。
逻辑上，属性图对应于一对类型化集合（RDD），它们对每个顶点和边的属性进行编码。结果，图类包含访问图的顶点和边的成员：
class Graph[VD, ED] { val vertices: VertexRDD[VD] val edges: EdgeRDD[ED] }
Graph的类是VertexRDD[VD]和EdgeRDD[ED]的延伸，并且分别包含被优化的版本RDD[(VertexId, VD)]和RDD[Edge[ED]]。VertexRDD[VD]和EdgeRDD[ED]提供围绕图形计算，并利用内部优化内置附加功能。
属性图示例
假设我们要构造一个由GraphX项目中的各个协作者组成的属性图。顶点属性可能包含用户名和职业。我们可以用描述协作者之间关系的字符串注释边：
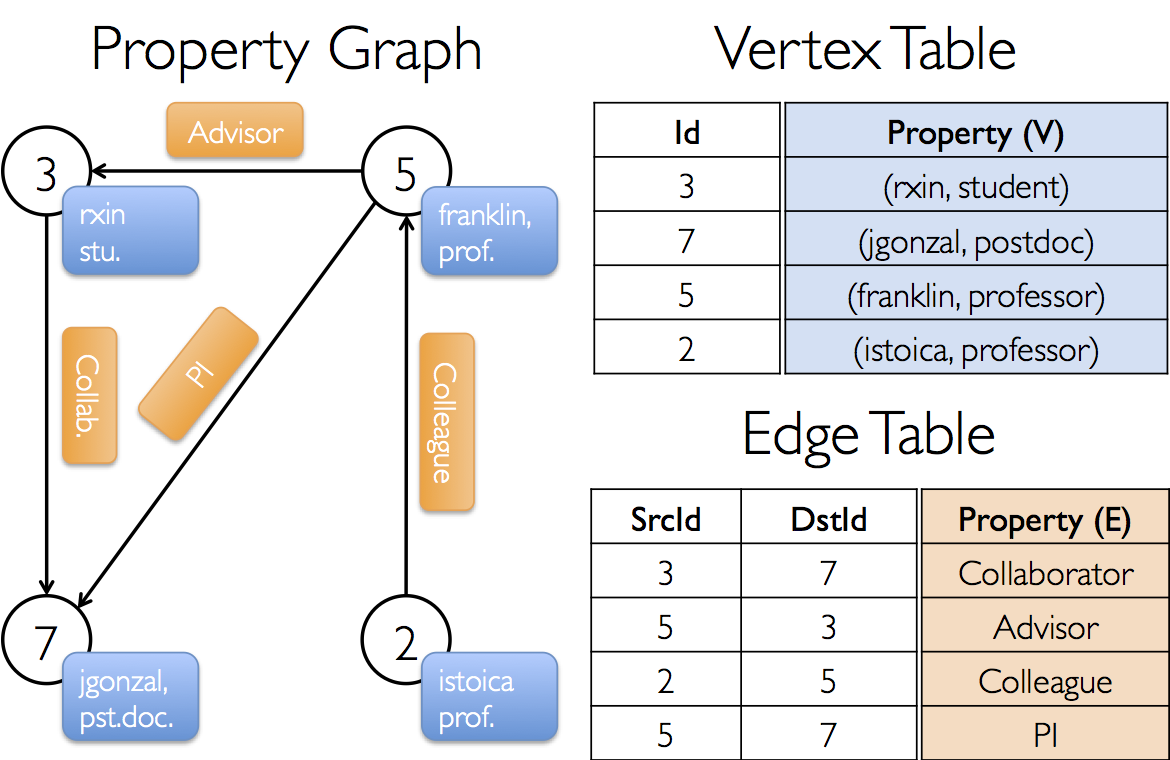
结果图将具有类型签名：
val userGraph: Graph[(String, String), String]
有多种方法可以从原始文件，RDD甚至是合成生成器构造属性图。最通用的方法是使用 Graph对象。例如，以下代码从RDD集合构造一个图形：
// Assume the SparkContext has already been constructed val sc: SparkContext // Create an RDD for the vertices val users: RDD[(VertexId, (String, String))] = sc.parallelize(Seq((3L, ("rxin", "student")), (7L, ("jgonzal", "postdoc")), (5L, ("franklin", "prof")), (2L, ("istoica", "prof")))) // Create an RDD for edges val relationships: RDD[Edge[String]] = sc.parallelize(Seq(Edge(3L, 7L, "collab"), Edge(5L, 3L, "advisor"), Edge(2L, 5L, "colleague"), Edge(5L, 7L, "pi"))) // Define a default user in case there are relationship with missing user val defaultUser = ("John Doe", "Missing") // Build the initial Graph val graph = Graph(users, relationships, defaultUser)
在上面的示例中，我们使用了Edge类。边具有srcId和dstId，分别对应于源和目标顶点标识符。另外，Edge类具有attr存储edge属性的成员。
我们可以分别使用graph.vertices 和graph.edges成员将图解构为相应的顶点和边视图。
val graph: Graph[(String, String), String] // Constructed from above // Count all users which are postdocs graph.vertices.filter {case (id, (name, pos)) => pos == "postdoc"}.count // Count all the edges where src > dst graph.edges.filter(e => e.srcId > e.dstId).count
请注意，graph.vertices返回VertexRDD[(String, String)]扩展了的 RDD[(VertexId, (String, String))]，因此我们使用scala case表达式来解构元组。另一方面，graph.edges返回一个EdgeRDD包含Edge[String]对象。我们还可以使用case类类型构造函数，如下所示：
graph.edges.filter {case Edge(src, dst, prop) => src > dst}.count
除了属性图的顶点和边视图外，GraphX还公开了一个三元组视图。三元组视图在逻辑上连接顶点和边属性，从而产生一个 RDD[EdgeTriplet[VD, ED]]包含EdgeTriplet类的实例。可以用以下SQL表达式表示此连接：
SELECT src.id, dst.id, src.attr, e.attr, dst.attr
FROM edges AS e LEFT JOIN vertices AS src, vertices AS dst
ON e.srcId = src.Id AND e.dstId = dst.Id
或图形化展示：
Graph的EdgeTriplet类扩展Edge通过添加类srcAttr和 dstAttr分别包含源和目的属性成员。我们可以使用图形的三元组视图来呈现描述用户之间关系的字符串集合。
val graph: Graph[(String, String), String] // Constructed from above // Use the triplets view to create an RDD of facts. val facts: RDD[String] = graph.triplets.map(triplet => triplet.srcAttr._1 + " is the " + triplet.attr + " of " + triplet.dstAttr._1) facts.collect.foreach(println(_))
四.图运算符
和RDD一样，属性图也具有一组基本运算符，例如，map、filter、reduceByKey等等，这些运算符采用用户定义的函数并生成具有转换后的特性和结构的新图。在属性图中定义了具有优化实现的核心运算符，并在其中定义了表示为核心运算符组成的便捷运算符。但是，由于使用了Scala隐式转换，Graph中的成员可以自动应用相应的运算符。例如，我们可以通过以下方法计算每个顶点（在Graph中定义）的度数：
val graph: Graph[(String, String), String] // Use the implicit GraphOps.inDegrees operator val inDegrees: VertexRDD[Int] = graph.inDegrees
Graph常用算子
/** Summary of the functionality in the property graph */ class Graph[VD, ED] { // Information about the Graph =================================================================== val numEdges: Long val numVertices: Long val inDegrees: VertexRDD[Int] val outDegrees: VertexRDD[Int] val degrees: VertexRDD[Int] // Views of the graph as collections ============================================================= val vertices: VertexRDD[VD] val edges: EdgeRDD[ED] val triplets: RDD[EdgeTriplet[VD, ED]] // Functions for caching graphs ================================================================== def persist(newLevel: StorageLevel = StorageLevel.MEMORY_ONLY): Graph[VD, ED] def cache(): Graph[VD, ED] def unpersistVertices(blocking: Boolean = false): Graph[VD, ED] // Change the partitioning heuristic ============================================================ def partitionBy(partitionStrategy: PartitionStrategy): Graph[VD, ED] // Transform vertex and edge attributes ========================================================== def mapVertices[VD2](map: (VertexId, VD) => VD2): Graph[VD2, ED] def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2] def mapEdges[ED2](map: (PartitionID, Iterator[Edge[ED]]) => Iterator[ED2]): Graph[VD, ED2] def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2] def mapTriplets[ED2](map: (PartitionID, Iterator[EdgeTriplet[VD, ED]]) => Iterator[ED2]) : Graph[VD, ED2] // Modify the graph structure ==================================================================== def reverse: Graph[VD, ED] def subgraph( epred: EdgeTriplet[VD,ED] => Boolean = (x => true), vpred: (VertexId, VD) => Boolean = ((v, d) => true)) : Graph[VD, ED] def mask[VD2, ED2](other: Graph[VD2, ED2]): Graph[VD, ED] def groupEdges(merge: (ED, ED) => ED): Graph[VD, ED] // Join RDDs with the graph ====================================================================== def joinVertices[U](table: RDD[(VertexId, U)])(mapFunc: (VertexId, VD, U) => VD): Graph[VD, ED] def outerJoinVertices[U, VD2](other: RDD[(VertexId, U)]) (mapFunc: (VertexId, VD, Option[U]) => VD2) : Graph[VD2, ED] // Aggregate information about adjacent triplets ================================================= def collectNeighborIds(edgeDirection: EdgeDirection): VertexRDD[Array[VertexId]] def collectNeighbors(edgeDirection: EdgeDirection): VertexRDD[Array[(VertexId, VD)]] def aggregateMessages[Msg: ClassTag]( sendMsg: EdgeContext[VD, ED, Msg] => Unit, mergeMsg: (Msg, Msg) => Msg, tripletFields: TripletFields = TripletFields.All) : VertexRDD[A] // Iterative graph-parallel computation ========================================================== def pregel[A](initialMsg: A, maxIterations: Int, activeDirection: EdgeDirection)( vprog: (VertexId, VD, A) => VD, sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)], mergeMsg: (A, A) => A) : Graph[VD, ED] // Basic graph algorithms ======================================================================== def pageRank(tol: Double, resetProb: Double = 0.15): Graph[Double, Double] def connectedComponents(): Graph[VertexId, ED] def triangleCount(): Graph[Int, ED] def stronglyConnectedComponents(numIter: Int): Graph[VertexId, ED] }
属性算子
与RDD运算符一样，属性图包含以下内容：
class Graph[VD, ED] { def mapVertices[VD2](map: (VertexId, VD) => VD2): Graph[VD2, ED] def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2] def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2] }
这些运算符中的每一个都会产生一个新图，其顶点或边属性由用户定义的map函数修改。
请注意，在各种情况下，图形结构均不受影响。这是这些运算符的关键功能，它允许生成的图重用原始图的结构索引。以下代码段在逻辑上是等效的，但第一个代码段不会保留结构索引，也不会从GraphX系统优化中受益：
val newVertices = graph.vertices.map {case (id, attr) => (id, mapUdf(id, attr))}
val newGraph = Graph(newVertices, graph.edges)
而是使用
mapVertices保留索引：
val newGraph = graph.mapVertices((id, attr) => mapUdf(id, attr))
这些运算符通常用于为特定计算初始化图或投影出不必要的属性。例如，给定一个以出度作为顶点属性的图，我们将其初始化为PageRank：
// Given a graph where the vertex property is the out degree val inputGraph: Graph[Int, String] = graph.outerJoinVertices(graph.outDegrees)((vid, _, degOpt) => degOpt.getOrElse(0)) // Construct a graph where each edge contains the weight // and each vertex is the initial PageRank val outputGraph: Graph[Double, Double] = inputGraph.mapTriplets(triplet => 1.0 / triplet.srcAttr).mapVertices((id, _) => 1.0)
结构算子
目前，GraphX仅支持一组简单的常用结构运算符。以下是基本结构运算符的列表。
class Graph[VD, ED] { def reverse: Graph[VD, ED] def subgraph(epred: EdgeTriplet[VD,ED] => Boolean, vpred: (VertexId, VD) => Boolean): Graph[VD, ED] def mask[VD2, ED2](other: Graph[VD2, ED2]): Graph[VD, ED] // 交集 def groupEdges(merge: (ED, ED) => ED): Graph[VD,ED] }
该reverse算子将返回逆转的所有边方向上的新图。例如，在尝试计算逆PageRank时，这将很有用。由于反向操作不会修改顶点或边的属性或更改边的数量，因此可以有效地实现它，而无需移动或复制数据。
该subgraph操作需要的顶点和边的谓词，并返回包含只有满足顶点谓词的顶点和满足边谓词边的曲线和满足顶点谓词连接顶点。subgraph 可以在多种情况下使用该运算符，以将图形限制在感兴趣的顶点和边或消除断开的链接。例如，在下面的代码中，我们删除了断开的链接：
// Create an RDD for the vertices val users: RDD[(VertexId, (String, String))] = sc.parallelize(Seq((3L, ("rxin", "student")), (7L, ("jgonzal", "postdoc")), (5L, ("franklin", "prof")), (2L, ("istoica", "prof")), (4L, ("peter", "student")))) // Create an RDD for edges val relationships: RDD[Edge[String]] = sc.parallelize(Seq(Edge(3L, 7L, "collab"), Edge(5L, 3L, "advisor"), Edge(2L, 5L, "colleague"), Edge(5L, 7L, "pi"), Edge(4L, 0L, "student"), Edge(5L, 0L, "colleague"))) // Define a default user in case there are relationship with missing user val defaultUser = ("John Doe", "Missing") // Build the initial Graph val graph = Graph(users, relationships, defaultUser) // Notice that there is a user 0 (for which we have no information) connected to users // 4 (peter) and 5 (franklin). graph.triplets.map( triplet => triplet.srcAttr._1 + " is the " + triplet.attr + " of " + triplet.dstAttr._1 ).collect.foreach(println(_)) // Remove missing vertices as well as the edges to connected to them val validGraph = graph.subgraph(vpred = (id, attr) => attr._2 != "Missing") // The valid subgraph will disconnect users 4 and 5 by removing user 0 validGraph.vertices.collect.foreach(println(_)) validGraph.triplets.map( triplet => triplet.srcAttr._1 + " is the " + triplet.attr + " of " + triplet.dstAttr._1 ).collect.foreach(println(_))
注意，在以上示例中，仅提供了顶点谓词。如果不设置顶点或边谓词
subgraph操作默认为true。
在mask操作通过返回包含该顶点和边，它们也在输入图形中发现曲线构造一个子图。可以与subgraph运算符结合使用， 以基于另一个相关图形中的属性来限制图形。例如，我们可能会使用缺少顶点的图来运行连接的组件，然后将答案限制为有效的子图。
// Run Connected Components val ccGraph = graph.connectedComponents() // No longer contains missing field // Remove missing vertices as well as the edges to connected to them val validGraph = graph.subgraph(vpred = (id, attr) => attr._2 != "Missing") // Restrict the answer to the valid subgraph val validCCGraph = ccGraph.mask(validGraph)
属性图的groupEdges操作在多重图中合并平行边（即，顶点对之间的重复边缘）。在许多数值应用中，可以将平行边添加 （合并了它们的权重）到单个边中，从而减小了图形的大小。
Join操作
在许多情况下，有必要将外部集合（RDD）中的数据与图形连接起来。例如，我们可能有想要与现有图形合并的额外用户属性，或者可能希望将顶点属性从一个图形拉到另一个图形。这些任务可以使用联接运算符来完成。下面我们列出了关键的联接运算符：
class Graph[VD, ED] { def joinVertices[U](table: RDD[(VertexId, U)])(map: (VertexId, VD, U) => VD) : Graph[VD, ED] def outerJoinVertices[U, VD2](table: RDD[(VertexId, U)])(map: (VertexId, VD, Option[U]) => VD2) : Graph[VD2, ED] }
Graph的joinVertices运算符与输入RDD顶点进行连接并返回通过应用用户定义获得的顶点属性的新图形。RDD中没有匹配值的顶点保留其原始值。
请注意，如果RDD对于给定的顶点包含多个值，则只会使用一个。因此，建议使用以下命令使输入RDD唯一，这也将对结果值进行预索引，以大大加快后续连接的速度。
val nonUniqueCosts: RDD[(VertexId, Double)] val uniqueCosts: VertexRDD[Double] = graph.vertices.aggregateUsingIndex(nonUnique, (a,b) => a + b) val joinedGraph = graph.joinVertices(uniqueCosts)( (id, oldCost, extraCost) => oldCost + extraCost)
除了将用户定义的函数应用于所有顶点并可以更改顶点属性类型外，其他outerJoinVertices行为与常规行为类似。由于并非所有顶点在输入RDD中都可能具有匹配值，因此该函数采用一种类型。例如，我们可以通过使用初始化顶点属性来为PageRank设置图形。
val outDegrees: VertexRDD[Int] = graph.outDegrees val degreeGraph = graph.outerJoinVertices(outDegrees){(id, oldAttr, outDegOpt) => outDegOpt match { case Some(outDeg) => outDeg case None => 0 // No outDegree means zero outDegree } }
虽然我们可以同样地写f(a)(b)，f(a,b)但这意味着对类型的推断b将不依赖a。结果，用户将需要为用户定义的函数提供类型注释：
val joinedGraph = graph.joinVertices(uniqueCosts,
(id: VertexId, oldCost: Double, extraCost: Double) => oldCost + extraCost)
邻里聚集
许多图形分析任务中的关键步骤是聚合有关每个顶点邻域的信息。例如，我们可能想知道每个用户拥有的关注者数量或每个用户的关注者平均年龄。许多迭代图算法（例如，PageRank，最短路径和连接的组件）反复聚合相邻顶点的属性（例如，当前的PageRank值，到源的最短路径以及最小的可到达顶点ID）。
为了提高性能，主要聚合运算符从更改
graph.mapReduceTriplets为graph.AggregateMessages。
汇总消息（aggregateMessages）
GraphX中的核心聚合操作为aggregateMessages。该运算符将用户定义的sendMsg函数应用于图形中的每个边三元组，然后使用该mergeMsg函数在其目标顶点处聚合这些消息。
class Graph[VD, ED] { def aggregateMessages[Msg: ClassTag]( sendMsg: EdgeContext[VD, ED, Msg] => Unit, mergeMsg: (Msg, Msg) => Msg, tripletFields: TripletFields = TripletFields.All) : VertexRDD[Msg] }
用户定义的sendMsg函数采用EdgeContext，将公开源和目标属性以及边属性和函数（sendToSrc和sendToDst），以将消息发送到源和目标节点。sendMsg可以认为是 map-reduce中的map函数。用户定义的mergeMsg函数接受两条发往同一顶点的消息，并产生一条消息。可以认为是map-reduce中的reduce函数。Graph的 aggregateMessages操作返回一个VertexRDD[Msg] ，包含发往每个顶点的聚合消息（类型的Msg）。未收到消息的顶点不包含在返回的VertexRDD中。
另外，aggregateMessages采用一个可选参数 tripletsFields，该参数指示访问哪些数据EdgeContext （即，源顶点属性，而不是目标顶点属性）。Graph的可能选项在tripletsFields中定义，TripletFields默认值为TripletFields.All，指示用户定义的sendMsg函数可以访问任何顶点。该tripletFields参数可用于限制GraphX仅访问部分顶点， EdgeContext允许GraphX选择优化的联接策略。例如，如果我们正在计算每个用户的关注者的平均年龄，则仅需要源字段，因此我们可以TripletFields.Src用来表明我们仅需要源字段。
在GraphX的早期版本中，我们使用字节码检查来推断
TripletFields，但是我们发现字节码检查有些不可靠，而是选择了更明确的用户控制。
在以下示例中，我们使用aggregateMessages运算符来计算每个用户的追随者的平均年龄。
package spark2.graphx import org.apache.log4j.{Level, Logger} import org.apache.spark.graphx.{Graph, VertexRDD} import org.apache.spark.graphx.util.GraphGenerators import org.apache.spark.sql.SparkSession object AggregateMessagesExample { Logger.getLogger("org").setLevel(Level.WARN) def main(args: Array[String]): Unit = { // Creates a SparkSession. val spark = SparkSession .builder .appName(s"${this.getClass.getSimpleName}") .master("local[2]") .getOrCreate() val sc = spark.sparkContext // 随机生成一个图 val graph: Graph[Double, Int] = GraphGenerators.logNormalGraph(sc, numVertices = 5).mapVertices((id, _) => id.toDouble) graph.triplets.collect.foreach(println) println("------------") // Compute the number of older followers and their total age val olderFollowers: VertexRDD[(Int, Double)] = graph.aggregateMessages[(Int, Double)]( triplet => { // Map Function if (triplet.srcAttr > triplet.dstAttr) { // Send message to destination vertex containing counter and age triplet.sendToDst((1, triplet.srcAttr)) } }, // Add counter and age (a, b) => (a._1 + b._1, a._2 + b._2) // Reduce Function ) olderFollowers.collect.foreach(println) println("===============") // Divide total age by number of older followers to get average age of older followers val avgAgeOfOlderFollowers: VertexRDD[Double] = olderFollowers.mapValues( (id, value) => value match {case (count, totalAge) => totalAge / count}) // Display the results avgAgeOfOlderFollowers.collect.foreach(println) // $example off$ spark.stop() } }
执行结果：
