Spark GraphX快速入门
一.概述
GraphX是Spark用于图形并行计算的新组件。在较高的层次上,GraphX通过引入一个新的Graph抽象来扩展Spark RDD:一个定向的多图,其属性附加到每个定点和边。为了支持图计算,GraphX公开了一组基本的操作符(子图,joinVertices和aggregateMessages),以及上述优化的变体API。此外,GraphX包括越来越多的图形算法和构建器集合,以简化图形分析任务。
二..属性图
GraphX的属性曲线图是一个有向多重图与连接到每个顶点边缘的用户定义对象。其可能有多个平行边共享相同的源和目标顶点。支持平行边的能力简化了在相同顶点之间存在多个关系的建模场景(例如:即使朋友又是同事)。每个顶点都是由唯一的64位长标识符【VertexId】设置秘钥。GraphX不对顶点标识符施加任何排序约束。同样,边具有相应的源和目标顶点标识符。
在顶点【VD】和边【ED】类型上对属性图进行了参数化。这些分别是与每个顶点和边关联的对象的类型。
当顶点和边类型是原始数据类型【例如:int, double等】时,GraphX可以优化它们的表示形式,方法是将它们存储在专用数组中,从而减少了内存占用量。
在某些情况下,可能希望同一图形中具有不同属性类型的顶点。这可以通过继承来实现。例如,要将用户和产品建模为二部图,可以执行以下操作:

与RDD一样,属性图是不可变,分布式和容错的。通过生成具有所需更改的新图来完成对图的值或结构的修改。原始图形的大部分(未影响的结构,属性和索引)在新图中被重用,从而降低了此固有功能数据结构的成本。使用一系列顶点分区试探法在执行程序之间划分图。与RDD一样,发生故障时,可以在不同的计算机上重新创建图形的每个分区。逻辑上,属性图对应于一对类型化集合【RDD】,它们对每个顶点和边的属性进行编码。结果,图类包含访问图的顶点和边的成员的类VertexRDD[VD]和EdgeRDD[ED]的延伸,并且被分别优化为RDD[(VertexId, VD)]和RDD[Edge[ED]]。

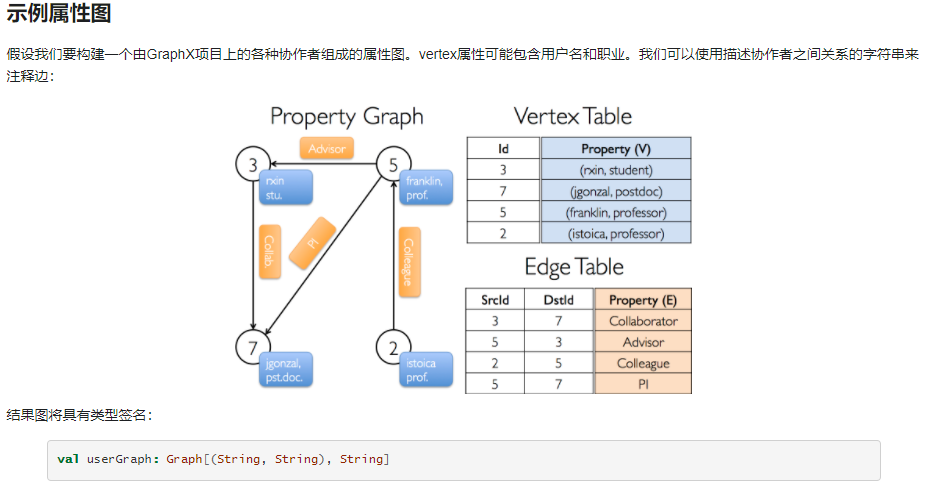
分别使用graph.vertices和graph.edges成员将图解析成相应的顶点和边视图。graph.vertices返回一个VertexRDD[(String, String)]扩展的RDD[(VertexId, (String, String))],graph.edges返回一个EdgeRDD,其包含Edge[String]的对象。
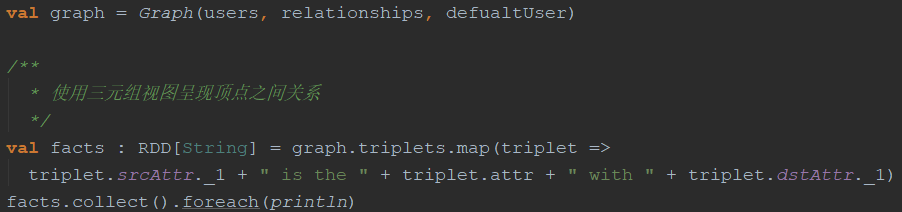
除了属性图的顶点和边视图外,GraphX还公开了一个三元组视图。三元组视图在逻辑上将顶点和边属性结合起来,从而产生一个RDD[EdgeTriplet[VD, ED]]包含EdgeTriplet类的实例。其图形化为:

EdgeTriplet类扩Edge通过添加类srcAttr和dstAttr分别包含源和目标属性成员。可以使用图形的三元组视图来呈现描述用户之间关系的字符串集合。
三.图运算符
正如RDDS有基本操作map,filter和reduceByKey等一样,图也有类似的函数,产生具有转化特性和结构的新图。已定义的具有优化实现的核心运算符如下:
这些运算符中的每一个都生成一个新图形,其顶点或边缘的属性由用户定义的map函数修改。
注意:在每种情况下,图形的结构都不会改变,这是这些运算符的关键特征,它允许结果图重用原始图的结构索引!
4.结构运算符
class Graph[VD, ED] {
// Information about the Graph
val numEdges: Long
val numVertices:Long
val inDegrees: VertexRDD[Int]
val outDegrees: VertexRDD[Int]
val degrees: VertexRDD[Int]
// Views of the graph as collections
val vertices: VertexRDD[VD]
val edges: EdgeRDD[ED]
val triplets: RDD[EdgeTriplet[VD,ED]]
//Functions for caching graphs
def persist(newLevel1:StorageLevel = StorageLevel.MEMORY_ONLY): Graph[VD, ED]//默认存储级别为MEMORY_ONLY
def cache(): Graph[VD, ED]
def unpersistVertices(blocking: Boolean = true): Graph[VD, ED]
// Change the partitioning heuristic
def partitionBy(partitionStrategy: PartitionStrategy)
// Transform vertex and edge attributes
def mapVertices[VD2](map: (VertexId, VD) => VD2): Graph[VD2, ED]
def mapEdges[ED2](map: Edge[ED] => ED2): Graph[VD, ED2]
def mapEdges[ED2](map: (PartitionID, Iterator[Edge[ED]]) => Iterator[ED2]): Graph[VD, ED2]
def mapTriplets[ED2](map: EdgeTriplet[VD, ED] => ED2): Graph[VD, ED2]
def mapTriplets[ED2](map: (PartitionID, Iterator[EdgeTriplet[VD, ED]]) => Iterator[ED2]): Graph[VD, ED2]
// Modify the graph structure def reverse: Graph[VD, ED] def subgraph(epred: EdgeTriplet[VD,ED] => Boolean,vpred: (VertexId, VD) => Boolean): Graph[VD, ED] def mask[VD2, ED2](other: Graph[VD2, ED2]): Graph[VD, ED] // 返回当前图和其它图的公共子图 def groupEdges(merge: (ED, ED) => ED): Graph[VD,ED]
// Join RDDs with the graph
def joinVertices[U](table: RDD[(VertexId, U)])(mapFunc: (VertexId, VD, U) => VD): Graph[VD, ED]
def outerJoinVertices[U, VD2](other: RDD[(VertexId, U)])(mapFunc: (VertexId, VD, Option[U]))
// Aggregate information about adjacent triplets
def collectNeighborIds(edgeDirection: EdgeDirection): VertexRDD[Array[VertexId]]
def collectNeighbors(edgeDirection: EdgeDirection): VertexRDD[Array[(VertexId, VD)]]
def aggregateMessages[Msg: ClassTag](sendMsg: EdgeContext[VD, ED, Msg] => Unit, merageMsg: (Msg, Msg) => Msg, tripletFields: TripletFields: TripletFields = TripletFields.All): VertexRDD[A]
//Iterative graph-parallel computation
def pregel[A](initialMsg: A, maxIterations: Int, activeDirection: EdgeDiection)(vprog: (VertexId, VD, A) => VD, sendMsg: EdgeTriplet[VD, ED] => Iterator[(VertexId, A)], mergeMsg: (A, A) => A): Graph[VD, ED]
// Basic graph algorithms
def pageRank(tol: Double, resetProb: Double = 0.15): Graph[Double, Double]
def connectedComponents(): Graph[VertexId, ED]
def triangleCount(): Graph[Int, ED]
def stronglyConnectedComponents(numIter: Int): Graph[VertexId, ED]
}
函数reverse将返回逆转所有边缘方向的新图。当尝试计算反向PageRank时,这可能会很有用。由于反向操作不会修改顶点或边缘属性或更改边数,因此可以有效的实现,而无需数据移动或复制。
在许多情况下,有必要将外部数据(RDD)与图形关联起来。
1 class Graph[VD, ED] { 2 def joinVertices[U](table: RDD[(VertexId, U)])(map: (VertexId, VD, U) => VD) 3 : Graph[VD, ED] 4 def outerJoinVertices[U, VD2](table: RDD[(VertexId, U)])(map: (VertexId, VD, Option[U]) => VD2) 5 : Graph[VD2, ED] 6 }
内连接(joinVertices)运算符连接输入RDD并返回通过用户定义关系关联的新图形。RDD中没有匹配的顶点保留原始值。
外连接(outerJoinVertices)运算符:因为并非所有的顶点在输入RDD中都具有匹配值,所以在不确定的时候可以采用该类型。
五.相邻聚集
许多图形分析任务中的关键步骤是汇总有关每个顶点邻域的信息。例如:我们可能想知道每个用户拥有的关注者数量或每个用户的关注者的平均年龄。许多迭代算法【例如:PageRank,最短路径和连接的组件】反复聚合相邻顶点的属性。为了提高性能,主要聚合运算符从graph.mapReduceTriplets更改为graph.AggregateMessage。
六.汇总消息【AggregateMessage】
GraphX中的核心聚合操作为aggregateMessage,该运算符将用户定义的sendMsg函数应用于图形的每个边三元组,然后使用该mergeMsg 函数在其目标顶点处聚合这些消息。
用户定义的sendMsg函数采用EdgeContext,将公开源和目标属性以及边缘属性和函数,以将消息发送到源和目标属性。可以将sendMsg视为mapReduce中的map函数。用户定义的mergeMsg函数接受两条发往同一顶点的消息,并产生一条消息。可以认为是mapReduce中的reduce函数。使用aggregateMessages返回一个VertexRDD[Msg]对象,该对象包含该聚合消息并将消息发往各个顶点。未收到消息的顶点不包含在返回的VertexRDD中。另外,aggregateMessage采用一个可选参数tripletsFields,该参数指示访问了哪些数据的EdgeContext,选项在tripletsFields中定义,TripletsFields默认值为TripletsFields.All,指示用户定义的sendMsg函数可以访问任何EdgeContext。tripletsFields参数可以设置只通知GraphX的一部分,EdgeContext从而允许GraphX选择优化的连接策略。例如:如果只需要源顶点数据,可以设置TripletsFields.Src表示我们仅需要源顶点信息。
在GraphX的早期版本中,使用字节码检查来推断TripletsFields,但是我们发现字节码检查稍微不靠谱,因而选择了更明确的用户控制。
代码实战例子参考:https://www.cnblogs.com/yszd/p/11726921.html
七.缓存
Spark默认情况下RDD不保留在内存中。为避免重新计算,可以在多次使用时显式缓存。GraphX中的图也是一样。多次使用图时,确保先调用Graph.cache()。
在迭代计算中,为了获得最佳性能,也可能需要取消缓存。默认情况下,缓存的RDD和图保存在内存中,直到内存压力迫使它们按照LRU【最近最少使用页面交换算法】逐渐从内存中移除。对于迭代计算,先前的中间结果将填满内存。经过它们最终被移除内存,但存储在内存中的不必要数据将减慢垃圾回收速度。因此,一旦不再需要中间结果,取消缓存中间结果将更加有效。这涉及在每次迭代中实现缓存图或RDD,取消缓存其他所有数据集,并仅在以后的迭代中使用实现的数据集。但是,由于图是有多个RDD组成的,因此很难正确地取消持久化。对于迭代计算,建议使用Pregel API,它可以正确地保留中间结果。
八.Pregel API
图是固有的递归数据结构,因为定点的属性取决于其自身的属性,又取决于其相邻节点的属性。这导致许多图形算法会迭代重新计算每个顶点的属性,直到到达指定条件为止。其中,GraphX实现了基于Pregel API的变体。在较高层次上,GraphX中的Pregel运算符是受图拓扑约束的大量同步并行消息传递的抽象。Tregel运算符在一系列超级步骤中执行,其中定点从上一个超级步骤接收入栈消息的总和,计算顶点属性的新值,然后在下一个超级步骤中将消息发送到相邻的顶点。与Pregel不同,消息是根据边三元组并行计算的,并且消息计算可以访问源顶点和目标顶点属性。在超级步骤中会跳过未收到消息的顶点。当没有消息剩余时,Pregel运算符终止迭代并返回最终结果图。
注意,与标准的Pregel实现不同,GraphX中的顶点只能将消息发送到相邻的顶点,并且使用用户定义的消息传递功能并行完成消息的构造。这些限制允许在GraphX中进行其它优化。Pregel使用了两个参数列表,第一个参数列表包含配置参数,包含初始消息,最大迭代次数以及发送消息的边方向。第二个参数列表包含用户定义的函数,这些函数用于接收消息【顶点程序vprog】、计算消息【sendMsg】以及组合消息【mergeMsg】。



