高斯消元

首先，应用为解决一次n元方程组

1、将系数与答案存入矩形，下图即为转换前后

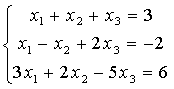
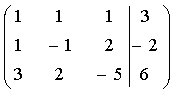
 2、消元就要消到对角线系数为1，其他都为0，此时最右列为此行此列未知数的解

清楚思路，开始操作

1、循环到i行，从此行向下找i列不为0的一行，并与他交换，确保i行i列不为0才能除到1。当然若找不到的话，即有一列全为0，此未知数无解

2、将i列的其他元素减成0，当然要用（i，i）这一系数为1的元素减。确定减去i组方程的倍数，即（j，i）。/*就是加减消元法*/j行所有元素减去倍数乘i行对应元素

其实这种对角线形式是高斯-约旦消元法，而高斯消元法则转化成上三角矩形，再反代 

 

现在谈谈“如何判断解的情况”

由一元一次方程ax=b

唯一解：a≠0

无数解：a=b=0

无解：a=0，b≠0

在上个代码系数化为1中，显然只能判断（a=0）？，无法确定（b=0）？，也就是只知道是否有唯一解

很简单，我们可以不强求系数为1，保留原系数，化为ax=b

在选择i与哪一行交换时，寻找系数绝对值最大的一行，保证精度

这样i就不能表示i行保留哪个未知数，需要id【i】和line记录

遇到x的系数全部为0，直接跳过这一未知数

最后再给剩下主元随便分配一个剩下的方程

判断解时，先看是否有解，再看是否有无穷解。易知方程组中x₁有无穷解，x₂无解，此方程组实际上无解

代码

const double eps=1e-8;
line=1;
for(int i=1;i<=n;++i){
    int _max=line;
    for(int j=line+1;j<=n;++j)
        if(fabs(a[j][i])>fabs(a[_max][i])  _max=j;
    if(!a[_max][i])  continue;
    for(int j=1;j<=n+1;++j)  swap(a[_max][j],a[line][j]);
    for(int j=1;j<=n;++j){
        if(j==line)  continue;
        double ki=1.0*a[j][i]/a[line][i];
        for(int k=i+1;k<=n+1;++k)  a[j][k]-=a[line][k]*ki;
    }id[i]=line++;    
}
for(int i=1;i<=n;++i)
    if(!id[i])  id[i]=line++;
for(int i = 1; i <= n; ++i) if(!a[id[i]][i] && a[id[i]][n+1]){puts("-1"); return 0;}
for(int i = 1; i <= n; ++i) if(!a[id[i]][i] && !a[id[i]][n+1]) {puts("0"); return 0;}
for(int i = 1; i <= n; ++i) printf("x%d=%.2lf\n", i, fabs(a[id[i]][n+1] / a[id[i]][i]) < eps ? 0 : a[id[i]][n+1] / a[id[i]][i])

inline int power(int a,int b){
    int res=1;
    while(b){
        if(b&1)  res=res*a%mod;
        a=a*a%mod;b>>=1;
    }return res;
}inline void GAUSS(){
    for(int i=1;i<=n;++i)
        for(int j=1;j<=n;++j){
            if(j==i)  continue;
            int ki=a[j][i]*power(a[i][i],mod-2)%mod;
            for(int k=i+1;k<=n+1;++k)  (a[j][k]-=a[i][k]*ki)%=mod;
        }   
}

inline int GAUSS(){
    int res=1;
    for(int i=1;i<=n;++i){
        for(int j=i+1;j<=n;++j){
            while(f[i][i]){
                t=f[j][i]/f[i][i];
                for(int k=i;k<=n;++k)
                    f[j][k]=(f[j][k]-t*f[i][k]%mod)%mod;
                swap(f[i],f[j]);res=-res;
            }swap(f[i],f[j]);res=-res;
        }res=res*f[i][i]%mod;
    }return (res+mod)%mod;
}