hiho一下 第四十九周 题目1 : 欧拉路·一【无向图 欧拉路问题】
题目1 : 欧拉路·一
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
小Hi和小Ho最近在玩一个解密类的游戏,他们需要控制角色在一片原始丛林里面探险,收集道具,并找到最后的宝藏。现在他们控制的角色来到了一个很大的湖边。湖上有N个小岛(编号1..N),以及连接小岛的M座木桥。每座木桥上各有一个宝箱,里面似乎装着什么道具。
湖边还有一个船夫,船夫告诉主角。他可以载着主角到任意一个岛上,并且可以从任意一个岛上再载着主角回到湖边,但是主角只有一次来回的机会。同时船夫告诉主角,连接岛屿之间的木桥很脆弱,走过一次之后就会断掉。
因为不知道宝箱内有什么道具,小Hi和小Ho觉得如果能把所有的道具收集齐肯定是最好的,那么对于当前岛屿和木桥的情况,能否将所有道具收集齐呢?
举个例子,比如一个由6个小岛和8座桥组成的地图:
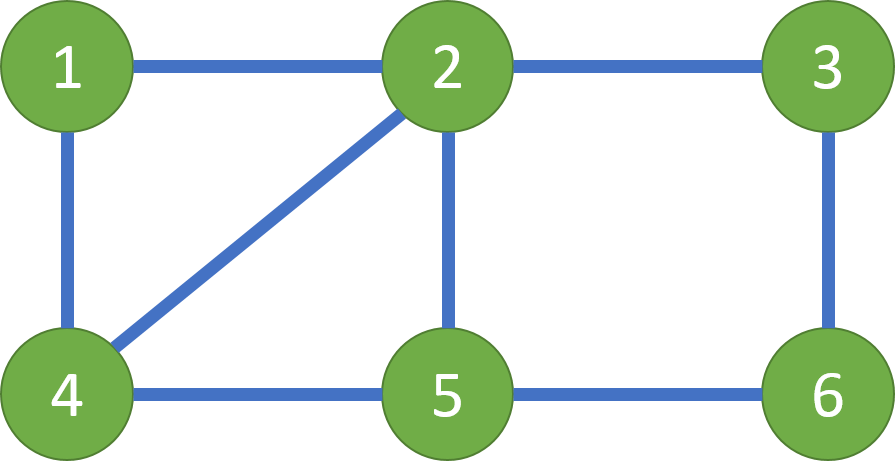
主角可以先到达4号小岛,然后按照4->1->2->4->5->6->3->2->5的顺序到达5号小岛,然后船夫到5号小岛将主角接回湖边。这样主角就将所有桥上的道具都收集齐了。
输入
第1行:2个正整数,N,M。分别表示岛屿数量和木桥数量。1≤N≤10,000,1≤M≤50,000
第2..M+1行:每行2个整数,u,v。表示有一座木桥连接着编号为u和编号为v的岛屿,两个岛之间可能有多座桥。1≤u,v≤N
输出
第1行:1个字符串,如果能收集齐所有的道具输出“Full”,否则输出”Part”。
- 样例输入
-
6 8 1 2 1 4 2 4 2 5 2 3 3 6 4 5 5 6
- 样例输出
-
Full
算法分析:这道题目就是让你画一个一笔画,刚好经过所有的边一次即可,是关于欧拉路的问题。简单的把欧拉路径分一下类(基于无向
图):
1). 欧拉回路:图G的一个回路,若它恰通过图G中每条边仅一次,则称该回路为欧拉回路。(起点、终点相同)
解法:图G连通+度数为奇数的点的个数为0.
2). 具有欧拉回路的图成为欧拉图。
3). 欧拉图的变形:就是可以不会到原来的起点,但是仍要经历所有的边各一次,也就是所谓的一笔画问题。
解法:图G连通+度数为奇数的点的个数为2.一个是起点,一个是终点。
本题目中有提到说:两个点之间可能存在多条边,注意即使是存在多条变,每条边也都要遍历到才能满足要求。也就是,只要有边,该边
两个端点对应的节点的度数就要累加。
代码:#include <stdio.h> #include <string.h> #include <stdlib.h> #include <ctype.h> #include <math.h> #include <iostream> #include <string> #include <stack> #include <vector> #include <set> #include <queue> #include <algorithm> #define LL long long int #define N 10000+10 using namespace std; int n, m; //1≤N≤10000 1≤M≤50000 //欧拉路的判定(不是欧拉回路) //因为可以不必回到起点, 所以是欧拉路的变形 //1)必须是连通图 2)奇数度的点的个数必须为2 unsigned int in[N]; vector<int>qm[N]; bool vis[N]; bool dfs(int u) { vis[u]=true; for(int i=0; i<qm[u].size(); i++) { if(vis[qm[u][i]]==false ) { vis[qm[u][i]]=true; dfs(qm[u][i]); } } } int main() { scanf("%d %d", &n, &m); int i, j; memset(in, 0, sizeof(in)); for(i=0; i<=n; i++) qm[i].clear(); int u, v; for(i=0; i<m; i++){ scanf("%d %d", &u, &v ); qm[u].push_back(v); qm[v].push_back(u); in[u]++; in[v]++; } memset(vis, false, sizeof(vis)); dfs(1); bool flag=true; for(i=1; i<=n; i++){ if(vis[i]==false){ flag=false; break; } } int cnt=0; for(i=1; i<=n; i++) { if(in[i]%2==1 ) cnt++; } if(flag==true && (cnt==2 || cnt==0)) printf("Full\n"); else printf("Part\n"); return 0; }静态数组模拟:
注意:存储边的数组要开大一些,并不是开m条边的大小,会RE的,需要开更大,因为是双向边。
代码:
#include <stdio.h> #include <string.h> #include <stdlib.h> #include <ctype.h> #include <math.h> #include <iostream> #include <string> #include <algorithm> #define LL long long int #define N 10000+100 #define M 60000+100 using namespace std; int n, m; //1≤N≤10000 1≤M≤50000 //欧拉路的判定(不是欧拉回路) //因为可以不必回到起点, 所以是欧拉路的变形 //1)必须是连通图 2)奇数度的点的个数必须为2 unsigned int in[N]; bool vis[N]; int edgecnt; int head[N]={0}; int p[M]; int Next[M]={0}; void addedge(int u, int v) { ++edgecnt; p[edgecnt]=v; Next[edgecnt]=head[u]; head[u]=edgecnt; } bool dfs(int u) { int i; for(i=head[u]; i; i=Next[i]) { if(vis[p[i]]==false ) { vis[p[i]]=true; dfs(p[i]); } } } int main() { scanf("%d %d", &n, &m); int i, j; memset(in, 0, sizeof(in)); int u, v; edgecnt=0; for(i=0; i<m; i++){ scanf("%d %d", &u, &v ); addedge(u, v); addedge(v, u); in[u]++; in[v]++; } memset(vis, false, sizeof(vis)); vis[1]=true; dfs(1); bool flag=true; for(i=1; i<=n; i++){ if(vis[i]==false){ flag=false; break; } } int cnt=0; for(i=1; i<=n; i++) { if(in[i]%2==1 ) cnt++; } if(flag==true && (cnt==2 || cnt==0)) printf("Full\n"); else printf("Part\n"); return 0; }这是是十佳代码里的最短的代码,居然和我写的代码一样的算法实现,吓坏我了~~~
#include<cstdio> int d[10001],N,M,v; main() { for(scanf("%d%d",&N,&M); M--; d[*d]++,d[v]++) scanf("%d%d",d,&v); for(; N;)M+=d[N--]&1; puts(M>2?"Part":"Full"); }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号