POJ 1330 Nearest Common Ancestors 【最近公共祖先LCA算法+Tarjan离线算法】
Nearest Common Ancestors
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 20715 | Accepted: 10910 |
Description
A rooted tree is a well-known data structure in computer science and engineering. An example is shown below:
![]()
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
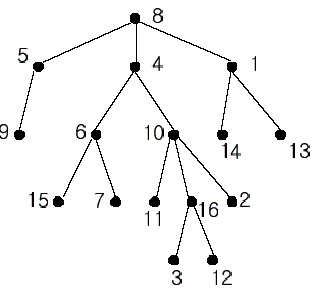
In the figure, each node is labeled with an integer from {1, 2,...,16}. Node 8 is the root of the tree. Node x is an ancestor of node y if node x is in the path between the root and node y. For example, node 4 is an ancestor of node 16. Node 10 is also an ancestor of node 16. As a matter of fact, nodes 8, 4, 10, and 16 are the ancestors of node 16. Remember that a node is an ancestor of itself. Nodes 8, 4, 6, and 7 are the ancestors of node 7. A node x is called a common ancestor of two different nodes y and z if node x is an ancestor of node y and an ancestor of node z. Thus, nodes 8 and 4 are the common ancestors of nodes 16 and 7. A node x is called the nearest common ancestor of nodes y and z if x is a common ancestor of y and z and nearest to y and z among their common ancestors. Hence, the nearest common ancestor of nodes 16 and 7 is node 4. Node 4 is nearer to nodes 16 and 7 than node 8 is.
For other examples, the nearest common ancestor of nodes 2 and 3 is node 10, the nearest common ancestor of nodes 6 and 13 is node 8, and the nearest common ancestor of nodes 4 and 12 is node 4. In the last example, if y is an ancestor of z, then the nearest common ancestor of y and z is y.
Write a program that finds the nearest common ancestor of two distinct nodes in a tree.
Input
The
input consists of T test cases. The number of test cases (T) is given in
the first line of the input file. Each test case starts with a line
containing an integer N , the number of nodes in a tree,
2<=N<=10,000. The nodes are labeled with integers 1, 2,..., N.
Each of the next N -1 lines contains a pair of integers that represent
an edge --the first integer is the parent node of the second integer.
Note that a tree with N nodes has exactly N - 1 edges. The last line of
each test case contains two distinct integers whose nearest common
ancestor is to be computed.
Output
Print exactly one line for each test case. The line should contain the integer that is the nearest common ancestor.
Sample Input
2 16 1 14 8 5 10 16 5 9 4 6 8 4 4 10 1 13 6 15 10 11 6 7 10 2 16 3 8 1 16 12 16 7 5 2 3 3 4 3 1 1 5 3 5
Sample Output
4
3
题目分析:T组数据,每组有n个节点,n-1条边,所以必定会是一棵树。每组输入的最后一行是两个点u, v。问你u和v的最近公共祖先是谁?
Tanjan离线算法。
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <math.h>
#include <vector>
#include <algorithm>
#define N 10000+10
using namespace std;
int n; int s, e;
vector<int>q[N];
int fa[N];
bool vis[N];
bool root[N];//标记该点是不是根节点
int findset(int x) //压缩路径并查集
{
return fa[x]!=x?fa[x]=findset(fa[x]):x;
}
void LCA(int u)
{
for(int i=0; i<q[u].size(); i++)
{
LCA(q[u][i]);
if(findset(u) != findset(q[u][i]))
{
fa[fa[q[u][i]]] = fa[u]; //合并
}
}
vis[u]=true;
if(u==s && vis[e]==true )
{
printf("%d\n", findset(e));
return ;
}
if(u==e && vis[s]==true )
{
printf("%d\n", findset(s));
return ;
}
}
int main()
{
int t;
scanf("%d", &t);
int i, j, k;
int u, v;
while(t--)
{
scanf("%d", &n); //n个节点
//初始化
for(i=0; i<=n; i++){
q[i].clear();
fa[i]=i; //将父亲节点设为自己
root[i]=true;
vis[i]=false; //标记未访问
}
for(i=0; i<n-1; i++)
{
scanf("%d %d", &u, &v); //u是v的父亲节点
q[u].push_back(v);
root[v]=false;
}
scanf("%d %d", &s, &e);
for(i=1; i<=n; i++)
{
if(root[i]==true )//该点是根节点
{
LCA(i); //进行LCA一次离线算法
break;
}
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号