Hihocoder #1077 : RMQ问题再临-线段树(线段树:结构体建树+更新叶子往上+查询+巧妙使用father[]+线段树数组要开大4倍 *【模板】)
#1077 : RMQ问题再临-线段树
时间限制:10000ms
单点时限:1000ms
内存限制:256MB
描述
上回说到:小Hi给小Ho出了这样一道问题:假设整个货架上从左到右摆放了N种商品,并且依次标号为1到N,每次小Hi都给出一段区间[L, R],小Ho要做的是选出标号在这个区间内的所有商品重量最轻的一种,并且告诉小Hi这个商品的重量。但是在这个过程中,可能会因为其他人的各种行为,对 某些位置上的商品的重量产生改变(如更换了其他种类的商品)。
小Ho提出了两种非常简单的方法,但是都不能完美的解决。那么这一次,面对更大的数据规模,小Ho将如何是好呢?
输入
每个测试点(输入文件)有且仅有一组测试数据。
每组测试数据的第1行为一个整数N,意义如前文所述。
每组测试数据的第2行为N个整数,分别描述每种商品的重量,其中第i个整数表示标号为i的商品的重量weight_i。
每组测试数据的第3行为一个整数Q,表示小Hi总共询问的次数与商品的重量被更改的次数之和。
每组测试数据的第N+4~N+Q+3行,每行分别描述一次操作,每行的开头均为一个属于0或1的数字,分别表示该行描述一个询问和描述一次商品的重 量的更改两种情况。对于第N+i+3行,如果该行描述一个询问,则接下来为两个整数Li, Ri,表示小Hi询问的一个区间[Li, Ri];如果该行描述一次商品的重量的更改,则接下来为两个整数Pi,Wi,表示位置编号为Pi的商品的重量变更为Wi
对于100%的数据,满足N<=10^6,Q<=10^6, 1<=Li<=Ri<=N,1<=Pi<=N, 0<weight_i, Wi<=10^4。
输出
对于每组测试数据,对于每个小Hi的询问,按照在输入中出现的顺序,各输出一行,表示查询的结果:标号在区间[Li, Ri]中的所有商品中重量最轻的商品的重量。
- 样例输入
-
10 3655 5246 8991 5933 7474 7603 6098 6654 2414 884 6 0 4 9 0 2 10 1 4 7009 0 5 6 1 3 7949 1 3 1227
- 样例输出
-
2414 884 7474
![]()
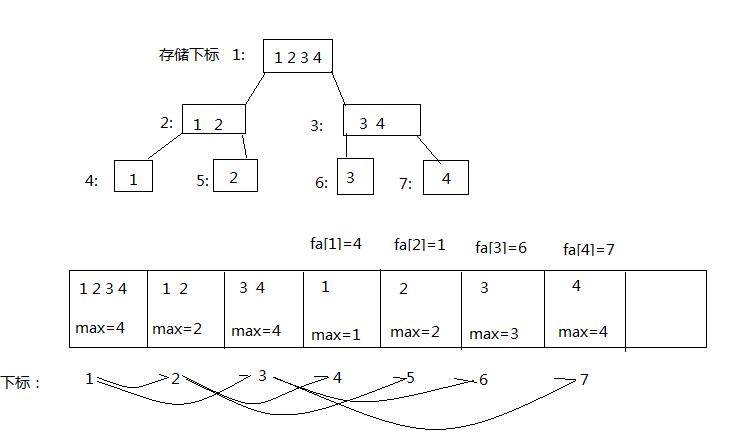
上面是我自己制作的简单的线段树的存储结构图
线段树的基础题,考的是线段树的数据结构实现。不讲算法
代码:#include <stdio.h> #include <string.h> #include <math.h> #include <iostream> #include <string> #include <algorithm> using namespace std; struct node { int ll; int rr; int mm; }q[4000010]; int fa[1000002]; void Build_ST(int i, int ll, int rr ) { q[i].ll=ll; q[i].rr=rr; q[i].mm=210000000; if(ll == rr ) // { fa[ll] = i; // return ; } Build_ST(i*2, ll, (ll+rr)/2 ); Build_ST(i*2+1, (ll+rr)/2+1, rr ); } void update_ST(int ri) //自下向上更新 输入的是底层节点的编号 { if(ri==1) { return ; //表示该底层节点是根节点 修改完成 返回 } //如果不是根节点 就一直往上修改 直到修改到根节点 int fi; // fi=ri/2; q[fi].mm = min( q[fi*2].mm, q[fi*2+1].mm ); //此处必须写成fi*2和fi*2+1的形式,因为整数除法精度问题,写成ri和ri+1会错的 update_ST(ri/2); } int Min; void query(int i, int ll, int rr ) { if(q[i].ll==ll && q[i].rr==rr )// { Min= min(Min, q[i].mm ); return ; } i=i<<1; if(ll<=q[i].rr ) { if(rr<=q[i].rr ) { query(i, ll, rr); } else { query(i, ll, q[i].rr ); } } i=i+1; if(rr>=q[i].ll ) { if(ll>=q[i].ll ) { query(i, ll, rr ); } else { query(i, q[i].ll, rr ); } } } int main() { int n, m; scanf("%d", &n); Build_ST(1, 1 , n);// int i, j; int dd; for(i=1; i<=n; i++) { scanf("%d", &dd ); q[fa[i]].mm = dd; update_ST(fa[i]); } scanf("%d", &m); int pos, num; int left, right; for(j=0; j<m; j++ ) { scanf("%d", &dd); if(dd==0) //xun wen { scanf("%d %d", &left, &right ); Min=210000000; query(1, left, right ); printf("%d\n", Min ); } else if(dd==1) { scanf("%d %d", &pos, &num ); //因为题目的原因,一定修改的是某个叶子节点的信息 q[fa[pos]].mm=num; update_ST(fa[pos]); } } return 0; }2015/8/18 重新写了
#include <stdio.h> #include <stdlib.h> #include <string.h> #include <ctype.h> #include <math.h> #include <queue> #include <iostream> #include <algorithm> #define INF 0x3f3f3f3f using namespace std; struct node { int ll, rr; int mm;//保存最大值 }q[4000000+10]; int fa[1000000+2]; /* 线段树是一种树状的数据结构,但在算法的实现过程中, 用的是一维结构体数组来模拟的, */ void Build(int i, int ll, int rr) { q[i].ll=ll; q[i].rr=rr;//当前线段节点的左右区间 q[i].mm=INF; if(ll==rr){ fa[ll]=i; return; }//如果当前的是叶子节点 //fa[]记录下了每个叶子节点的存储位置 Build(i*2, ll, (ll+rr)/2); Build(i*2+1, (ll+rr)/2+1, rr); } //往下递归两个儿子节点 void update(int ri) { if(ri==1){ return ; }//到达根节点 修改完成返回 int fi=ri/2; q[fi].mm=min(q[fi*2].mm, q[fi*2+1].mm); update(ri/2); } int Min; void query(int i, int ll ,int rr) { if(q[i].ll==ll&&q[i].rr==rr){ Min=min(Min, q[i].mm); return; }// i=i*2; if(ll<=q[i].rr){//在这个子节点有范围 if(rr<=q[i].rr){ query(i, ll, rr); }else{ query(i, ll, q[i].rr); } } i=i+1; if(rr>=q[i].ll){ if(ll>=q[i].ll ){ query(i, ll, rr); }else{ query(i, q[i].ll, rr); } } } int main() { int n, m;// scanf("%d", &n); Build(1,1,n); int i, j, cur; for(i=1; i<=n; i++){ scanf("%d", &cur); q[fa[i]].mm=cur; update(fa[i]); }//fa[i]是叶子节点的下标位置 scanf("%d", &m);//m次操作 int left, right; int pos, num; for(i=0; i<m; i++){ scanf("%d", &cur); if(cur==0){//询问区间最小值 scanf("%d %d", &left, &right); Min=INF; query(1, left, right); printf("%d\n", Min); }else{ scanf("%d %d", &pos, &num); q[fa[pos]].mm=num; update(fa[pos]); } } return 0; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号