影越之线段树篇
线段树
0. 前言
- 这里是越影的笔记典藏之线段树!—— \(ysl\)_\(wf\)
忠告
-
如君是线段树初学者,本篇的入门效果极佳!?!
-
如君是线段树复习者,本篇板子的码风效果与注释效果极佳?!?
1. 引入
- 线段树是算法竞赛中常用的用来维护区间信息的数据结构。
线段树可以在 \(O(\log N)\) 的时间复杂度内实现单点修改、区间修改、区间查询(区间求和、求区间最值)等操作。
2. 线段树的基本结构与建立
2.1 分析
-
注意:如若君是复习者,本章详细介绍了标记不下放(永久化)的写法,愿君有收获!
-
线段树的建树本质是对区间的二分,而叶子结点便是单点(也就是我们所访问的初始信息)!而剩下的父节点以及根节点便是我们题目中做要求的区间和或者区间最值!(如图)
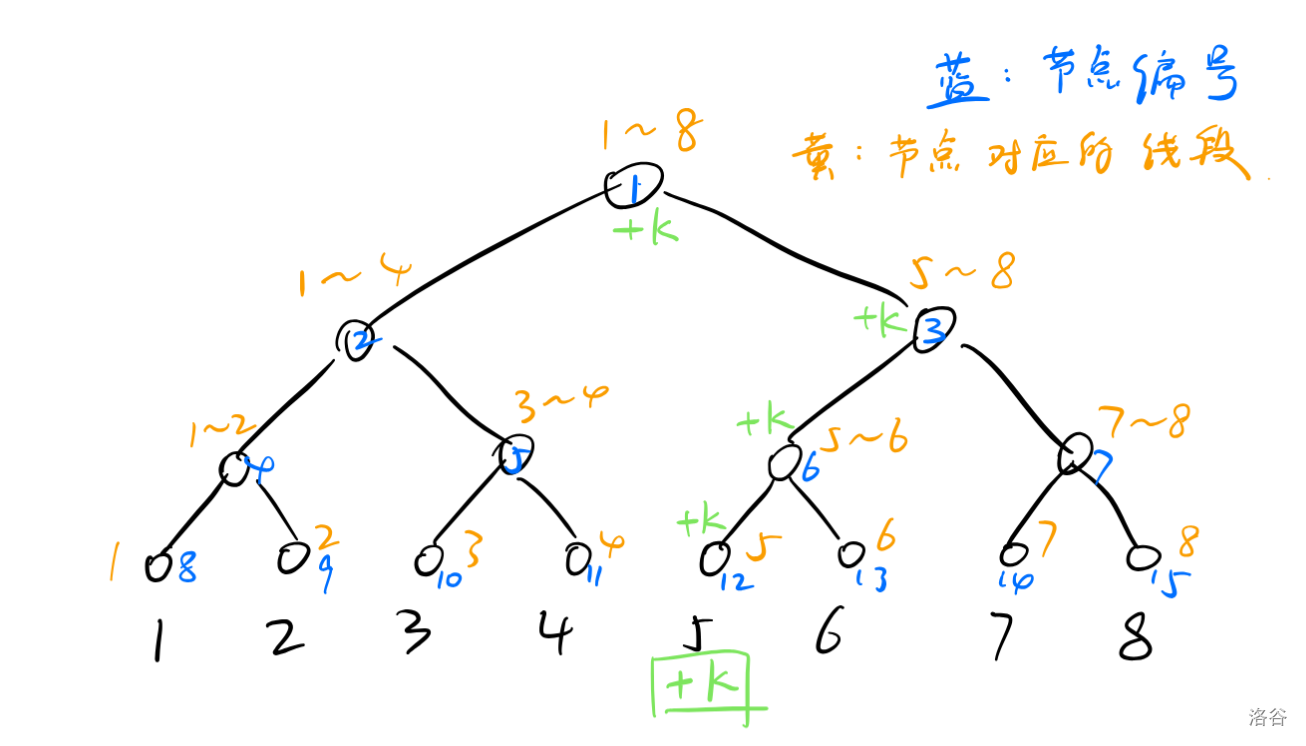
这里,我们令 \(sum_i\) 表示 \(i\) 号节点对应的线段上所有数之和。
例如:
给 \(x\) 号位置加上 \(k\)。
- 例如:\(x = 5\)(给 \(4\) 个点 \(+k\))(如图绿色,二分显然操作一次是 \(O(\log N)\))
询问 \(3\)~\(8\) 中所有数之和?
输出 \(sum_3 + sum_5\) 即可。
- 通过观察,蓝色的节点编号,我们便可以得到如下结论:
\(u\):\([l, r]\);\(mid = (l+r) / 2\)。
\(u\) 的左儿子:\([l, mid]\),编号:\(u<<1\)。
\(u\) 的右儿子:\([mid+1, r]\),编号:\(u<<1|1\)。这里,我们规定:\(N = 10^5\),则 \(sum[N*4]\)。
2.2 Code 实现
2.2.1 建树
- 详细内容皆在注释中,君定能看懂!
typedef long long lt;
const lt N = 1e4 + 10;
lt a[N], dx[N*4];
void build(lt l, lt r, lt p){
// 对 [l, r] 区间建立线段树,当前根的编号为 p
if(l == r){
dx[p] = a[l];
return ;
}
lt mid = l + ((r - l) >> 1);
// 移位运算符的优先级小于加减法,所以加上括号
// 如果写成 (l + r) >> 1,可能会超出 int 范围
build(l, mid, p<<1), build(mid + 1, r, p<<1|1);
// 递归对左右区间建树
dx[p] = dx[p<<1] + dx[p<<1|1];
}
2.2.2 直接 add 加
typedef long long lt;
const lt N = 500005;
lt sum[N*4], n;
// u: 当前节点编号
// [l,r]: 当前节点所表示的线段
// x: 要 +k 的位置
void add(lt u, lt l, lt r, lt x, lt k){
if(l==r){
sum[u] += k;
return;
}
lt mid = (l+r) / 2;
if(x <= mid) add(u<<1, l, mid, x, k);
else add(u<<1|1, mid+1, r, x, k);
sum[u] = sum[u<<1] + sum[u<<1|1];
}
int main(){
// 如果我现在有“让位置5加上9”的需求,应该:
add(1, 1, n, 5, 9);
}
3. 线段树的区间查询
这里我们以区间和为例进行讲解。
通过上述基本结构中的例子,一个区间和在线段树可能就是一个节点表示的区间,也可能是多个节点表示的区间的和!
我们依然使用二分进入左儿子和右儿子的思路!
我想,注释应该相当清晰
// get_sum(u,l,r,x,y)
// 求的是 [l,r] 和 [x,y] 交集的和
// u: 当前节点编号
// [l,r]: 当前节点所表示的线段
// [x,y]: 求和区间
lt get_sum(lt u, lt l, lt r, lt x, lt y){
// 如果当前节点完全落在求和区间内,直接返回sum
if(x<=l && r<=y) return sum[u];
lt mid = (l+r) / 2;
lt res = 0;
// 否则,说明当前节点不完全落在求和区间内,需要递归
// 我们把 [l,r] 与 [x,y] 的交集 拆分成 “[l,mid] 与 [x,y] 的交集” + “[mid+1,r] 与 [x,y] 的交集”
if(x <= mid) //这说明求和区间和左儿子表示的区间有交集
res += get_sum(u<<1, l, mid, x, y);
if(y > mid) //这说明求和区间和右儿子表示的区间有交集
res += get_sum(u<<1|1, mid+1, r, x, y);
return res;
}
也可以这样(没区别)(个人书写线段树的两种形式):
typedef long long lt;
const lt N = 1e4 + 10;
lt a[N], dx[N*4];
lt get_sum(lt l, lt r, lt x, lt y, lt p){
// [l, r] 为查询区间(询问区间),[x, y]为当前节点包含的区间(线段树二分区间),p 为当前节点的编号
if(l <= x && y <= r){
return dx[p];
}
lt mid = x + ((y - x) >> 1), sum = 0;
if(l <= mid) sum += get_sum(l, r, x, mid, p<<1);
// 如果左儿子代表的区间 [x, mid] 与询问区间有交集, 则递归查询左儿子
if(r > mid) sum += get_sum(l, r, mid + 1, y, p<<1|1);
// 如果右儿子代表的区间 [mid + 1, y] 与询问区间有交集, 则递归查询右儿子
return sum;
}
4. 懒惰标记(Pushdown法)
- 这是线段树的优化核心!以后的每一道有关线段树的题都有它的身影!
4.1 原理
如果要求修改区间 \([l, r]\),把所有包含该区间的节点都遍历一遍、修改一次,时间复杂度是无法承受的!因此,我们这里引入一个叫 「懒惰标记」 的东西。
懒惰标记,简单来说,就是通过延迟对节点信息的更改,从而减少可能不必要的操作次数。每次执行修改时,我们通过打标记的方法表明该节点对应的区间在某一次操作中被更改,但不更新该节点的子节点的信息。实质性的修改则在下一次访问带有标记的节点时才进行。
这样子,就可以做到对节点信息的延迟更改,并且,也不会造成任何答案上的影响!
4.2 push up
顾名思义,就是合并左右儿子的信息操作(以 \(+\) 为例)
void push_up(lt p){
dx[p] = dx[p<<1] + dx[p<<1|1];
}
4.3 push down
- 懒标记下传左右儿子
void push_down(lt p, lt x, lt y){
lt mid = x + ((y - x) >> 1);
if(lazy[p]){
// 如果当前节点的懒标记非空,则更新当前节点两个子节点的值和懒标记值
dx[p<<1] += lazy[p] * (mid - x + 1);
dx[p<<1|1] += lazy[p] * (y - mid);
lazy[p<<1] += lazy[p], lazy[p<<1|1] += lazy[p]; // 将标记下传给子节点
lazy[p] = 0;// 清空当前节点的标记
}
}
接下来,就是板子时间!
4.4 区间加上某个值
注释是绝对可食用的!
typedef long long lt;
const lt N = 1e4 + 10;
lt a[N], dx[N*4], lazy[N*4];
void push_up(lt p){
dx[p] = dx[p<<1] + dx[p<<1|1];
}
void push_down(lt p, lt x, lt y){
lt mid = x + ((y - x) >> 1);
if(lazy[p]){
// 如果当前节点的懒标记非空,则更新当前节点两个子节点的值和懒标记值
dx[p<<1] += lazy[p] * (mid - x + 1);
dx[p<<1|1] += lazy[p] * (y - mid);
lazy[p<<1] += lazy[p], lazy[p<<1|1] += lazy[p]; // 将标记下传给子节点
lazy[p] = 0;// 清空当前节点的标记
}
}
void update(lt l, lt r, lt s, lt x, lt y, lt p){
// [l, r] 为修改区间(询问区间), s 为被修改的元素的变化量, [x, y] 为当前节点包含的区间(线段树二分区间), p 为当前节点的编号
if(l <= x && y <= r){
dx[p] += (y-x+1) * s, lazy[p] += s;
return ;
}// 当前区间为修改区间的子集时直接修改当前节点的值,然后打标记,结束修改
lt mid = x + ((y - x) >> 1);
push_down(p, x, y);
if (l <= mid) update(l, r, s, x, mid, p<<1);
if (r > mid) update(l, r, s, mid + 1, y, p<<1|1);
push_up(p);
}
4.5 区间查询(区间求和)
- 注意:查询时也要记得懒标记下传!因为懒标记永远存在!并且在询问左右儿子前!
typedef long long lt;
const lt N = 1e4 + 10;
lt a[N], dx[N*4], lazy[N*4];
void push_down(lt p, lt x, lt y){
lt mid = x + ((y - x) >> 1);
if(lazy[p]){
// 如果当前节点的懒标记非空,则更新当前节点两个子节点的值和懒标记值
dx[p * 2] += lazy[p] * (mid - x + 1);
dx[p * 2 + 1] += lazy[p] * (y - mid);
lazy[p * 2] += lazy[p], lazy[p * 2 + 1] += lazy[p];// 将标记下传给子节点
lazy[p] = 0;// 清空当前节点的标记
}
}
lt get_sum(lt l, lt r, lt x, lt y, lt p){
// [l, r] 为查询区间, [x, y] 为当前节点包含的区间(线段树二分区间), p 为当前节点的编号
if (l <= x && y <= r) return dx[p];
// 当前区间为询问区间的子集时直接返回当前区间的和
lt mid = x + ((y - x) >> 1);
push_down(p, x, y);
lt sum = 0;
if (l <= mid) sum += get_sum(l, r, x, mid, p * 2);
if (r > mid) sum += get_sum(l, r, mid + 1, y, p * 2 + 1);
return sum;
}
4.6 区间修改
- 如果你是要实现区间修改为某一个值而不是加上某一个值的话
typedef long long lt;
const lt N = 1e4 + 10;
lt a[N], dx[N*4], lazy[N*4];
lt vis[N*4];// 额外数组储存 是否 修改值
void push_up(lt p){
dx[p] = dx[p * 2] + dx[p * 2 + 1];
}
void push_down(lt p, lt x, lt y){
lt mid = x + ((y - x) >> 1);
if(vis[p]){
dx[p * 2] = lazy[p] * (mid - x + 1);
dx[p * 2 + 1] = lazy[p] * (y - mid);
lazy[p * 2] = lazy[p * 2 + 1] = lazy[p];
vis[p * 2] = vis[p * 2 + 1] = 1;
vis[p] = 0;
}
}
void update(lt l, lt r, lt s, lt x, lt y, lt p){
// [l, r] 为修改区间, s 为被修改的元素的变化量, [x, y] 为当前节点包含的区间(线段树二分区间), p 为当前节点的编号
if(l <= x && y <= r){
dx[p] = (y-x+1) * s, lazy[p] = s;
vis[p] = 1;
return ;
}
lt mid = x + ((y - x) >> 1);
push_down(p, x, y);
if (l <= mid) update(l, r, s, x, mid, p * 2);
if (r > mid) update(l, r, s, mid + 1, y, p * 2 + 1);
push_up(p);
}
lt get_sum(lt l, lt r, lt x, lt y, lt p){
if (l <= x && y <= r) return dx[p];
lt mid = x + ((y - x) >> 1);
push_down(p, x, y);
lt sum = 0;
if (l <= mid) sum += get_sum(l, r, x, mid, p * 2);
if (r > mid) sum += get_sum(l, r, mid + 1, y, p * 2 + 1);
return sum;
}
4.7 最后:区间加、区间乘、区间求和
- 我有一版现成的 区间加、区间乘、区间求和 三合一的代码(板子2)
这个就相当要注意细节!因为要我们需要两个标记,一个是 \(lazy_{add}\)、\(lazy_{mult}\)
// 区间加、区间乘、区间求和
#include <bits/stdc++.h>
using namespace std;
typedef long long lt;
const int N = 500005;
lt n, m, Mod, a[N];
lt sum[N*4], lazy_add[N*4], lazy_mult[N*4];
// lazy_add[u]=k, lazy_mult[u]=p 表示:[l,r]整个区间的每个数都应该先*p再+k(注意:此时sum[u]是已经更新过了)
// push_up 的作用是更新sum[u]
void push_up(lt u){
sum[u] = (sum[u<<1] + sum[u<<1|1]) % Mod;
}
// push_down 的作用是 把u的lazy标记清空,并且传递给左右儿子
void push_down(lt u, lt l, lt r){
(lazy_mult[u<<1] *= lazy_mult[u]) %= Mod;
(lazy_mult[u<<1|1] *= lazy_mult[u]) %= Mod;
// 左儿子本应该 *p1 + k1
// 现在,u的lazy标记要求整个区间 *p
// (左儿子就应该 *p1 + k1) * p,所以左儿子的 lazy_add 也要 *p
(lazy_add[u<<1] *= lazy_mult[u]) %= Mod;
(lazy_add[u<<1|1] *= lazy_mult[u]) %= Mod;
(sum[u<<1] *= lazy_mult[u]) %= Mod;
(sum[u<<1|1] *= lazy_mult[u]) %= Mod;
lazy_mult[u] = 1;
(lazy_add[u<<1] += lazy_add[u]) %= Mod;
(lazy_add[u<<1|1] += lazy_add[u]) %= Mod;
lt mid = (l+r) / 2;
(sum[u<<1] += lazy_add[u] * (mid-l+1)) %= Mod;
(sum[u<<1|1] += lazy_add[u] * (r-mid)) %= Mod;
lazy_add[u] = 0;
}
// 建立初始线段树,一次 build(1,1,n) 的复杂度是 O(n)
// T(n) = 2*T(n/2) + O(1) = O(n)
// 不要和这个混淆: T(n) = 2*T(n/2) + O(n) = O(n log n)
void build(lt u, lt l, lt r){
lazy_add[u] = 0;
lazy_mult[u] = 1;
if(l==r){
sum[u] = a[l];
return;
}
lt mid = (l+r) / 2;
build(u<<1, l, mid);
build(u<<1|1, mid+1, r);
push_up(u);
}
void multi(lt u, lt l, lt r, lt x, lt y, lt k){
if(x==l && r==y){
(sum[u] *= k) %= Mod;
(lazy_mult[u] *= k) %= Mod;
(lazy_add[u] *= k) %= Mod;
return;
}
int mid = (l+r) / 2;
push_down(u, l, r);
// 分三种情况
if(y <= mid) // [x,y] 全在左儿子里
multi(u<<1, l, mid, x, y, k);
else if(x > mid) // [x,y] 全在右儿子里
multi(u<<1|1, mid+1, r, x, y, k);
else{ // [x,y] 一部分在左儿子里、一部分在右儿子里
multi(u<<1, l, mid, x, mid, k);
multi(u<<1|1, mid+1, r, mid+1, y, k);
}
push_up(u);
}
// add(u,l,r,x,y,k)
// 做的是:把 [l,r] 和 [x,y] 交集的地方 +k
// u: 当前节点编号
// [l,r]: 当前节点所表示的线段
// [x,y]: 要 +k 的位置
void add(lt u, lt l, lt r, lt x, lt y, lt k){
if(x==l && r==y){
(sum[u] += k * (r-l+1)) %= Mod;
(lazy_add[u] += k) %= Mod;
return;
}
lt mid = (l+r) / 2;
push_down(u, l, r);
// 分三种情况
if(y <= mid) // [x,y] 全在左儿子里
add(u<<1, l, mid, x, y, k);
else if(x > mid) // [x,y] 全在右儿子里
add(u<<1|1, mid+1, r, x, y, k);
else{ // [x,y] 一部分在左儿子里、一部分在右儿子里
add(u<<1, l, mid, x, mid, k);
add(u<<1|1, mid+1, r, mid+1, y, k);
}
push_up(u);
}
// get_sum(u,l,r,x,y)
// 求的是 [l,r] 和 [x,y] 交集的和
// u: 当前节点编号
// [l,r]: 当前节点所表示的线段
// [x,y]: 求和区间
lt get_sum(lt u, lt l, lt r, lt x, lt y){
// 如果当前节点完全落在求和区间内,直接返回sum
if(x<=l && r<=y) return sum[u];
// 在递归访问左右儿子之前,必须push down以保证左右儿子的sum是最新的
push_down(u, l, r);
int mid = (l+r) / 2;
// 分三种情况
lt res = 0;
if(y <= mid) // [x,y] 全在左儿子里
res += get_sum(u<<1, l, mid, x, y);
else if(x > mid) // [x,y] 全在右儿子里
res += get_sum(u<<1|1, mid+1, r, x, y);
else{ // [x,y] 一部分在左儿子里、一部分在右儿子里
res += get_sum(u<<1, l, mid, x, mid);
res += get_sum(u<<1|1, mid+1, r, mid+1, y);
}
push_up(u);
return res % Mod;
}
int main(){
int n, m, op, x, y;
lt k;
scanf("%d%d%d", &n, &m, &Mod);
for(int i = 1; i <= n; i++)
scanf("%d", a + i); // a+i 等价于 &a[i]
build(1, 1, n);
while(m--){
scanf("%d%d%d", &op, &x, &y);
if(op==1) scanf("%lld", &k), multi(1,1,n,x,y,k);
else if(op==2) scanf("%lld", &k), add(1,1,n,x,y,k);
else printf("%lld\n", get_sum(1,1,n,x,y));
}
return 0;
}
5. 技巧:标记永久化
这个东西有一个优点,不需要 \(push\) \(down\),所以在一定程度上,降低了时间常数,也在一定程度上降低了代码的复杂度!
问:标记不下传,你这玩意在区间求和时懒标记的内容没有记录在案啊!!!
答:说得好!那我们为什么不能让他记录在案呢?
lt res = lazy[u] * (y-x+1);//在 get_sum 的一开始!
这时,线段树1的代码也就有了永久化版本!(相当好理解!)
// 区间加、区间求和
#include <bits/stdc++.h>
using namespace std;
typedef long long lt;
const lt N = 500005;
lt n, m;
lt sum[N*4], lazy[N*4];
// lazy[u]=k 表示:[l,r]整个区间都应该 +k,但是这整个区间的 sum 都没有加
// add(u,l,r,x,y,k)
// 做的是:把 [l,r] 和 [x,y] 交集的地方 +k
// u: 当前节点编号
// [l,r]: 当前节点所表示的线段
// [x,y]: 要 +k 的位置
void add(lt u, lt l, lt r, lt x, lt y, lt k){
if(x==l && r==y){
lazy[u] += k;
return;
}
sum[u] += k * (y-x+1);
lt mid = (l+r) / 2;
// 分三种情况
if(y <= mid) // [x,y] 全在左儿子里
add(u<<1, l, mid, x, y, k);
else if(x > mid) // [x,y] 全在右儿子里
add(u<<1|1, mid+1, r, x, y, k);
else{ // [x,y] 一部分在左儿子里、一部分在右儿子里
add(u<<1, l, mid, x, mid, k);
add(u<<1|1, mid+1, r, mid+1, y, k);
}
}
// get_sum(u,l,r,x,y)
// 求的是 [l,r] 和 [x,y] 交集的和
// u: 当前节点编号
// [l,r]: 当前节点所表示的线段
// [x,y]: 求和区间
lt get_sum(lt u, lt l, lt r, lt x, lt y){
// 如果当前节点完全落在求和区间内,直接返回sum
lt res = lazy[u] * (y-x+1);
if(x<=l && r<=y) return sum[u] + res;
lt mid = (l+r) / 2;
// 分三种情况
if(y <= mid) // [x,y] 全在左儿子里
res += get_sum(u<<1, l, mid, x, y);
else if(x > mid) // [x,y] 全在右儿子里
res += get_sum(u<<1|1, mid+1, r, x, y);
else{ // [x,y] 一部分在左儿子里、一部分在右儿子里
res += get_sum(u<<1, l, mid, x, mid);
res += get_sum(u<<1|1, mid+1, r, mid+1, y);
}
return res;
}
int main(){
int n, m, op, x, y;
lt k;
scanf("%d%d", &n, &m);
for(int i = 1; i <= n; i++){
scanf("%d", &x);
add(1, 1, n, i, i, x);
}
while(m--){
scanf("%d%d%d", &op, &x, &y);
if(op==1) scanf("%lld", &k), add(1,1,n,x,y,k);
else printf("%lld\n", get_sum(1,1,n,x,y));
}
return 0;
}
5.1 弊端
他不可以用在区间修改的题目中(呜呜呜)
但是!他却也可以用在区间最值中!!!
具体这道题:[NOI2016] 区间
部分代码展示:
void add(lt now, lt l, lt r, lt x, lt y, lt z){//区间加和区间max也可以用永久化
if(l == x && r == y){
lazy[now] += z; sum[now] += z;
return ;
}
lt mid = l+r>>1;
if(x <= mid) add(now<<1, l, mid, x, min(mid, y), z);
if(y > mid) add(now<<1|1, mid+1, r, max(x, mid+1), y, z);
sum[now] = max(sum[now<<1], sum[now<<1|1]) + lazy[now];
}
结论:一般出现在区间加、区间求和、区间最值等题目!
6. 区间最值操作 & 区间历史最值
7. 动态开点线段树
8. 扫描线
9. 李超线段树
10. 线段树优化建图
首先我们可以有一种直觉,在我上面的图中,也可以看出,线段树虽说是一种数据结构,但是,它看起来还是像一棵树!这就启示我们它可以用来优化建图
在建图连边的过程中,我们有时会碰到这种题目,一个点向一段连续的区间中的点连边或者一个连续的区间向一个点连边,如果我们真的一条一条连过去,那一旦点的数量多了复杂度就爆炸了,这里就需要用线段树的区间性质来优化我们的建图了。
从 板子啊(Legacy) 入手。
显然,如果暴力建边,一定会爆炸!
这时候,就需要运用线段树的区间化点连边的思想(名字自己起的)!
思路:用两颗线段树,一颗只连自上而下的边,一颗只连自下而上得边,询问的内容就是在两颗线段树间连边!
坑点:两颗线段树的叶子结点对应的其实是同一个点,因此他们互相之间连边权为 \(0\) 的边。
Code 如下(有注释):
#include<bits/stdc++.h>
using namespace std;
typedef long long lt;
const lt N = 3e6 + 5, K = 5e5, inf = 0x3f3f3f3f3f3f3f3fll;
lt n, m, s, opt, x, y, z, l, r, w, a[N];
lt cnt, hd[N], to[N], nxt[N], val[N], d[N];
bool v[N];
priority_queue<pair<lt, lt>> q;
void re_and_wr(){
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
}
void add(lt x, lt y, lt z){
to[++cnt] = y, nxt[cnt] = hd[x], hd[x] = cnt, val[cnt] = z;
}
void build(lt p, lt l, lt r){
if(l == r){//a: 记录叶子节点的编号
a[l] = p;
return ;
}
lt mid = (l+r)/2;
add(p, p<<1, 0), add(p, p<<1|1, 0);//出树(从 p 向 p 的左右儿子连一条边权为 0 的边)
add((p<<1)+K, p+K, 0), add((p<<1|1)+K, p+K, 0);//入树(从 p 的左右儿子向 p 连一条边权为 0 的边)
build(p<<1, l, mid);
build(p<<1|1, mid+1, r);
}
void modify(lt p, lt l, lt r, lt x, lt y, lt v, lt w){
if(l >= x && r <= y){//如果当前区间被涵盖
if(opt == 2) add(v+K, p, w);//对于操作二,就从入树的叶子节点向出树中的对应区间连边。
else add(p+K, v, w);//对于操作三,就从入树中的对应区间向出树中的叶子节点连边。
return ;
}
lt mid = (l+r)/2;
if(x <= mid) modify(p<<1, l, mid, x, y, v, w);
if(y > mid) modify(p<<1|1, mid+1, r, x, y, v, w);
}
void Dijkstra(lt s){
memset(d, 0x3f, sizeof d), d[s] = 0;
q.push(make_pair(0, s));
while(q.size()){
lt x = q.top().second; q.pop();
if(v[x]) continue;
v[x] = 1;
for(lt i = hd[x]; i; i = nxt[i]){
lt y = to[i], z = val[i];
if(d[y] > d[x] + z) d[y] = d[x] + z, q.push(make_pair(-d[y], y));
}
}
}
int main(){
// freopen("6.in", "r", stdin);
// freopen("6.out", "w", stdout);
re_and_wr();
cin >> n >> m >> s; build(1, 1, n);
for(int i = 1; i <= n; i++){
add(a[i], a[i]+K, 0), add(a[i]+K, a[i], 0); //两棵线段树的叶子节点之间连边
}
for(int i = 1; i <= m; i++){
cin >> opt;
if(opt == 1) cin >> x >> y >> z, add(a[x]+K, a[y], z);//对于操作一,就从入树的叶子节点向出树的叶子节点连边。
else{
cin >> x >> l >> r >> w;
modify(1, 1, n, l, r, a[x], w);
}
}
Dijkstra(a[s]+K);
for(int i = 1; i <= n; i++){
lt ans = d[a[i]] != inf ? d[a[i]] : -1;
cout << ans << ' ';
}
return 0;
}
11. 线段树合并
12. 线段树分裂
13. 线段树优化 DP
后记
修改记录
- \(2024.8.14\) —— 第一次整理。
缺失部分:\(6.\)~\(12.\) - \(2024.8.15\) —— 第二次整理。
添加:\(10.\)
参考资料
- oi-wiki
肺腑
- 愿君在影越这里受益匪浅。—— \(ysl\)_\(wf\)

