影越之图论篇

图论

0. 前言

这里是影越的笔记典藏之图论！—— $ysl$_$wf$

忠告

持续精进与整理，发布并不意味着本篇的终止！
因为，图论没有极限！
如果君是初学者，助汝 OI 的学习中通俗易懂的了解、运用，若想深究本质，本篇也可作为良好的敲门砖！
如果君是复习者，本篇一定可以让你的回忆收益最大化！看完基本只剩做题的东风了！

1. 基本简介

图论（$Graph$ $theory$）是数学的一个分支，图是图论的主要研究对象。图（$Graph$）是由若干给定的顶点及连接两顶点的边所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系。顶点用于代表事物，连接两顶点的边则用于表示两个事物间具有这种关系。

具体入门请见此处。

2. 图的存储

二维数组 graph[i][j] = 1 表示 $i$ 到 $j$ 有连边，$0$ 则表示没有连边

无向图 = 双向图：graph[i][j] = graph[j][i] = 1

这里我们只介绍两种常用的（具体四种存法请见 oi-wiki）：

2.1【Method-1】vector存法

2.1.1 了解 vector 动态数组

vector<int> a; //一个存储int类型元素的动态数组，空的，啥都没有

a.push_back(2); //向 a 的最后面添加一个元素 2
a.push_back(5); //向 a 的最后面添加一个元素 5
// 注意vector内部的存储下标从0开始
// a[0]=2, a[1]=5
a[0]=7; // 把 a[0] 改成 7
// a.size() 表示 a 里面有多少个元素
for(int i = 0; i < a.size(); i++){
    cout << a[i] << " ";
}
// 注意：如果访问 a[2] 会报错（RE）！！！
a[2] = 10; // 直接报错！

vector<int> b;
b.resize(100); // 把 b 声明为一个长度为 100 的数组
// 这时候 b[0], b[1], ..., b[99] 都是可以用的

// sort的时候，和普通数组是不一样的
// 普通数组：sort(a+1, a+1+n)
sort(a.begin(), a.end());

// 类似的
reverse(a.begin(), a.end());
int l = lower_bound(a.begin(), a.end(), x) - a.begin();

2.1.2 用动态数组存储图。

事先告诉你，图的点数不超过 $10^5$ 个。

vector<int> g[100005];
// 每一个 g[i] 都是一个动态数组，g[i]里面存储的元素，就是 i 连向的点
// 加入一条 u 到 v 的边
g[u].push_back(v);

当然，如果你想包含每条边的边权，我们可以用一个 struct 数组来解决这一问题！

typedef long long lt;

struct Edge{
    lt v, w;
}g[N];

g[u].pussh_back((Edge){v,w});

这种方法在图论题目中具有广泛性，并且也较为常用！

2.2 【Method-2】链式前向星

本质上是用链表实现的邻接表，核心代码如下：

// head[u] 和 cnt 的初始值都为 -1
void add(int u, int v) {
  nxt[++cnt] = head[u];  // 当前边的后继
  head[u] = cnt;         // 起点 u 的第一条边
  to[cnt] = v;           // 当前边的终点
}

// 遍历 u 的出边
for (int i = head[u]; ~i; i = nxt[i]) {  // ~i 表示 i != -1
  int v = to[i];
}

参考代码：

#include<bits/stdc++.h>
using namespace std;

typedef long long lt;
lt n, m;
vector<bool> vis;
vector<lt> head, nxt, to;

void add(lt u, lt v) {
    nxt.push_back(head[u]);
    head[u] = to.size();
    to.push_back(v);
}

bool find_edge(lt u, lt v) {
    for(lt i = head[u]; ~i; i = nxt[i]){  // ~i 表示 i != -1
        if (to[i] == v) {
            return true;
        }
    }
    return false;
}

void dfs(lt u) {
    if(vis[u]) return;
    vis[u] = true;
    for(lt i = head[u]; ~i; i = nxt[i]) dfs(to[i]);
}

int main() {
    cin >> n >> m;

    vis.resize(n + 1, false);
    head.resize(n + 1, -1);

    for (int i = 1; i <= m; ++i) {
        lt u, v;
        cin >> u >> v;
        add(u, v);
    }

    return 0;
}

存各种图都很适合，但不能快速查询一条边是否存在，也不能方便地对一个点的出边进行排序。

优点是边是带编号的，有时会非常有用，而且如果 cnt 的初始值为奇数，存双向边时 i ^ 1 即是 i 的反边（常用于网络流）。

3. 拓扑排序

3.1 概念

有向无环图（DAG）：一种有向图，他没有环

拓扑排序：告诉你 $i$ 要在 $j$ 之前生产，求一个合理的生产流程

概念：入度、出度。

$i$ 的入度就是有多少条边连向 $i$

$i$ 的出度就是有多少条边从 $i$ 连出去

3.2 实现

我们现在关心入度。在读入边的时候就算出来

什么样的点可以成为第一个点？入度为 $0$ 的点。

先找一个入度为$0$的点，然后把它连出去的边删掉。找下一个入度为$0$的点。

// deg[i]: i的入度
// topo[k]: 拓扑排序的序列中第k个点
// L: 当前拓扑序列的长度
for(int u=1; u<=n; u++)
    if(deg[u]==0){
        topo[++L] = u;
    }
int p = 1;
while(L<n){
    for(int i=0; i < g[topo[p]].size(); i++){
        int v = g[topo[p]][i];
        deg[v] --;
        if(deg[v] == 0) topo[++L] = v;
    }
    p++;
}

3.3 求字典序最小的拓扑

直接改成优先队列即可！（小根堆）

4. 最长路

4.1 实现

dist[i]：表示从 $1$ 出发到 $i$ 的最长路径长度

struct Edge{
    int v,w;
};
vector<Edge> g[100005];

// g[u].push_back((Edge){v, w});
// g[u].emplace_back(v, w);
// 添加一条u到v，边权为w的边

// deg[i]: i的入度
// topo[k]: 拓扑排序的序列中第k个点
// L: 当前拓扑序列的长度
// dist[i]: 从1到i的最长路
int main(){
    int u, v, w;
    // 读入 ......
    for(int u=1; u<=n; u++){
        dist[u] = INT_MIN/2;
        if(deg[u]==0) topo[++L] = u;
    }
    dist[1] = 0;
    int p = 1;
    while(L<n){
        for(int i=0; i < g[topo[p]].size(); i++){
            int v = g[topo[p]][i].v;
            dist[v] = max(dist[v], dist[topo[p]] + g[topo[p]][i].w);
            deg[v] --;
            if(deg[v] == 0) topo[++L] = v;
        }
        p++;
    }
    // 输出 ......
}

4.2 习题

5. 最小生成树

这里摘取了核心部分，详细介绍请见影越论最小生成树篇！

5.1 概念

生成树：就是在一个连通图里选一些边，让他们恰好构成一棵树。

给你一个 $n$ 个点 $m$ 条边的图，每条边都有正的边权，求一个生成树，使得树上边权之和最小。

5.2 并查集（简析）

给你 $n$ 个独立的点，每个点都是一个独立的集合，你需要处理以下两种操作：

合并 $u$ 与 $v$ 所在的集合
询问 $u$ 与 $v$ 是否在同一个集合

vector<int> a[10];
{1} {2} {3} {4} {5} {6}
a[1].push_back(3);
a[3].push_back(1);
{1,3} {2} {4} {5} {6}
{1,3} {2,5} {4} {6}
a[1].push_back(2);
a[1].push_back(5);
a[2]..
a[3]..
a[5]..

fa[i]: 节点 $i$ 的父亲，如果 $i$ 是根，那么fa[i] = i

find(i): 寻找 $i$ 的祖先

int find(int u){
    if(fa[u] == u) return u;
    else{
        // 路径压缩
        fa[u] = find(fa[u]);
        return fa[u];
    }
}

//更简洁的写法
int find(int u){
    return (fa[u]==u) ? u : (fa[u]=find(fa[u]));
}

void merge(int u,int v){
    int x = find(u);
    int y = find(v);
    if(x==y) return;
    fa[x] = y;
    // 或 fa[y] = x
}

// 判断u和v是否在同一个集合
bool judge(int u, int v){
    int x = find(u);
    int y = find(v);
    return x==y;
}

5.3 最小生成树

把所有边按边权从小到大排序
贪心得从小到大选边，对于一条边$(u,v,w)$，判断$u$和$v$是否在同一棵树里，如果在，就不能选这条边。

struct Edge{
    int u, v, w;
};
Edge e[500005];

bool cmp(Edge a, Edge b){
    return a.w < b.w;
}

int main(){
    for(int i = 1; i <= m; i++){
        cin >> e[i].u >> e[i].v >> e[i].w;
    }
    int ans = 0, cnt = 0;
    sort(e+1, e+1+m, cmp);
    for(int i = 1; i <= n; i++) fa[i]=i;
    for(int i = 1; i <= m; i++){
        if(judge(e[i].u, e[i].v)) continue;
        ans += e[i].w;
        cnt++;
        merge(e[i].u, e[i].v);
        if(cnt==n-1) break;
    }
    if(cnt==n-1) cout << ans << endl;
    else cout << "orz" << endl;
    return 0;
}

证明：环切定理

5.4 最大瓶颈生成树

一条路径的瓶颈就是路径上边权最小的边。

货车运货，需要走一条路径，路径上的每条边都有限重，那么货车能运的最大重量就是这条路径的瓶颈。

$A$到$B$的最大瓶颈路径：所有$A$到$B$的路径中，瓶颈最大的那条。这条路径的瓶颈就称为$A$到$B$的“瓶颈距离”，也就是货车从$A$到$B$能运的最大重量

给你一个图，求一个生成树，它不改变任意两个点的瓶颈距离。

最大瓶颈生成树对任意的连通图都存在吗？

答案是肯定的，并且任意给一个连通图，他的最大瓶颈生成树就是最大生成树。（反证法证明）

[NOIP2013 提高组] 货车运输

6. 树上问题 < 五颗星！>

作为图论最重要的部分之一，详见影越论树篇！

7. 最短路 < 五颗星！>

作为图论最重要的部分之一，详见影越论最短路篇！

$. 图论连通性问题 < 五颗星！>

个人认为这是图论在 OI 中最重要的内容！

无向图连通性中的双连通分量和有向图可达性中的强连通分量分两章节介绍。

8. 有向图可达性中的强连通分量

研究有向图可达性时，强联通分量是最基本的结构。

本章讨论强联通分量，默认图的类型是 有向弱连通图

8.1 相关定义

强连通：对于有向图的两点 $u$，$v$，若它们相互可达，则称 $u$，$v$ 强连通，这种性质称为 强连通性。

显然，强连通与强连通可以构成一个更大的强连通，也就是说它们之间具有 传递性。

强连通图：满足任意两点强连通的有向图称为 强连通图。它等价于图上任意点可达其它所有点。
强联通分量：有向图的极大强连通子图称为 强联通分量（Strongly Connected Component，SCC）。

强连通分量在求解与有向图可达性相关的题目时很有用，因为在只关心可达性时，同一强连通分量内的所有点等价。

8.2 $Tarjan$ 法求 SCC

Tarjan 法求解 SCC 是 OI 赛制中最常用、甚至可以用足够来形容的算法！

8.2.1 相关概念

$dfs$ 序：深度优先搜索的遍历点的顺序！

$dfn_i$：$i$ 在 $dfs$ 序里是第几个。

$low_u$：表示 $u$ 及其⼦孙节点的返祖边所指向的最⼩ $dfs$ 序。

8.3.2 分析

$dfn_u = low_u$ 说明 $u$ 一定是一个强连通分量的开头。

（在遍历的一开始，每个点都是一个强联通，所以 $dfn_u = low_u$）

什么样的点在 $u$ 的强连通分量里？

$u$ 的强连通分量里面不会有u的祖先

$u$ 的强连通分量只有u和他的一些子孙
如果 $v$ 在 $u$ 的强连通分量里，那么 $low_v = dfn_u$

如果 $v$ 既是 $u$ 的子孙，又满足 $low_v = dfn_u$，那么v一定在u的强连通分量里，吗？—— 对！

8.3.3 实现

明确了这些，我们便可以在 $dfs$ 的过程中完成 Tarjan 的标记工作！

核心：

$u$ 的子节点遍历结束后，若 $dfn_u = low_u$，说明 $u$ 一定是一个强连通分量的开头。
这时，我们便让它和它的儿子并入一个新的“盒子”，而这个过程不妨用栈！

先上代码：（也是缩点模板例题的核心部分！）

#include<bits/stdc++.h>
using namespace std;

struct Edge{
    int u, v;
} e[500005];

vector<int> g[100005];
int dfn[100005], low[100005], cnt=0;
int scc[100005], sccn;
// scc[i]表示i在第几个强连通分量 (i所在的大点的编号)
stack<int> stk;
// push: 扔进去
// pop: 弹出顶上一个
// top: 问顶上那个是啥

int w[100005];
int sccw[100005];

void Tarjan(int u){
    stk.push(u);
    dfn[u] = low[u] = ++cnt;
    for(int v : g[u]){
        if(dfn[v]){//非树边
            if(scc[v] == 0) low[u] = min(low[u], dfn[v]);
            continue;
        }
        Tarjan(v);
        low[u] = min(low[u], low[v]);//返祖~
    }
    // dfn[u]=low[u] 表示 u 这个点是强连通分量的第一个点
    // 如何标注强连通分量里的所有点？
    if(dfn[u] == low[u]){
        sccn++;
        while( 1 ){
            if(stk.top() == u){
                scc[stk.top()] = sccn;
                stk.pop();
                break;
            }
            scc[stk.top()] = sccn;
            //cout<<sccn<<endl;
            stk.pop();
        }
    }
}


int main(){
    int u, v, m, n;
    // 读取了w

    for(int i = 1; i <= m; i++){
        cin >> u >> v;
        g[u].push_back(v);
        e[i]=(Edge){u,v};
    }

    for(int i = 1; i <= n; i++)
        if(dfn[i]==0) Tarjan(i);
    // 缩点完成之后，图里只有1,2,...,sccn这么些大点
    // 每个大点的权值是它所包含的小点权值之和

    for(int i = 1; i <= n; i++){
        sccw[scc[i]] += w[i];
        g[i].clear();
    }
    for(int i = 1; i <= m; i++){
        // 你知道小点之间的连边 e[i].u -> e[i].v
        // 对应于大点之间的连边 scc[e[i].u] -> scc[e[i].v]
        if(scc[e[i].u] == scc[e[i].v]) continue;
        g[scc[e[i].u]].push_back(scc[e[i].v]);
    }

    // 拓扑

    return 0;
}

在这其中，有一个地方比较容易出错！

if(dfn[v]){
    if(scc[v] == 0) low[u] = min(low[u], dfn[v]);
    continue;
}

为什么要加 if(scc[v] == 0)？

在这个图中，红边不是返祖边，所以 $low[3]$ 不要对 $dfn[4]$ 取 $min$。

如果一条非树边不是返祖边，那么指向的点 $v$ 肯定已被弹出，换言之，$scc[v]$ 肯定已经被附过值！

而返祖边指向的 $v$，$scc[v]$ 肯定还没赋值！

所以加 if(scc[v] == 0) 避免了上述问题！

如此，Tarjan 法秒了！

8.3 $Kosaraju$ 法求 SCC

该算法依靠两次简单的 DFS 实现：

第一次 DFS，选取任意顶点作为起点，遍历所有未访问过的顶点，并在回溯之前给顶点编号，也就是后序遍历。

第二次 DFS，对于反向后的图，以标号最大的顶点作为起点开始 DFS。这样遍历到的顶点集合就是一个强连通分量。对于所有未访问过的结点，选取标号最大的，重复上述过程。

两次 DFS 结束后，强连通分量就找出来了，Kosaraju 算法的时间复杂度为 $O(n+m)$。

8.4 $Garbow$ 法求 SCC

Garbow 算法是 Tarjan 算法的另一种实现，Tarjan 算法是用 $dfn$ 和 $low$ 来计算强连通分量的根，Garbow 维护一个节点栈，并用第二个栈来确定何时从第一个栈中弹出属于同一个强连通分量的节点。从节点 $w$ 开始的 DFS 过程中，当一条路径显示这组节点都属于同一个强连通分量时，只要栈顶节点的访问时间大于根节点 $w$ 的访问时间，就从第二个栈中弹出这个节点，那么最后只留下根节点 $w$。在这个过程中每一个被弹出的节点都属于同一个强连通分量。

当回溯到某一个节点 $w$ 时，如果这个节点在第二个栈的顶部，就说明这个节点是强连通分量的起始节点，在这个节点之后搜索到的那些节点都属于同一个强连通分量，于是从第一个栈中弹出那些节点，构成强连通分量。

9. 无向图连通性中的双连通分量

9.1 相关定义

无向图连通性，主要研究的是割点和割边

割点：在无向图中，删去后使得连通分量数增加的点称为割点。
割边：在无向图中，删去后使得连通分量数增加的边称为割边，也称桥。

注意：孤立点和孤立边的两个端点都不是割点，但孤立边是割边。非连通图的割边为其每个连通分量的并。

重要性：对于无向连通图上的非割点，删去它，图仍然连通，但删去割点后图就不连通了。因此割点相较于非割点对连通性有更大的影响。割边同理。

点双连通图：不存在割点的无向连通图称之为点双连通图。根据割点的定义，孤立点和孤立边均为点双连通图。
边双连通图：不存在割边的无向连通图称为边双连通图。根据割边的定义，孤立点是边双连通图，但孤立边不是。
点双连通分量：一张图的极大点双连通子图称为点双连通分量（V-BCC），简称点双。
边双连通分量：一张图的极大边双连通子图称为边双连通分量（E-BCC），简称边双。

9.2 双连通的基本性质

研究双连通的性质时，最重要的是把定义中的基本元素 —— 割点和割边的性质理清楚。然后从整体入手，考察对应分量在原图上的分布形态，再深入单个分量，考察分量内两点之间的性质。以求对该连通性以及连通分量有直观的印象，思考时有清晰的图像作为辅助，做题思路更流畅。

9.2.1 边双连通

9.2.1 点双连通

9.3 求割点（割顶）

对于树边 $(u, v)$，如果 $low_v \ge dfn_u$，即 $v$ 和其子树能够通过返祖边回溯到时间戳最小只能 $dfn_u$，那么要把它们的时间戳回溯到 $dfn_u$ 之前就需要与 $u$ 相关的边。也就是说这时如果 $u$ 去掉，与其有关的边全部消失，那么 $low_v$ 不可能小于等于 $dfn_u$，也就是不可能回溯到时间戳比 $u$ 更小的点，此时这个子树与其它点无法连通，$u$ 就是割点。

注意：一个连通分量的搜索树的根节点一定满足上面的条件，因为在这个搜索树中，不存在一个 $dfn$ 值比它小的节点，但是当且仅当其至少拥有两个以上的子树，它才能被称为割点。

坑点：如果这个图只存在根节点和其中一个子树时，由于根节点是第一访问的节点，它会被我们上面的判断条件误判为割点，但是它并不是一个割点，而当它有多个子树时，删除它会使得子树不再连通，这时它才是一个割点。

所以，割点，无非是在 Tarjan 代码的基础上了一句话：if(low[v] >= dfn[u]) cut[u] = true;

核心代码：

void Tarjan(int u, int fa){
	int son = 0;//子树个数
	low[u] = dfn[u] = ++cnt;//打上时间戳标记
	stk.push(u);//u进入搜索树
	for(int v : g[u]){
		if(!dfn[v]){//树边
			son++;
			Tarjan(v, u);
			low[u] = min(low[u], low[v]);
			if(low[v] >= dfn[u]) cut[u] = true;
		}
		else if(v != fa) low[u] = min(low[u], dfn[v]);//返祖边
	}
	if(fa == 0 && son < 2) cut[u] = false;//是根节点，且子树小于2，不是割点
}

int main{
    for(int i = 1; i <= n; i++){
		if(dfn[i] == 0){
			//stk.clear();只能手动清空
			while(!stk.empty()){
				stk.pop();
			} 
			Tarjan(i, 0);
		}
	} 
}

9.4 求点双连通分量

9.4.1 分析

两个点双最多只有一个公共点（即都有边与之相连的点）；且这个点在这两个点双和它形成的子图中是割点。

对于第一点，因为当它们有两个及以上公共点时，它们可以合并为一个新的点双（矩形代表一个点双，圆形代表公共点）：

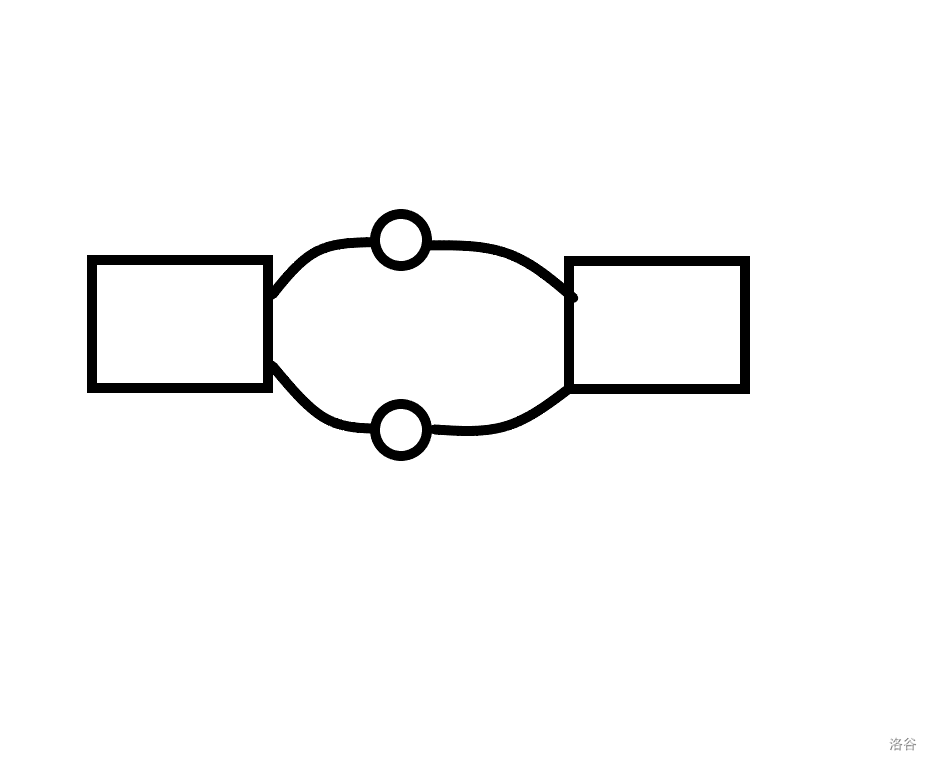
当有两个及以上公共点时，删除其中一个点及其与两个点双相连的边后，这两个点双总是可以通过另一个公共点到达彼此，属于一个连通分量，所以这些公共点对于这个子图而言并不是一个割点，按照定义，这两个点双和这些公共点应该是一个更大的点双。

对于第二点，与第一点类似，当对于这个子图而言它不是一个割点时，这两个点双也可以合并为一个新的点双：

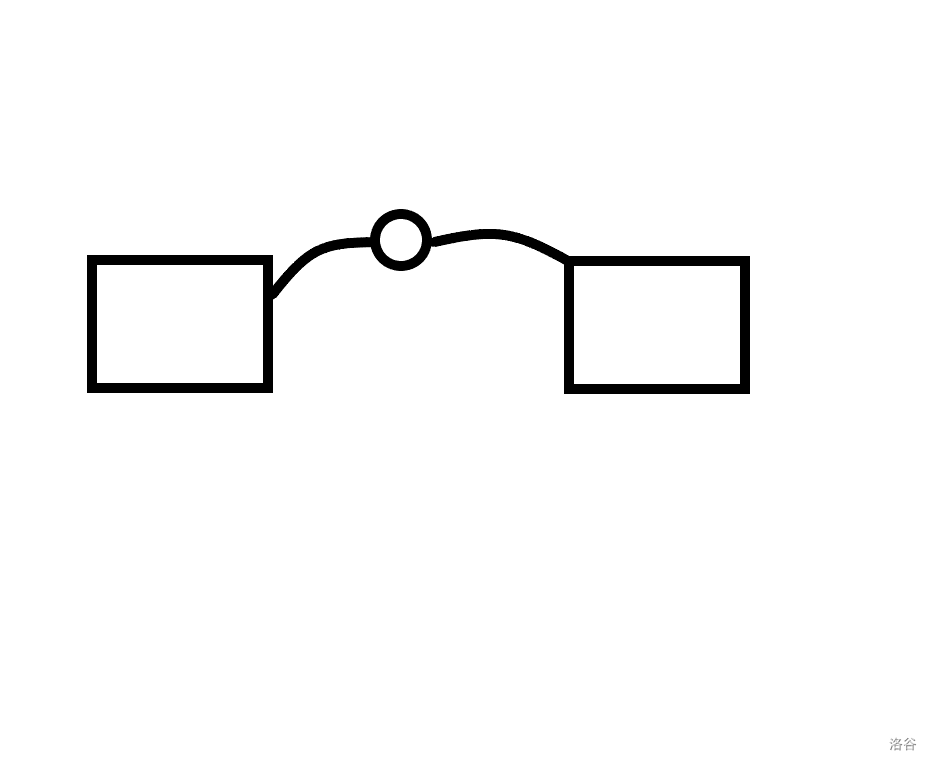
9.4.2 实现核心

当这个公共点对于这个子图不是一个割点时，也就意味着这两个点双有着另外的边相连，而这些边相连的点同样也是两个点双的公共点，可以归到第一种情况里。

对于一个点双，它在 DFS 搜索树中 $dfn$ 值最小的点一定是割点或者树根。

当这个点是割点时，它所属的点双必定不可以向它的父亲方向包括更多点，因为一旦回溯，它就成为了新的子图的一个割点，不是点双。所以它应该归到其中一个或多个子树里的点双中。

当这个点是树根时，它的 $dfn$ 值是整棵树里最小的。它若有两个以上子树，那么它是一个割点；它若只有一个子树，它一定属于它的直系儿子的点双，因为包括它；它若是一个独立点，视作一个单独的点双。

换句话说，一个点双一定在这两类点的子树中。

我们用栈维护点，当遇到这两类点时，将子树内目前不属于其它点双的非割点或在子树中的割点归到一个新的点双。注意这个点可能还是与其它点双的公共点，所以不能将其出栈。

板题代码如下：

#include<bits/stdc++.h>
using namespace std;

typedef long long lt;
const int N = 2e6 + 10;
struct Edge{
	int u, v;
}e[N];
vector<int> g[N];
int dfn[N], low[N], cnt = 0;
int scc[N], sccn;
stack<int> stk;
bool cut[N];

lt bcc;
vector<lt> ans[N];

void Tarjan(int u, int fa){
	int son = 0;
	low[u] = dfn[u] = ++cnt;
	stk.push(u);
	for(int v : g[u]){
		if(!dfn[v]){
			son++;
			Tarjan(v, u);
			low[u] = min(low[u], low[v]);
			if(low[v] >= dfn[u]){
				bcc++;
                cut[u] = true;
                while(stk.top() != v){
                    ans[bcc].push_back(stk.top()); 
                    stk.pop();//将子树出栈
                }
				ans[bcc].push_back(stk.top()); stk.pop();
                ans[bcc].push_back(u);//把割点/树根也丢到点双里
            }
		}
		else if(v != fa) low[u] = min(low[u], dfn[v]);
	}
	if(fa == 0 && son < 2) cut[u] = false;
    if(fa == 0 && son == 0) ans[++bcc].push_back(u);//特判独立点
}

int main(){
	int n, m, u, v;
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= m; i++){
		scanf("%d%d", &u, &v);
		g[u].push_back(v);
		g[v].push_back(u);
		e[i] = (Edge){u, v};
	}
	for(int i = 1; i <= n; i++){
		if(dfn[i] == 0){
			//stk.clear();只能手动清空
			while(!stk.empty()){ stk.pop(); }
			Tarjan(i, 0);
		}
	}
    printf("%lld\n", bcc);
    for(lt i = 1; i <= bcc; i++){
        printf("%d ", (int)ans[i].size());
		for(int j : ans[i]) printf("%lld ", j);
		printf("\n");
    }
	return 0;
}

9.5 求割边

它的求解思路与割点几乎是一样的！

先上代码：

void Tarjan(int u, int fa){
	int son = 0;
	low[u] = dfn[u] = ++cnt;
	stk.push(u);
	for(auto p : g[u]){
        lt v = p.first;
		if(!dfn[v]){
			son++;
			Tarjan(v, p.second);
			low[u] = min(low[u], low[v]);
			if(low[v] > dfn[u]) cut[p.second] = true;//割边
		}
		else if(p.second != fa) low[u] = min(low[u], dfn[v]);
	}
}

int main{
    for(int i = 1; i <= n; i++){
		if(dfn[i] == 0){
			//stk.clear();只能手动清空
			while(!stk.empty()) stk.pop();
			Tarjan(i, 0);
		}
	}
}

它割点的区别如下：

割点：

...
if(low[v] >= dfn[u]) cut[u] = true;
...
if(fa == 0 && son < 2) cut[u] = false;//是根节点，且子树小于2，不是割点

割边：

...
if(low[v] > dfn[u]) cut[p.second] = true;//割边
...
不特判根节点！

因为不特判根节点，所以是 >！显然，割点和割边的性质是类似的，所以割边代码实现无非的细节是选边节点进行边的标记的操作！

这里，我使用了 pair。

9.6 求边双连通分量

我们顺着求出割边的思路，割边的两边不就是边双吗？那么我们只需要跑一遍 $dfs$ 进行“缩点”，而条件是割边或属于其他分量！

板题核心代码：

void dfs(lt s, lt dccn){
    dcc[s] = dccn;
    for(auto p : g[s]){
        lt v = p.first;
        if(dcc[v] || cut[p.second]) continue;
        // 如果这个点属于其他分量或者这条边是割边，就停止搜索。
        dfs(v, dccn);
    }
}

int main(){
    for(int i = 1; i <= n; i++){
		if(dfn[i] == 0){
			//stk.clear();只能手动清空
			while(!stk.empty()) stk.pop();
			Tarjan(i, 0);
		}
	} 
}

完整：

#include<bits/stdc++.h>
using namespace std;

typedef long long lt;
const int N = 2e6 + 10;
struct Edge{
	int u, v;
}e[N];
vector<pair<int,int>> g[N];
int dfn[N], low[N], cnt = 0;
stack<int> stk;

bool cut[N];//割边

lt dccn;
lt dcc[N];
vector<lt> dccs[N];

void Tarjan(int u, int fa){//割边
	int son = 0;
	low[u] = dfn[u] = ++cnt;
	stk.push(u);
	for(auto p : g[u]){
        lt v = p.first;
		if(!dfn[v]){
			son++;
			Tarjan(v, p.second);
			low[u] = min(low[u], low[v]);
			if(low[v] > dfn[u]) cut[p.second] = true;//割边
		}
		else if(p.second != fa) low[u] = min(low[u], dfn[v]);
	}
}

void dfs(lt s, lt dccn){
    dcc[s] = dccn;
    for(auto p : g[s]){
        lt v = p.first;
        if(dcc[v] || cut[p.second]) continue;
        // 如果这个点属于其他分量或者这条边是割边，就停止搜索。
        dfs(v, dccn);
    }
}

int main(){
	int n, m, u, v;
	scanf("%d%d", &n, &m);
	for(int i = 1; i <= m; i++){
		scanf("%d%d", &u, &v);
		g[u].push_back({v, i});
		g[v].push_back({u, i});
		e[i] = (Edge){u, v};
	}
	for(int i = 1; i <= n; i++){
		if(dfn[i] == 0){
			//stk.clear();只能手动清空
			while(!stk.empty()) stk.pop();
			Tarjan(i, 0);
		}
	} 
	int sum = 0;
	for(int i = 1; i <= n; i++){
		if(cut[i]) sum++;
	}
    for(int i = 1; i <= n; i++){
        if(!dcc[i]) dfs(i, ++dccn);
    }
    printf("%lld\n", dccn);
    for(int i = 1; i <= n; i++){
        dccs[dcc[i]].push_back(i);
    }
    for(int i = 1; i <= dccn; i++){
        printf("%d ", dccs[i].size());
        for(lt v : dccs[i]) printf("%lld ", v);
        printf("\n");
    }
	return 0;
}

10. 欧拉回路

作为图论最重要的部分之一，详见影越论欧拉回路篇！

后记

修改记录

$2024.8.11$ —— 第一次整理。
缺失部分：双连通的基本性质；最短路、树上问题、最小生成树、欧拉回路的链接

参考资料

只参考了连通性部分

肺腑

愿君在影越这里受益匪浅，感激不尽！—— $ysl$_$wf$

posted @ 2024-08-11 18:23 元越阅读(15) 评论(2) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

元越

われは鋒の名を以て、三千洲に響き渡る！