动手动脑（一）
1 public class EnumTest { 2 3 public static void main(String[] args) { 4 Size s=Size.SMALL; 5 Size t=Size.LARGE; 6 //s和t引用同一个对象？ 7 System.out.println(s==t); // 8 //是原始数据类型吗？ 9 System.out.println(s.getClass().isPrimitive()); 10 //从字符串中转换 11 Size u=Size.valueOf("SMALL"); 12 System.out.println(s==u); //true 13 //列出它的所有值 14 for(Size value:Size.values()){ 15 System.out.println(value); 16 } 17 } 18 19 } 20 enum Size{SMALL,MEDIUM,LARGE}；
运行结果：
结论：1.枚举类型是引用类型
2.枚举不属于原始数据类型，它的每个具体值都引用一个特定的对象。相同的值则引用同一个对象。
3.可以使用“==”和equals()方法直接比对枚举变量的值，换句话说，对于枚举类型的变量，“==”和equals()方法执行的结果是等价的。
枚举类型的基本用法：1、枚举型常量；2、带一个参数的枚举；3、向枚举中添加新方法；4、覆盖枚举的方法。
二、
代码：
1 public class TestDouble { 2 3 public static void main(String args[]) { 4 System.out.println("0.05 + 0.01 = " + (0.05 + 0.01)); 5 System.out.println("1.0 - 0.42 = " + (1.0 - 0.42)); 6 System.out.println("4.015 * 100 = " + (4.015 * 100)); 7 System.out.println("123.3 / 100 = " + (123.3 / 100)); 8 } 9 }
运行结果：
结论：使用double类型的数值进行计算，其结果是不精确的。
原因：浮点数在计算机中的表示通过特定的格式与规则来进行存储。
解决方法：使用BigDecimal类
代码：
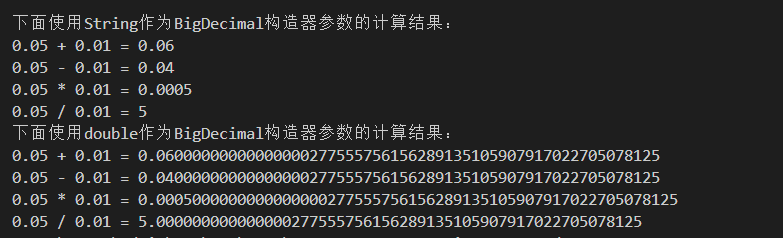
1 import java.math.BigDecimal; 2 3 public class TestBigDecimal 4 { 5 public static void main(String[] args) 6 { 7 BigDecimal f1 = new BigDecimal("0.05"); 8 BigDecimal f2 = BigDecimal.valueOf(0.01); 9 BigDecimal f3 = new BigDecimal(0.05); 10 System.out.println("下面使用String作为BigDecimal构造器参数的计算结果："); 11 System.out.println("0.05 + 0.01 = " + f1.add(f2)); 12 System.out.println("0.05 - 0.01 = " + f1.subtract(f2)); 13 System.out.println("0.05 * 0.01 = " + f1.multiply(f2)); 14 System.out.println("0.05 / 0.01 = " + f1.divide(f2)); 15 System.out.println("下面使用double作为BigDecimal构造器参数的计算结果："); 16 System.out.println("0.05 + 0.01 = " + f3.add(f2)); 17 System.out.println("0.05 - 0.01 = " + f3.subtract(f2)); 18 System.out.println("0.05 * 0.01 = " + f3.multiply(f2)); 19 System.out.println("0.05 / 0.01 = " + f3.divide(f2)); 20 } 21 }
运行结果：
三、
1 public class add{ 2 public static void main(String[] args){ 3 int X=100; 4 int Y=200; 5 System.out.println("X+Y="+X+Y); 6 System.out.println(X+Y+"=X+Y"); 7 } 8 }
运行结果：
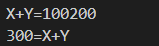
出现此结果的原因： 字符串前面的按原来的格式相加，字符串后面的都按字符串相加
四、原码、反码、补码
在了解原码, 反码和补码之前, 需要先了解机器数和真值的概念.
1.机器数：一个数在计算机中的二进制表示形式, 叫做这个数的机器数。机器数是带符号的，在计算机用一个数的最高位存放符号, 正数为0, 负数为1.
比如，十进制中的数 +3 ，计算机字长为8位，转换成二进制就是00000011。如果是 -3 ，就是 10000011 。
那么，这里的 00000011 和 10000011 就是机器数。
2.真值：因为第一位是符号位，所以机器数的形式值就不等于真正的数值。例如上面的有符号数 10000011，其最高位1代表负，其真正数值是 -3 而不是形式值131（10000011转换成十进制等于131）。所以，为区别起见，将带符号位的机器数对应的真正数值称为机器数的真值。
例：0000 0001的真值 = +000 0001 = +1，1000 0001的真值 = –000 0001 = –1
原码，反码，补码的基础概念和计算方法
1.原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:
[+1]原 = 0000 0001
[-1]原 = 1000 0001
第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:
[1111 1111 , 0111 1111]
即[-127 , 127]
原码是人脑最容易理解和计算的表示方式.
2.反码
反码的表示方法是:
正数的反码是其本身
负数的反码是在其原码的基础上, 符号位不变，其余各个位取反.
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反
可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算.
3. 补码
补码的表示方法是:
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
对于负数, 补码表示方式也是人脑无法直观看出其数值的.通常也需要转换成原码在计算其数值.
原码的缺陷:
使用原码直接进行运算，对于加法是没有问题的
原码最大的问题是，无法将减法转换为加法。例如3-2，我们可以通过计算3+(-2)得到结果，原码的计算结果是-5，明显是错误的。
反码的瑕疵:
反码的出现正是弥补了原码无法执行减法运算的问题，反码运算减法的规则：A-B=A+(-B)，如果最高位发生了进位，则需要低位再加1。
反码的计算结果是对的，但是算法规则稍微有点复杂，需要考虑最高位溢位的情况，效率偏低，另外还有一点瑕疵：0有两种编码。
以1-1为例，反码的计算过程如下，结果为-0，其实也就是0。我们发现，在反码中，00000000和11111111都表示0，0有两种编码，在判断是否为0时需要判断两种编码，算是一点小瑕疵。
补码的完美:
补码是现代计算机使用的编码格式，同时解决了原码的缺陷和反码的瑕疵。
其次，0不再有两种编码了，还是以1-1为例，计算过程如下，0只有一个编码，那就是00000000。既然00000000代表1，那11111111代表什么呢？此时人为的规定它就是-128D，所以使用补码，1个字节的表示范围是[-128,127]，比反码还多了一个数值
