Day 75 数据结构

数据结构

数据结构是指相互之间存在着一种或多种关系的数据元素的集合和该集合中数据元素之间的关系组成。 简单来说，数据结构就是设计数据以何种方式组织并存储在计算机中。 比如：列表、集合与字典等都是一种数据结构。 N.Wirth: “程序=数据结构+算法”。

数据结构的分类

数据结构按照其逻辑结构可分为线性结构、树结构、图结构

线性结构：数据结构中的元素存在一对一的相互关系

树结构：数据结构中的元素存在一对多的相互关系

图结构：数据结构中的元素存在多对多的相互关系

栈

使用一般的列表结构即可实现栈

进栈：li.append

出栈：li.pop

取栈顶：li[-1]

 

 

 

栈的应用——括号匹配问题

括号匹配问题：给一个字符串，其中包含小括号、中括号、大括号，求该字符串中的括号是否匹配。
例如：

()()[]{} 匹配

([{()}]) 匹配

[]( 不匹配

[(]) 不匹配

def match(s):
    match = {'}': '{', ']': '[', ')': '('}
    li = []
    for ch in s:
        if ch in {'{', '(', '['}:
            li.append(ch)
        else:  # ch in {'}',')',']'}
            if len(li) == 0:
                return False
            elif len(li) > 0 and li[-1] == match[ch]:
                li.pop()
            else:  # li[-1] not in match
                return False
    if len(li):
        return False
    else:
        return True


print(match('{[{()}]}'))

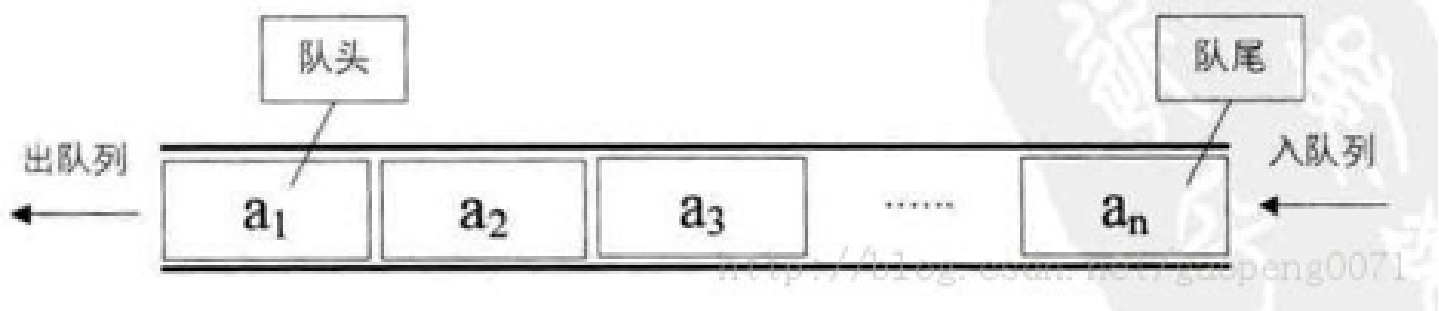
队列

队列(Queue)是一个数据集合，仅允许在列表的一端进行插入，另一端进行删除。

进行插入的一端称为队尾(rear)，插入动作称为进队或入队

进行删除的一端称为队头(front)，删除动作称为出队

队列的性质：先进先出(First-in, First-out)

 

class Queue:
    def __init__(self, size=100):
        self.size = size
        self.queue = [0 for _ in range(100)]
        self.rear = 0  # 队尾指针
        self.front = 0  # 队首指针

    def push(self, element):
        if not self.is_filled():
            self.rear = (self.rear + 1) % self.size
            self.queue[self.rear] = element
        else:
            raise ImportError('队列已满')

    def pop(self):
        if not self.is_empth():
            self.front = (self.front + 1) % self.size
            return self.queue[self.front]
        else:
            raise ImportError('队列已空')

    # 判断队空
    def is_empth(self):
        return self.rear == self.front

    # 判断队满
    def is_filled(self):
        return (self.rear + 1) % self.size == self.front



q = Queue(5)
for i in range(4):
    q.push(i)

print(q.is_filled())
print(q.pop())
print(q.pop())
print(q.pop())
print(q.pop())
print(q.push(15))
print(q.pop())

 

双向队列

双向队列的两端都支持进队和出队操作

双向队列的基本操作： 队首进队、队首出队、队尾进队、队尾出队

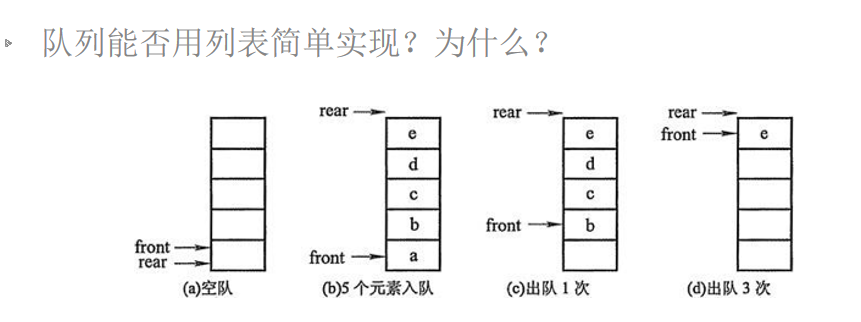
队列的实现

from collections import deque
q = deque([1,2,3,4,5],5) # 非空对列 长度为 5，长度大于 5 时，会自动八队首移出
q.append(7)         # 队尾进队
print(q.popleft())  # 队首出队

q.appendleft(1)     # 队首进队
print(q.pop())      # 队尾出对

# 读取文件中后 5 行数据
def tail(num):
    with open('./info.txt','r',encoding='utf-8')as f:
        q = deque(f,num)
        return q

for i in tail(5):
    print(i,end='')

 

队列的实现方式——环形队列

 

 

 

 栈和队列的应用——迷宫问题

 

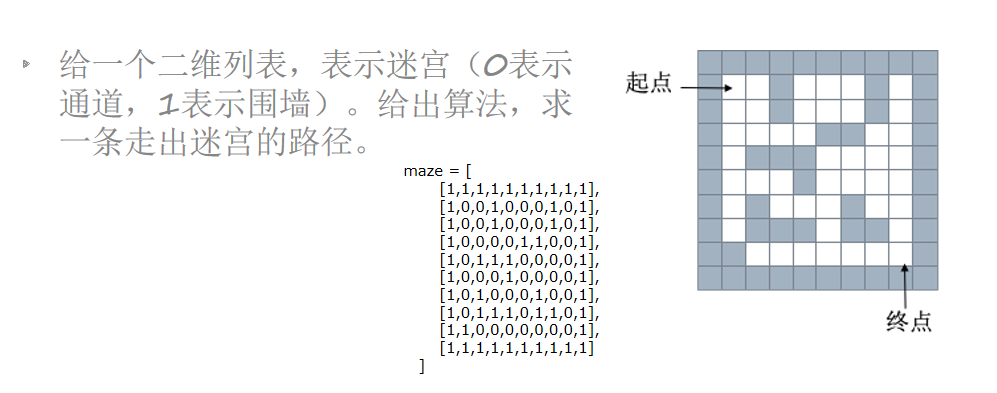
栈——深度优先搜索

 

# 0 代表路，1 代表墙
maze = [
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
    [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
    [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
    [1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
    [1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
    [1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
    [1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]

# 方向
dirs = [
    lambda x, y: (x + 1, y),
    lambda x, y: (x - 1, y),
    lambda x, y: (x, y + 1),
    lambda x, y: (x, y - 1),
]


def maze_path(x1, y1, x2, y2):
    stack = []
    stack.append((x1, y1))
    while len(stack) > 0:
        curCode = stack[-1]  # 当前节点
        if curCode[0] == x2 and curCode[1] == y2:
            # 走到了终点
            for p in stack:
                print(p)
            return True
        # 查找 4 个方向
        for dir in dirs:
            nextCode = dir(curCode[0], curCode[1])
            if maze[nextCode[0]][nextCode[1]] == 0:
                stack.append(nextCode)
                maze[nextCode[0]][nextCode[1]] = 2  # 表示已经走过了
                break
        else:
            maze[nextCode[0]][nextCode[1]] = 2
            stack.pop()

    else:
        print('没有路')
        return False

maze_path(1,1,8,8)

 

队列——广度优先搜索

 

from collections import deque

# 0 代表路，1 代表墙
maze = [
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1],
    [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
    [1, 0, 0, 1, 0, 0, 0, 1, 0, 1],
    [1, 0, 0, 0, 0, 1, 1, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 0, 0, 0, 1],
    [1, 0, 0, 0, 1, 0, 0, 0, 0, 1],
    [1, 0, 1, 0, 0, 0, 1, 0, 0, 1],
    [1, 0, 1, 1, 1, 0, 1, 1, 0, 1],
    [1, 1, 0, 0, 0, 0, 0, 0, 0, 1],
    [1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
]

# 方向
dirs = [
    lambda x, y: (x + 1, y),
    lambda x, y: (x - 1, y),
    lambda x, y: (x, y + 1),
    lambda x, y: (x, y - 1),
]

def print_r(path):
    real_path = []
    i = len(path) - 1
    while i >= 0:
        real_path.append(path[i][0:2])
        i = path[i][2]
    real_path.reverse()
    for node in real_path:
        print(node)


def maze_path_duque(x1, y1, x2, y2):
    queue = deque()
    path = []
    queue.append((x1,y1,-1))    # 设置起点坐标
    while len(queue) > 0:        # 当队列不为空循环
        cur_node = queue.popleft()
        path.append(cur_node)
        if cur_node[0] == x2 and cur_node[1] == y2:
            print_r(path)     # 到达终点 打印坐标
            return True

        for dir in dirs:
            next_node = dir(cur_node[0],cur_node[1])
            if maze[next_node[0]][next_node[1]] == 0:
                queue.append((next_node[0],next_node[1],len(path) - 1))
                maze[next_node[0]][next_node[1]] = 2  # 走过的路径

    return False

maze_path_duque(1,1,8,8)

链表

 

 

 

创建与遍历链表

class Node:
    def __init__(self,item):
        self.item = item
        self.next = None


# a = Node(1)
# b = Node(2)
# a.next = b
# print(a.next.item)

# 头插法
def create_linklist_head(li):
    head = Node(li[0])      # 创建空列表，设置头节点
    for val in li[1:]:
        node = Node(val)
        node.next = head
        head = node
    return head

# 尾插法
def create_linklist_tail(li):
    head = Node(li[0])
    tail = head
    for val in li[1:]:
        node = Node(val)
        tail.next = node
        tail = node
    return head


def look(lk):
    while lk:
        print(lk.item,end=',')
        lk = lk.next

# lk_head = create_linklist_head([1,2,3,4,5])
lk_tail = create_linklist_tail([1,2,3,4,5])
print(look(lk_tail))

链表的插入和删除

 

 

 

 

 

 

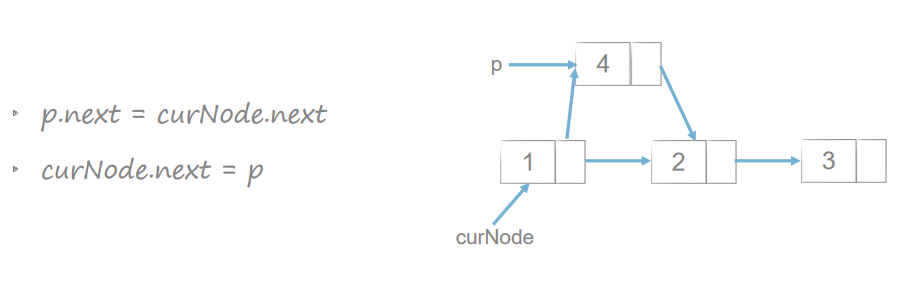
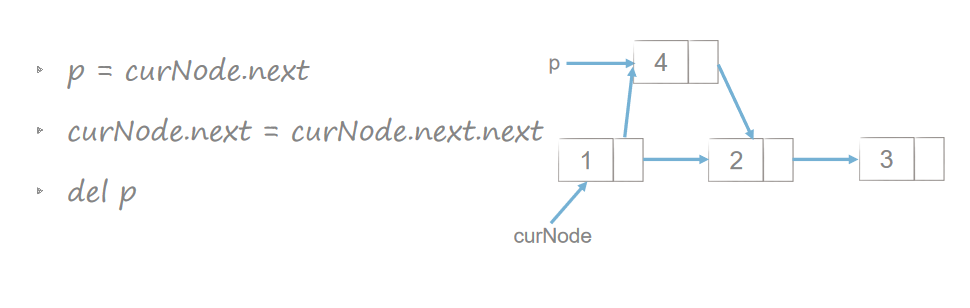
双链表

 

 

双链表的插入与删除

 

 

 

 

 

 

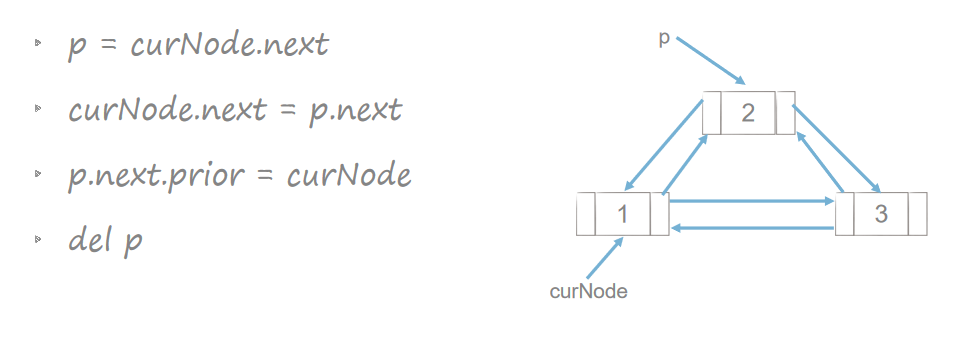
链表在插入和删除的操作上明显快于顺序表

链表的内存可以更灵活的分配，试利用链表重新实现栈和队列

链表这种链式存储的数据结构对树和图的结构有很大的启发性

 

哈希表

哈希表一个通过哈希函数来计算数据存 储位置的数据结构，通常支持如下操作：

insert(key, value)：插入键值对

(key,value) get(key)：如果存在键为key的键值对则返回其value，否则返回空值

delete(key)：删除键为key的键值对

直接寻址表

 

 

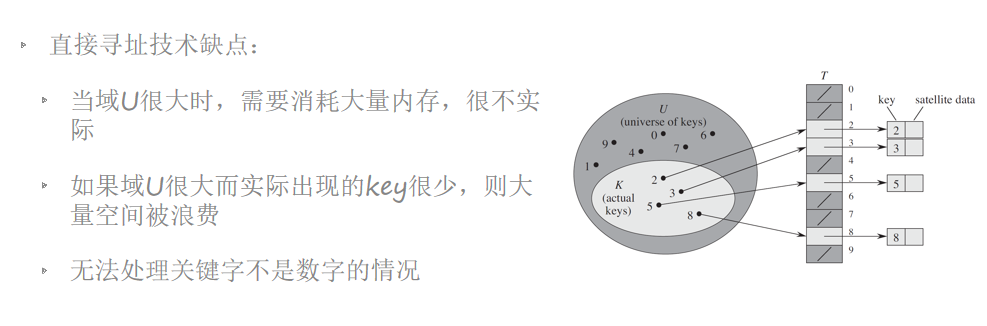
哈希

 

 

 

 

哈希冲突

 

 

 

 

 

 

 

 

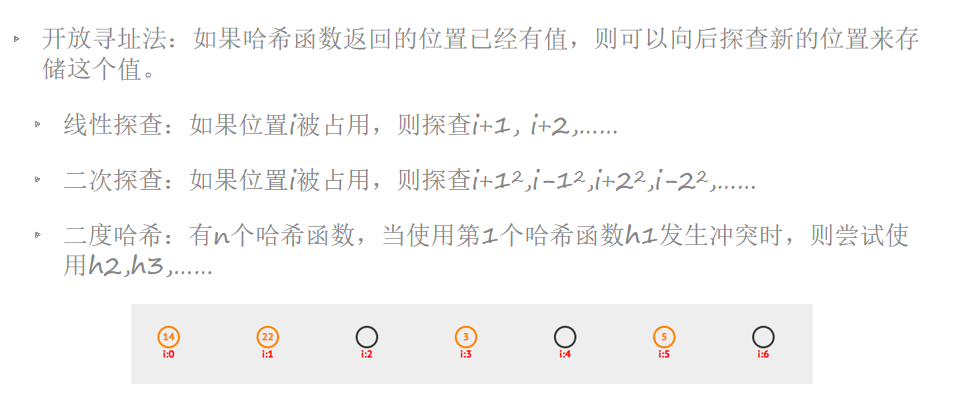
 哈希表——常见哈希函数

除法哈希法： h(k) = k % m

乘法哈希法： h(k) = floor(m*(A*key%1))

全域哈希法： ha,b(k) = ((a*key + b) mod p) mod m a,b=1,2,...,p-1

class LinkList:
    class Node:
        def __init__(self, item=None):
            self.item = item
            self.next = None

    class LinkListIterator:
        def __init__(self, node):
            self.node = node

        def __next__(self):
            if self.node:
                cur_node = self.node
                self.node = cur_node.next
                return cur_node.item
            else:
                raise StopIteration

        def __iter__(self):
            return self

    def __init__(self, iterable=None):
        self.head = None
        self.tail = None
        if iterable:
            self.extend(iterable)

    def append(self, obj):
        s = LinkList.Node(obj)
        if not self.head:
            self.head = s
            self.tail = s
        else:
            self.tail.next = s
            self.tail = s

    def extend(self, iterable):
        for obj in iterable:
            self.append(obj)

    def find(self, obj):
        for n in self:
            if n == obj:
                return True
        else:
            return False

    def __iter__(self):
        return self.LinkListIterator(self.head)

    def __repr__(self):
        return "<<"+", ".join(map(str, self))+">>"

# 类似于集合的结构
class HashTable:
    def __init__(self, size=101):
        self.size = size
        self.T = [LinkList() for i in range(self.size)]

    def h(self, k):
        return k % self.size

    def insert(self, k):
        i = self.h(k)
        if self.find(k):
            print("Duplicated Insert.")
        else:
            self.T[i].append(k)

    def find(self, k):
        i = self.h(k)
        return self.T[i].find(k)


ht = HashTable()

ht.insert(0)
ht.insert(1)
ht.insert(3)
ht.insert(102)
ht.insert(508)

#print(",".join(map(str, ht.T)))
print(ht.find(203))

哈希表的应用——集合与字典

字典与集合都是通过哈希表来实现的。

a = {'name': 'Alex', 'age': 18, 'gender': 'Man'}

使用哈希表存储字典，通过哈希函数将字典的键映射为下标。假设h('name') = 3, h('age') = 1, h('gender') = 4，则哈希表存储为[None, 18, None, 'Alex', 'Man']

如果发生哈希冲突，则通过拉链法或开发寻址法解决

 

Python对字典的关键字有什么要求？如何使一个自定义的类的对象成为字典的键？

Python对集合中的元素有什么要求？如何利用集合对大量的对象去重？

 

树的实例：模拟文件系统

class Node:
    def __init__(self, name, type='dir'):
        self.name = name
        self.type = type   #"dir" or "file"
        self.children = []
        self.parent = None
        # 链式存储

    def __repr__(self):
        return self.name


class FileSystemTree:
    def __init__(self):
        self.root = Node("/")
        self.now = self.root

    def mkdir(self, name):
        # name 以 / 结尾
        if name[-1] != "/":
            name += "/"
        node = Node(name)
        self.now.children.append(node)
        node.parent = self.now

    def ls(self):
        return self.now.children

    def cd(self, name):
        # "/var/python/"
        if name[-1] != "/":
            name += "/"
        if name == "../":
            self.now = self.now.parent
            return
        for child in self.now.children:
            if child.name == name:
                self.now = child
                return
        raise ValueError("invalid dir")



tree = FileSystemTree()
tree.mkdir("var/")
tree.mkdir("bin/")
tree.mkdir("usr/")

tree.cd("bin/")
tree.mkdir("python/")

tree.cd("../")

print(tree.ls())

 

二叉树

二叉树的链式存储：将二叉树的节点定义为一个对象，节点之间通过类似链表的链接方式来连接。

二叉树遍历

from collections import deque

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None  # 左孩子
        self.rchild = None  # 右孩子

a = BiTreeNode('A')
b = BiTreeNode('B')
c = BiTreeNode('C')
d = BiTreeNode('D')
e = BiTreeNode('E')
f = BiTreeNode('F')
g = BiTreeNode('G')

root = e
e.lchild = a
e.rchild = g
a.rchild = c
c.lchild = b
c.rchild = d
g.rchild = f

# print(root.rchild.rchild.data)


# 前序遍历
def front_order(root):
    if root:
        print(root.data,end=',')
        front_order(root.lchild)
        front_order(root.rchild)
# front_order(root)

# 中序遍历
def middle_order(root):
    if root:
        middle_order(root.lchild)
        print(root.data,end=',')
        middle_order(root.rchild)

# middle_order(root)

# 后序遍历
def back_order(root):
    if root:
        middle_order(root.lchild)
        print(root.data, end=',')
        middle_order(root.rchild)

# middle_order(root)

# 层级遍历
def level_order(root):
    qu = deque()
    qu.append(root)
    while len(qu)>0:
        node = qu.popleft()
        print(node.data,end=',')
        if node.lchild:
            qu.append(node.lchild)
        if node.rchild:
            qu.append(node.rchild)


level_order(root)

 

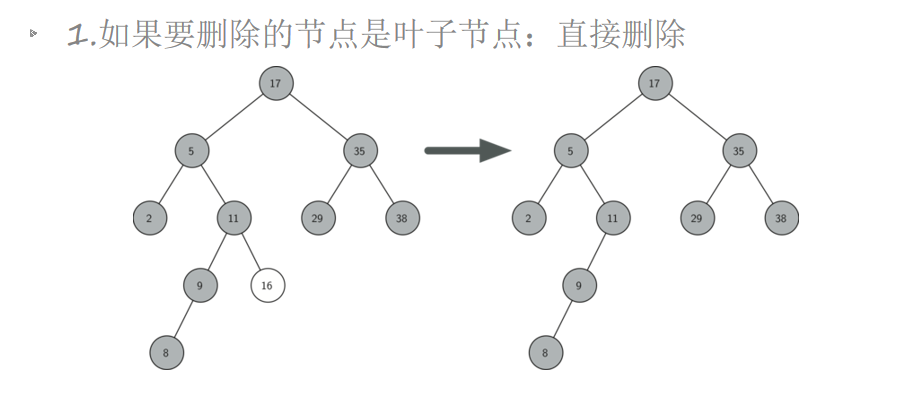
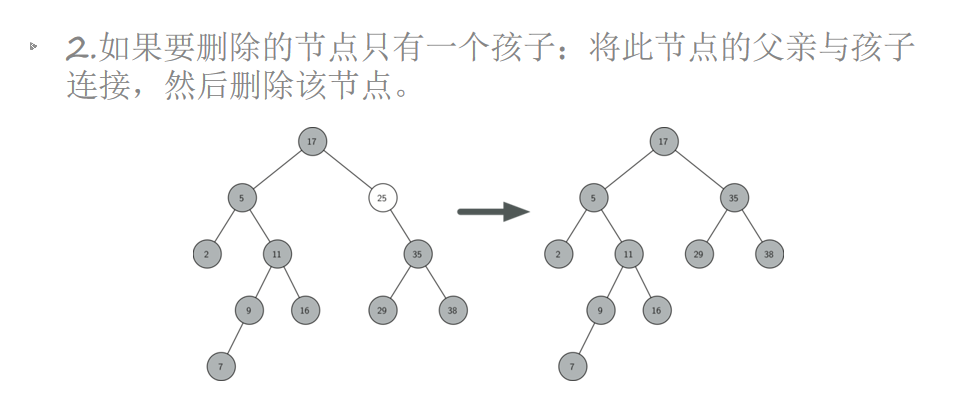
二叉树：插入、查询、删除

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

import random

class BiTreeNode:
    def __init__(self, data):
        self.data = data
        self.lchild = None   # 左孩子
        self.rchild = None  # 右孩子
        self.parent = None

class BST:
    def __init__(self, li=None):
        self.root = None
        if li:
            for val in li:
                self.insert_no_rec(val)

    def insert(self, node, val):
        if not node:
            node = BiTreeNode(val)
        elif val < node.data:
            node.lchild = self.insert(node.lchild, val)
            node.lchild.parent = node
        elif val > node.data:
            node.rchild = self.insert(node.rchild, val)
            node.rchild.parent = node
        return node

    def insert_no_rec(self, val):
        p = self.root
        if not p:               # 空树
            self.root = BiTreeNode(val)
            return
        while True:
            if val < p.data:
                if p.lchild:
                    p = p.lchild
                else:           # 左孩子不存在
                    p.lchild = BiTreeNode(val)
                    p.lchild.parent = p
                    return
            elif val > p.data:
                if p.rchild:
                    p = p.rchild
                else:
                    p.rchild = BiTreeNode(val)
                    p.rchild.parent = p
                    return
            else:
                return

    def query(self, node, val):
        if not node:
            return None
        if node.data < val:
            return self.query(node.rchild, val)
        elif node.data > val:
            return self.query(node.lchild, val)
        else:
            return node

    def query_no_rec(self, val):
        p = self.root
        while p:
            if p.data < val:
                p = p.rchild
            elif p.data > val:
                p = p.lchild
            else:
                return p
        return None

    def pre_order(self, root):
        if root:
            print(root.data, end=',')
            self.pre_order(root.lchild)
            self.pre_order(root.rchild)

    def in_order(self, root):
        if root:
            self.in_order(root.lchild)
            print(root.data, end=',')
            self.in_order(root.rchild)

    def post_order(self, root):
        if root:
            self.post_order(root.lchild)
            self.post_order(root.rchild)
            print(root.data, end=',')


    def __remove_node_1(self, node):
        # 情况1：node是叶子节点
        if not node.parent:
            self.root = None
        if node == node.parent.lchild:  #node是它父亲的左孩子
            node.parent.lchild = None
        else:   #右孩子
            node.parent.rchild = None

    def __remove_node_21(self, node):
        # 情况2.1：node只有一个左孩子
        if not node.parent: # 根节点
            self.root = node.lchild
            node.lchild.parent = None
        elif node == node.parent.lchild:
            node.parent.lchild = node.lchild
            node.lchild.parent = node.parent
        else:
            node.parent.rchild = node.lchild
            node.lchild.parent = node.parent

    def __remove_node_22(self, node):
        # 情况2.2：node只有一个右孩子
        if not node.parent:
            self.root = node.rchild
        elif node == node.parent.lchild:
            node.parent.lchild = node.rchild
            node.rchild.parent = node.parent
        else:
            node.parent.rchild = node.rchild
            node.rchild.parent = node.parent


    def delete(self, val):
        if self.root:   # 不是空树
            node = self.query_no_rec(val)
            if not node: # 不存在
                return False
            if not node.lchild and not node.rchild: #1. 叶子节点
                self.__remove_node_1(node)
            elif not node.rchild:       # 2.1 只有一个左孩子
                self.__remove_node_21(node)
            elif not node.lchild:       # 2.2 只有一个右孩子
                self.__remove_node_22(node)
            else:   # 3. 两个孩子都有
                min_node = node.rchild
                while min_node.lchild:
                    min_node = min_node.lchild
                node.data = min_node.data
                # 删除min_node
                if min_node.rchild:
                    self.__remove_node_22(min_node)
                else:
                    self.__remove_node_1(min_node)




#
#
# tree = BST([1,4,2,5,3,8,6,9,7])
# tree.in_order(tree.root)
# print("")
#
# tree.delete(4)
# tree.delete(1)
# tree.delete(8)
# tree.in_order(tree.root)

 

AVL树

 

 

 

AVL树——插入

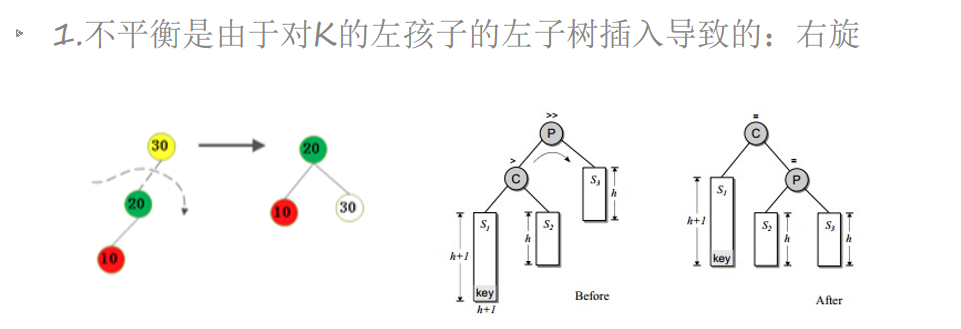
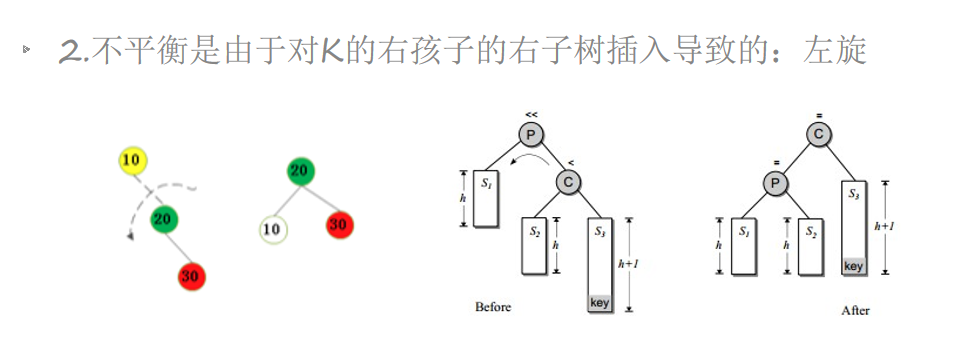
插入一个节点可能会破坏AVL树的平衡，可以通过旋转操作来进行修正。

插入一个节点后，只有从插入节点到根节点的路径上的节点的平衡可能被改变。我们需要找出第一个破坏了平衡条件的节点，称之为K。K的两颗子树的高度差2。

不平衡的出现可能有4种情况

AVL插入——右旋

 

 

 

AVL插入——左旋

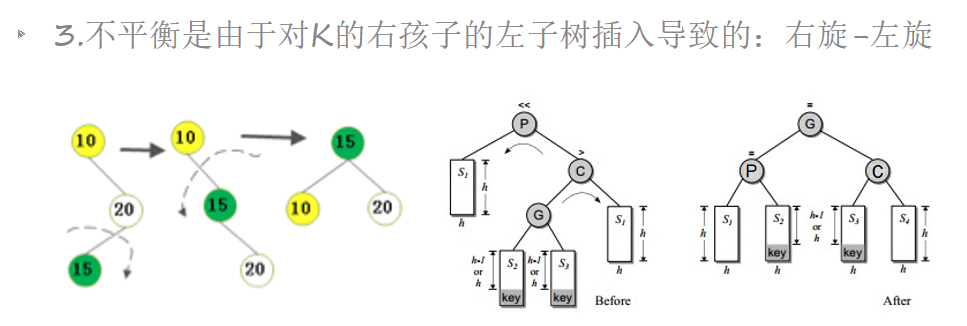
AVL插入——右旋-左旋

 

 

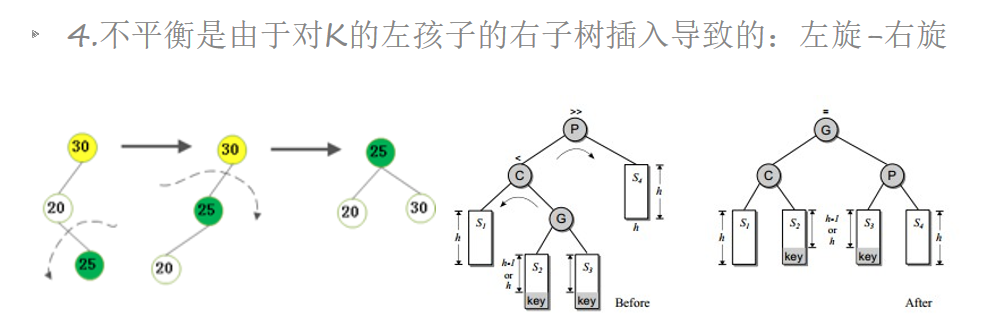
AVL插入——左旋-右旋

 

 

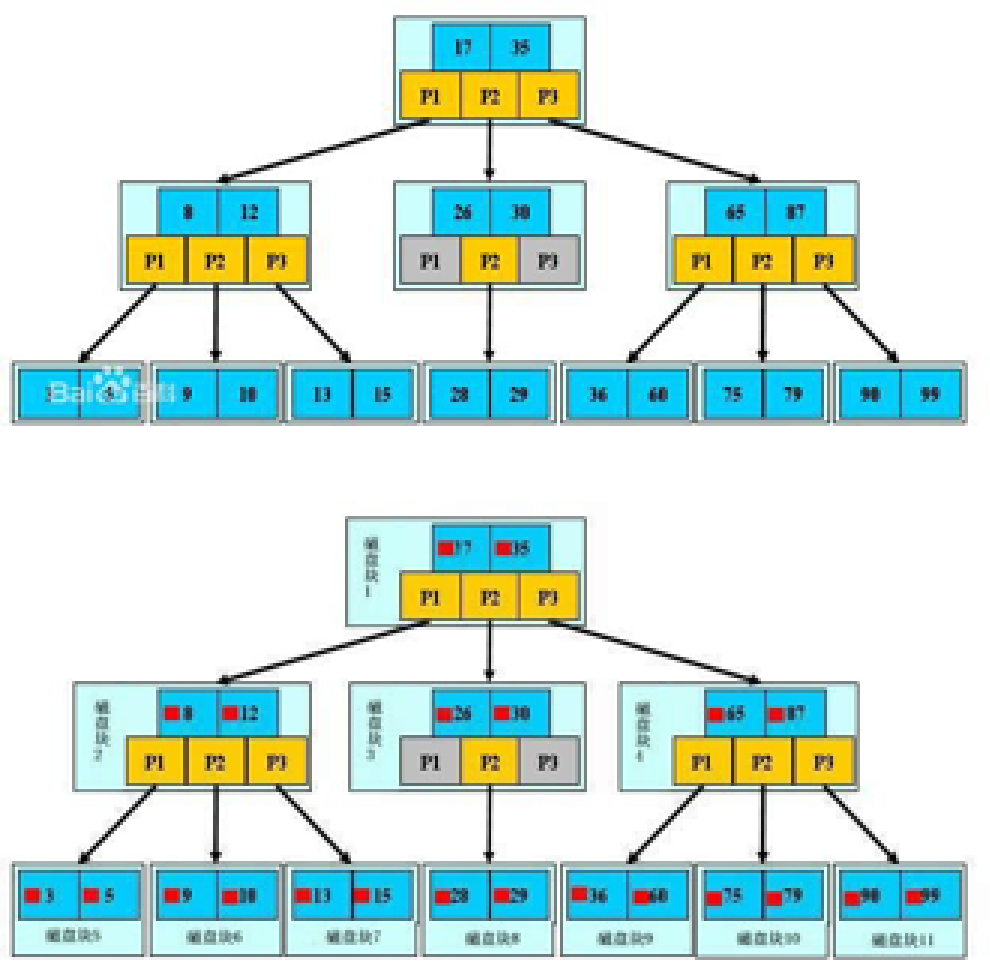
 二叉搜索树扩展应用——B树

B树(B-Tree)：B树是一棵自平衡的多路搜索树。常用于数据库的索引。