Day 74 算法基础(二)
算法基础(二)
列表排序

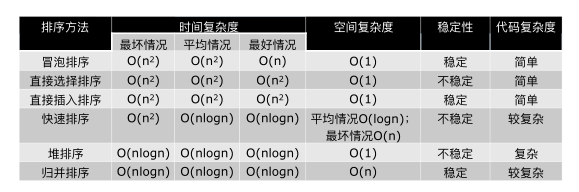
常见排序算法

冒泡排序 (Bubble Sort)

时间复杂度:O(n 2 )
import random def bubble_sort(li): for i in range(len(li) - 1): for k in range(len(li) - i - 1): if li[k] > li[k + 1]: li[k], li[k + 1] = li[k + 1], li[k] li = [random.randint(0,10000) for i in range(100)] print(li) bubble_sort(li) print(li)
冒泡排序-优化
如果冒泡排序中的一趟排序没有发生交换,则说明列表已经有序,可以直接结束算法。
import random def bubble_sort(li): for i in range(len(li) - 1): exchange = False for k in range(len(li) - i - 1): if li[k] > li[k + 1]: li[k], li[k + 1] = li[k + 1], li[k] exchange = True print(li) if not exchange: return li = [9,8,7,1,2,3,4,5,6] bubble_sort(li)
选择排序 (Select Sort)

时间复杂度:O(n 2 )
简单的选择排序
def select_sort_simple(li): li_new = [] for i in range(len(li)): min_val = min(li) li_new.append(min_val) li.remove(min_val) print(li_new) li = [5,6,7,8,9,1,2,3,4,1] select_sort_simple(li)
选择排序
def select_sort(li): for i in (range(len(li) - 1)): min_loc = i for j in range(i + 1, len(li)): if li[j] < li[min_loc]: li[j], li[min_loc] = li[min_loc], li[j] print(li) li = [5, 6, 7, 8, 9, 1, 2, 3, 4, 1] select_sort(li) print(li)
插入排序

时间复杂度:O(n 2 )
def insert_sort(li): for i in range(1, len(li)): # 表示摸到牌的下标 tem = li[i] j = i - 1 # 指手里牌的下标 while j >= 0 and tem < li[j]: li[j + 1] = li[j] j = j - 1 li[j + 1] = tem li = [5, 6, 7, 8, 9, 1, 2, 3, 4, 1] insert_sort(li) print(li)
快速排序


def partition(li, left, right): tem = li[left] while left < right: while left < right and li[right] >= tem: # 从右边找到比 tem 小的数 right -= 1 # 往左移动一位 li[left] = li[right] # 右边的值写到左边的位置上 while left < right and li[left] <= tem: left += 1 li[right] = li[left] li[left] = tem return left def quick_sort(data,left,right): if left < right: min = partition(data, left, right) quick_sort(data, min + 1, right) quick_sort(data, left, min - 1) li = [5, 6, 7, 8, 9, 1, 2, 3, 4, 1] quick_sort(li, 0, len(li) - 1) print(li)
堆排序
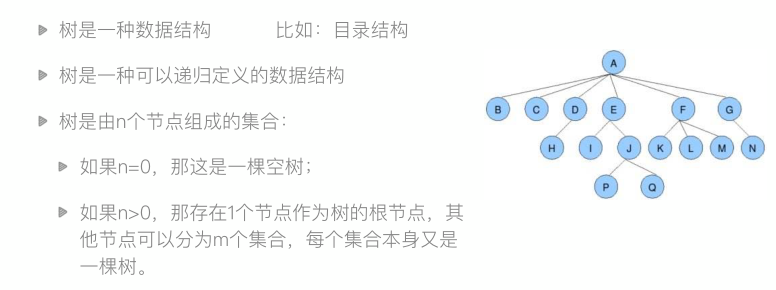
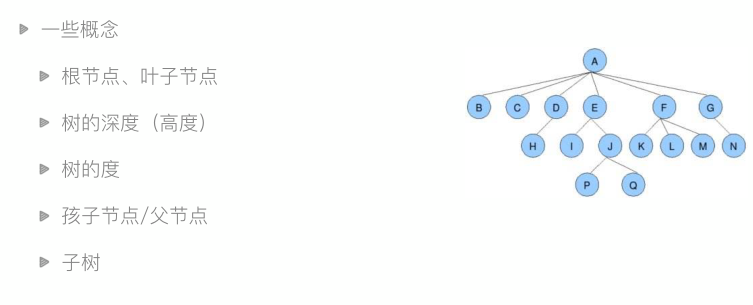
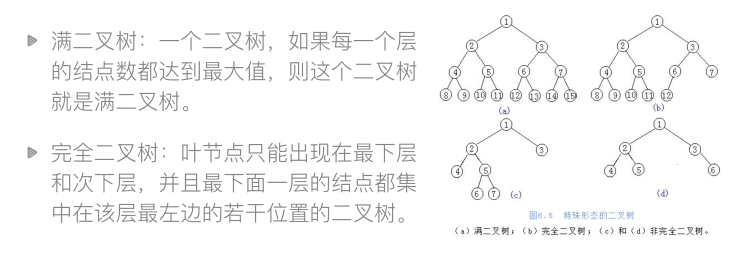
堆排序前传-树与二叉树



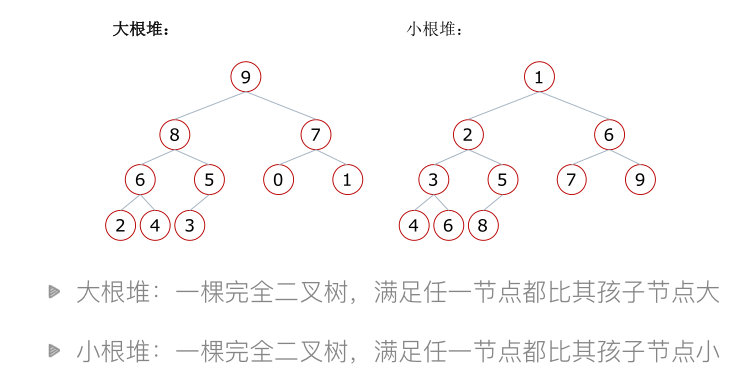
堆排序——什么是堆



def sift(li, low, high): ''' :param li: 列表 :param low: 堆的根节点位置 :param high: 堆的最后一个元素的位置 :return: ''' i = low # i 是最开始指向的跟节点 j = 2 * i + 1 # j 是左孩子 tmp = li[low] # 把堆顶存起来 while j <= high: # 只要 j 位置有数 if j + 1 <= high and li[j + 1] > li[j]: # 如果右孩子存在且比左孩子大 j = j + 1 # j 指向右孩子 if li[j] > tmp: # 右孩子大于 tmp li[i] = li[j] # 把右孩子放到 i 的位置 i = j # 往下看一层,更新 i j = 2 * i + 1 # 往下看一层,更新 j else: # tmp 更大,把 tmp 放到 i 的位置上 li[i] = tmp # 把 tmp 放到某一级的领导的位置上 break else: li[i] = tmp # 把 tmp 放到某一级的领导的位置上 def heap_sort(li): n = len(li) # 获取到列表的长度 # 建堆 for i in range((n - 2) // 2, -1, -1): # i 表示建堆的时候调整的部分的根的下标 sift(li, i, n - 1) # 挨个出数 for i in range(n - 1, -1, -1): # i 指向当前堆的最后一个元素 li[0], li[i] = li[i], li[0] sift(li, 0, i - 1) # i-1 是新的 high import random li = [i for i in range(100)] random.shuffle(li) print(li) heap_sort(li) print(li)
堆排序——内置模块

import heapq, random li = list(range(100)) random.shuffle(li) print(li) # 建堆 heapq.heapify(li) # 出最小的数 for i in range(len(li)): print(heapq.heappop(li), end=',')
堆排序——topk问题


def sift(li, low, high): ''' :param li: 列表 :param low: 堆的根节点位置 :param high: 堆的最后一个元素的位置 :return: ''' i = low # i 是最开始指向的跟节点 j = 2 * i + 1 # j 是左孩子 tmp = li[low] # 把堆顶存起来 while j <= high: # 只要 j 位置有数 if j + 1 <= high and li[j + 1] < li[j]: # 如果右孩子存在且比左孩子大 j = j + 1 # j 指向右孩子 if li[j] < tmp: # 右孩子大于 tmp li[i] = li[j] # 把右孩子放到 i 的位置 i = j # 往下看一层,更新 i j = 2 * i + 1 # 往下看一层,更新 j else: # tmp 更大,把 tmp 放到 i 的位置上 li[i] = tmp # 把 tmp 放到某一级的领导的位置上 break else: li[i] = tmp # 把 tmp 放到某一级的领导的位置上 def topk(li, k): heap = li[0:k] for i in range((k - 2) // 2, -1, -1): sift(heap, i, k - 1) # 建堆 for i in range(k, len(li) - 1): if li[i] > heap[0]: heap[0] = li[i] sift(heap, 0, k - 1) # 遍历 for i in range(k - 1, -1, -1): heap[0], heap[i] = heap[i], heap[0] sift(heap, 0, i - 1) return heap import random li = list(range(1000)) random.shuffle(li) print(topk(li, 10))
归并排序


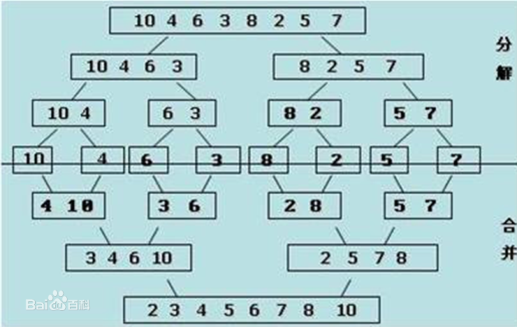
def merge(li, low, mid, high): i = low j = mid + 1 ltem = [] while i <= mid and j <= high: # 保证两边都有数 if li[i] < li[j]: ltem.append(li[i]) i += 1 else: ltem.append(li[j]) j += 1 while i <= mid: ltem.append(li[i]) i += 1 while j <= high: ltem.append(li[j]) j += 1 li[low:high + 1] = ltem def merge_sort(li, low, high): if low < high: mid = (low + high) // 2 merge_sort(li, low, mid) merge_sort(li, mid + 1, high) merge(li, low, mid, high) import random li = list(range(100)) random.shuffle(li) merge_sort(li, 0, len(li) - 1) print(li)

希尔排序
希尔排序的时间复杂度讨论比较复杂,并且和选取的gap序列有关。

def insert_sort_gap(li, gap): for i in range(gap, len(li) - 1): tem = li[i] j = i - gap while j >= 0 and li[j] > tem: li[j + gap] = li[j] j -= gap li[j + gap] = tem def shell_sort(li): d = len(li) // 2 while d >= 1: insert_sort_gap(li, d) d //= 2 li = list(range(100)) random.shuffle(li) shell_sort(li) print(li)
计数排序
对列表进行排序,已知列表中的数范围都在0到100之间。设计时间复杂度为O(n)的算法。
def count_sort(li,max_count = 100): count = [0 for _ in range(100 + 1)] # 生成一个列表 for val in li: count[val] += 1 li.clear() for ind,val in enumerate(count): for i in range(val): li.append(ind) li = list(range(100)) random.shuffle(li) count_sort(li) print(li)
桶排序


基数排序
时间复杂度:O(kn)
空间复杂度:O(k+n)
k表示数字位数

def list_to_buckets(li, base, iteration): buckets = [[] for _ in range(base)] for number in li: digit = (number // (base ** iteration)) % base buckets[digit].append(number) return buckets def buckets_to_list(buckets): return [x for bucket in buckets for x in bucket] def radix_sort(li, base=10): maxval = max(li) it = 0 while base ** it <= maxval: li = buckets_to_list(list_to_buckets(li, base, it)) it += 1 return li
查找排序相关面试题






 浙公网安备 33010602011771号
浙公网安备 33010602011771号