Day 73 算法基础

算法基础

算法

算法（Algorithm）：⼀一个计算过程，解决问题的⽅方法

Niklaus Wirth: “程序=数据结构+算法”

 

 时间复杂度

 

 

 

 

 

 

 

 

 

 

 

 

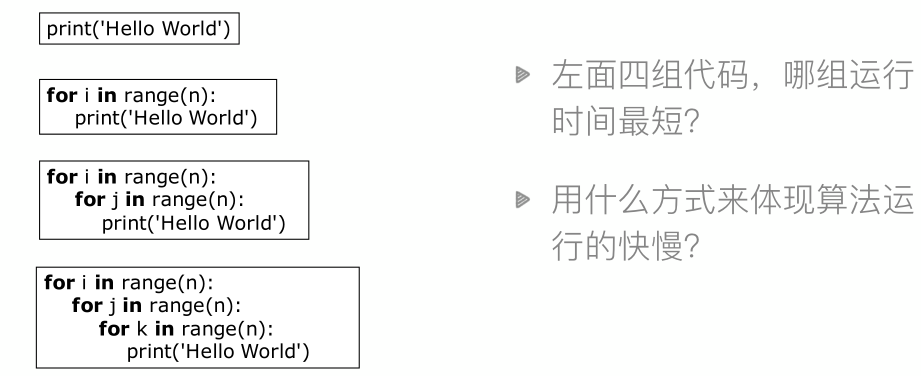
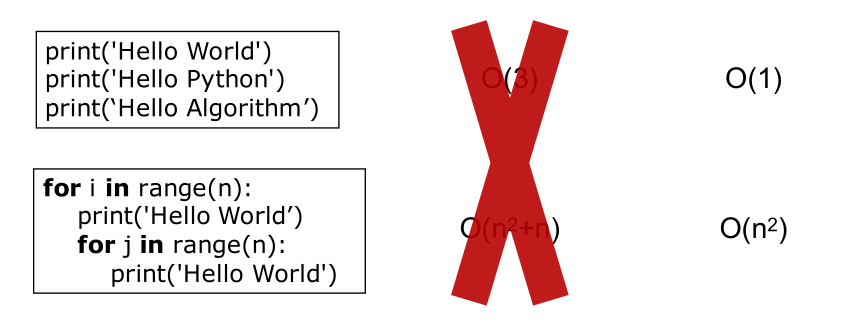
空间复杂度

 

 

 递归

 

 递归实例：汉诺塔问题

 

 

 

 

 

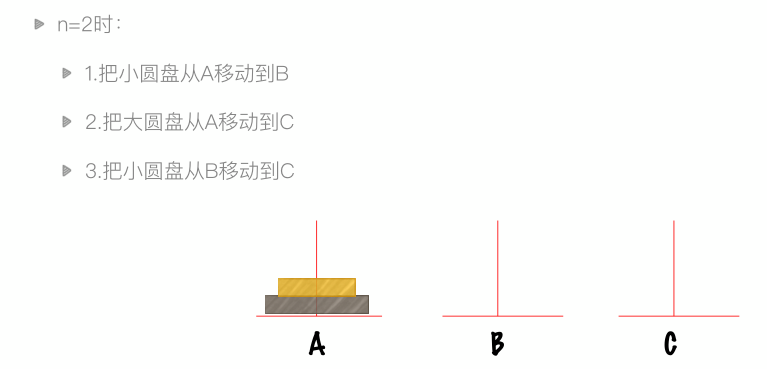
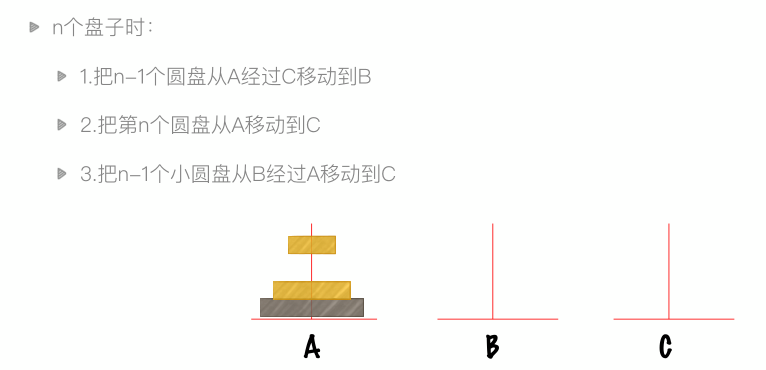
def hanoi(n, a, b, c):
    if n > 0:
    hanoi(n-1, a, c, b)
    print("#%d: moving from %s to %s." % (num, a, c))
    hanoi(n-1, b, a, c)

 

列表查找

查找

 

 顺序查找 (Linear Search)

 

 二分查找 (Binary Searh)

二分查找：又叫折半查找，从有序列表的初始候选区li[0:n]开始，通过对待查找的值与候选区中间值的比较，可以使候选区减少一半。时间复杂度：O(logn)。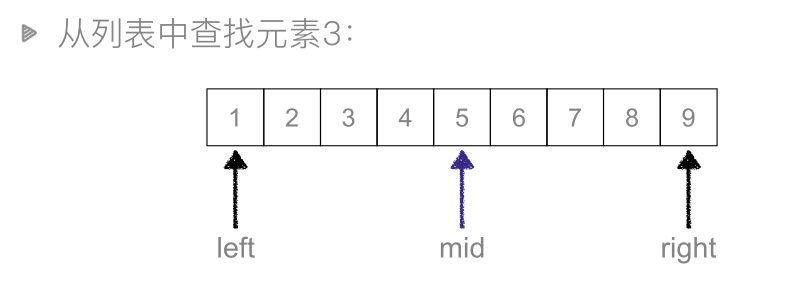

 

 

def binary_search(li, val):
    left = 0
    rigth = len(li) - 1
    while left <= rigth:  # 判断是否有值
        mid = (left + rigth) // 2
        if li[mid] == val:
            return mid
        elif li[mid] > val:  # 待查找的值在 mid 左侧
            rigth = mid - 1
        else:  # 待查找的值在 mid 右侧
            left = mid + 1
    else:
        return None


li = [1, 2, 3, 4, 5, 6, 7, 8, 9]
print(binary_search(li, 3))