AVLTree的Python实现
AVLTree
自己最近在学习数据结构,花了几天理解了下AVLTree的实现,简单一句话概括就是先理解什么是旋转,然后弄明白平衡因子在各种旋转后是如何变化的。最后整理了下学习的过程,并尽量用图片解释,代码水平请高手看到别笑话,有逻辑错误也欢迎指出,谢谢。
简单目录结构:
介绍:
AVL树称为自平衡二叉查找树, 也称为高度平衡二叉搜索树。与普通的二叉搜索树(BST)相比,它能尽量保持子树的高度差不超过2,以减少搜索的时间。
相关概念:
树的高度: 高度是指树节点的最大层次。
AVL树的高度差: 是指在avl树中,任意子树的左右节点的高度差不能超过1
平衡因子: blance factor(bf)指代某个节点左右子树的高度差,即左子树减去右子树的高度,值区间为[-1,0,1]。
搜索效率: AVL树的插入删除查找时间复杂度都为log2N
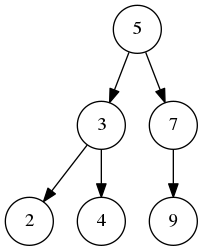
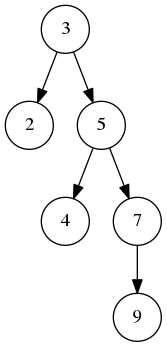
AVL树 BST树
插入实现细节
介绍插入之前先说明每个节点的定义:
class Node(object): def __init__(self, key, parent=None, left=None, right=None): self.key = key # 存储的数据 self.parent = parent # 父节点 self.left = left # 左孩子节点 self.right = right # 右孩子节点 self.bf = 0 # 平衡因子 等于左子树高度减去右子树高度
旋转
旋转是AVL树最重要的操作了,理解了旋转就理解了AVL树的实现原理。
左单旋转
下图节点上面的数字表示平衡因子
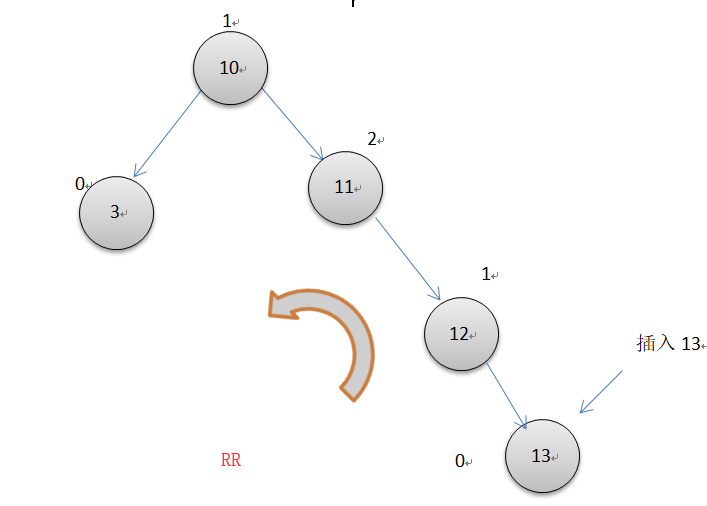

如上图所示: 插入13后,右边子树11节点的平衡因子变为了2(左右节点的高度差), 整个avl树开始不平衡,这时便要开始以12为轴心进行一次左单旋转。具体旋转的操作是原来11的父节点10指向12,12的左节点指向11,而11的右节点指向原来12的左节点(此例中,12的左节点为空)。
说明一下自己对左旋转后,主要操作的两个节点12和11的平衡因子为啥一定是0的理解。
假设原来12节点的左子节点的高度为a, 那么根据平衡因子为1可知,12的右子节点高度为a+1,11的右子节点高度为a+2,此时11的左子节点高度则为a, 发生左单旋转后,11的左子节点高度没变仍为a,11的右子节点指向了原来的12的左子节点,高度为a,所以11的平衡因子则为0,而12的平衡因子等于左边子树1+节点11的高度a减去12的右子节点高度a+1,所以12平衡因子也为0。
def l_rotate(self, par, cur): """ 左单旋转 :param par: 平衡因子为2|-2的节点 :param cur: 作为轴心旋转的节点(平衡因子不为2) :return: None """ p = cur.left # 辅助引用p指向cur的左节点 cur.left = par # cur的左节点指向par par.right = p # par的右节点指向cur的左节点 if p: p.parent = par # cur的左节点不为空时更新该节点的父节点 if par == self.root: self.root = cur # 判断平衡因子为2的par是否为根 else: if par == par.parent.left: # 更新par父节点的子节点信息 par.parent.left = cur else: par.parent.right = cur cur.parent = par.parent # 当前cur的父节点指向原来par的父节点 par.parent = cur # par变为cur的左子节点 cur.bf = par.bf = 0 # 插入操作中, 操作的两个节点旋转后平衡因子恢复为0
右单旋转

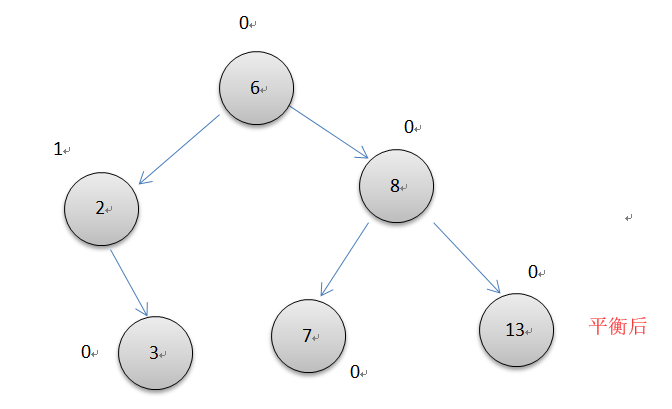
上图中插入3后左子树不平衡了,根节点8的平衡因子变为了-2, 此时应该以6为轴心向右单旋转一次,具体操作与左单旋转类似:8的左节点指向6的左节点(此时为7),6的右节点指向8,由于8原来是根节点,没有父节点,所以根节点指向6。旋转后6和8节点都恢复0的平衡因子了。代码如下,与左单循环基本一样。
def r_rotate(self, par, cur): """右单旋转""" p = cur.right cur.right = par par.left = p if p: p.parent = par if par == self.root: self.root = cur else: if par == par.parent.left: par.parent.left = cur else: par.parent.right = cur cur.parent = par.parent # 更新父节点信息 par.parent = cur cur.bf = par.bf = 0 # 更新平衡因子
左右双旋转
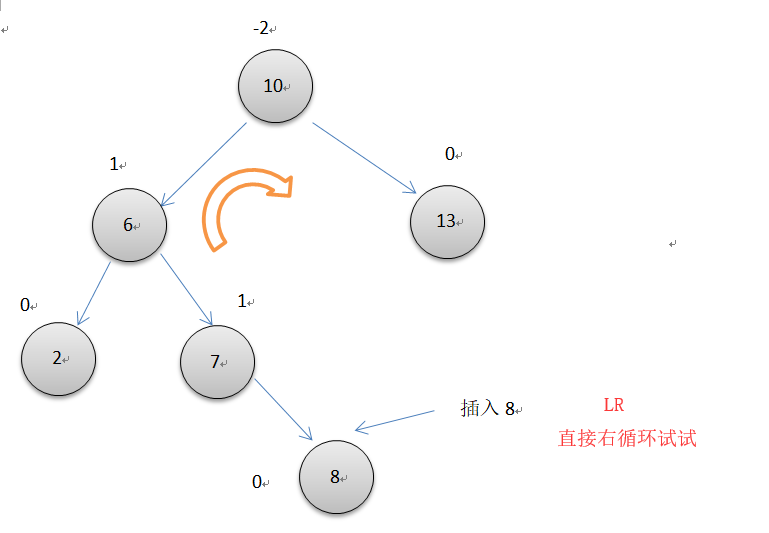
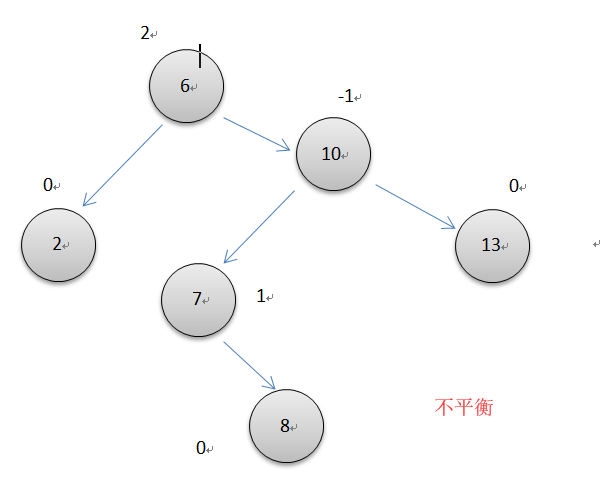
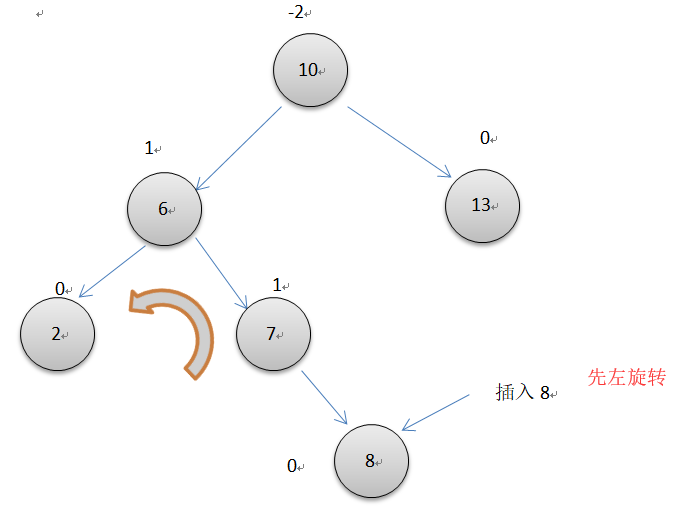

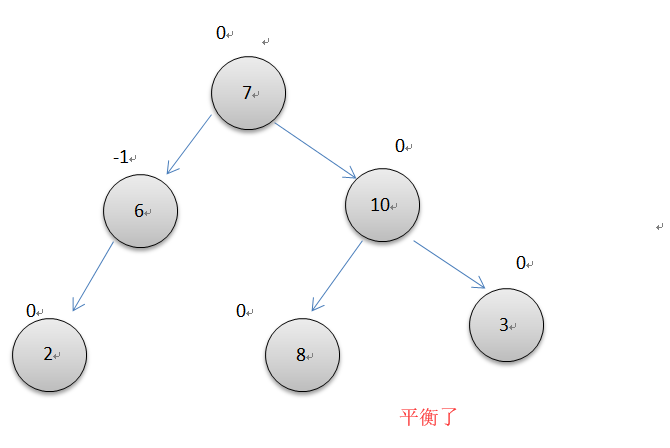
如上图所示,10节点的平衡因子为-2,而它的左节点的平衡因子却为1,两个节点失去平衡的方向不一样,所以要先以7位轴心对节点6左单旋转一次,再以7为轴心对节点10右旋转一次。操作细节和同上面单次循环一样。注意此时操作的3个节点的平衡因子要根据不同7的平衡因子单独调整。代码很简单,利用已经写好的左右单旋转即可完成。
def lr_rotate(self, par, cur): """左右双旋转""" # 先左旋转 cur 和 cur的右子节点 cur_right = cur.right # 获得cur的右子节点的引用 bf = cur_right.bf self.l_rotate(cur, cur_right) # 继续右旋转 self.r_rotate(par, cur_right) if bf == 0: # 根据cur_right的平衡因子更新操作的3个节点 cur.bf = cur_right.bf = par.bf = 0 elif bf == -1: par.bf = 1 cur.bf = cur_right.bf = 0 else: cur.bf = -1 cur_right.bf = par.bf = 0
右左双旋转
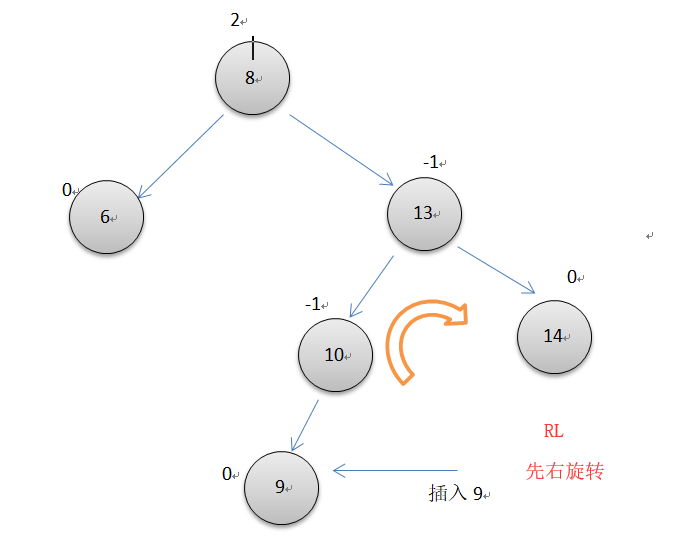

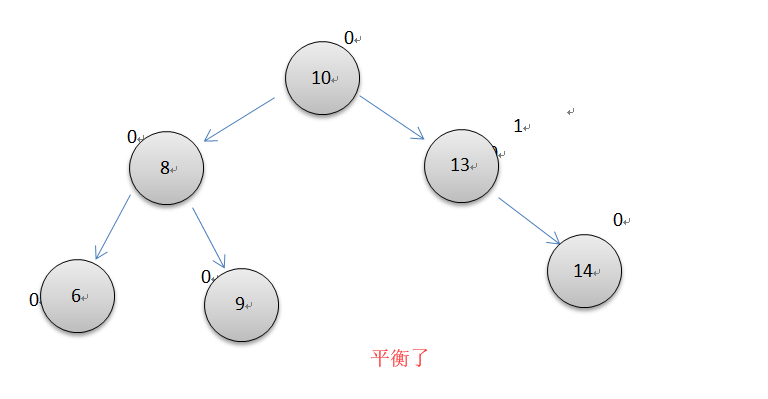
如上图所示,当一个节点的平衡因子为2,而它的右子节点的平衡因子为-1时,就需要先进行右旋转,再左旋转。注意中间节点13右旋转后的平衡因子变为1了。代码同左右双旋转类似。
def rl_rotate(self, par, cur): """右左双旋转""" # 先右旋转 cur 和 cur的左子节点 cur_left = cur.left # 获得cur的右子节点的引用 bf = cur_left.bf self.r_rotate(cur, cur_left) self.l_rotate(par, cur_left) # 继续右旋转 if bf == 0: # 根据cur_left的平衡因子更新操作的3个节点 cur.bf = cur_left.bf = par.bf = 0 elif bf == -1: cur.bf = 1 par.bf = cur_left.bf = 0 else: par.bf = -1 cur_left.bf = cur.bf = 0
平衡因子的更新
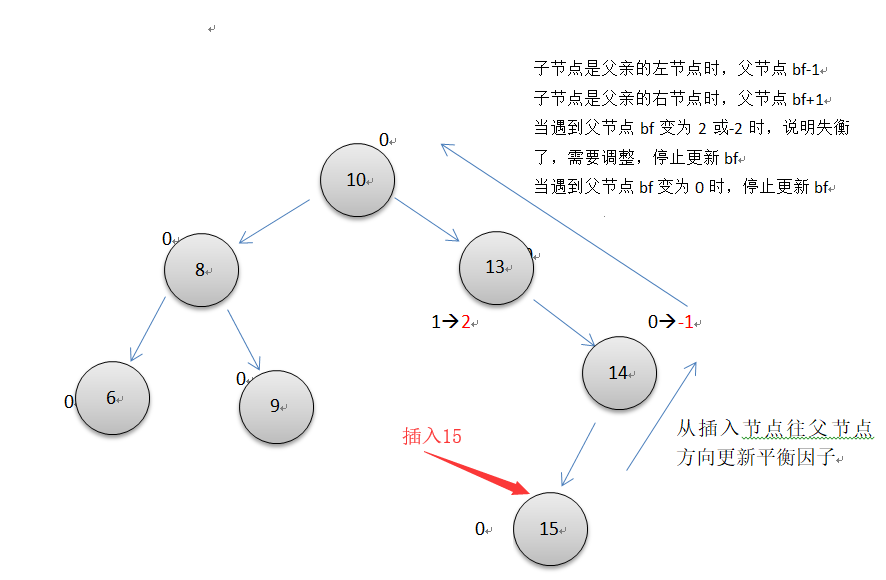
平衡因子的代码如下所示
def balance_by_insert(self, cur): """ 更新插入后的平衡因子, 平衡二叉树 :param cur: 当前插入节点cur :return: None """ par = cur.parent # 插入节点的父节点 while par: if cur == par.left: # 如果当前节点是父节点的左节点 par.bf -= 1 else: par.bf += 1 if par.bf == 0: # 为0说明没有增加树的高度, 返回 return if par.bf == -2: if cur.bf == 1: # 左右双向旋转 self.lr_rotate(par, cur) break else: self.r_rotate(par, cur) break elif par.bf == 2: if cur.bf == -1: # 右左双向旋转 self.rl_rotate(par, cur) break else: self.l_rotate(par, cur) break cur = par # 从添加的节点开始往上更新直到根节点 par = par.parent
查找
比起插入操作来说,查找就容易多了,从根节点开始遍历...代码如下
def find(self, key): """寻找键值""" p = self.root while p: if p.key == key: return p if key < p.key: p = p.left else: p = p.right return None
删除细节
删除操作也是一个难点,要考虑几种不同的情况
第一种情况
当要删除的节点直接是叶节点,那就直接删除
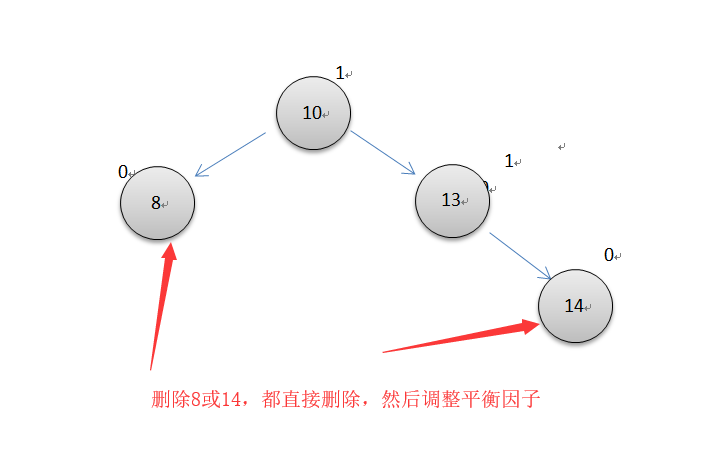
第二种情况
要删除的节点带有左子串或右子串
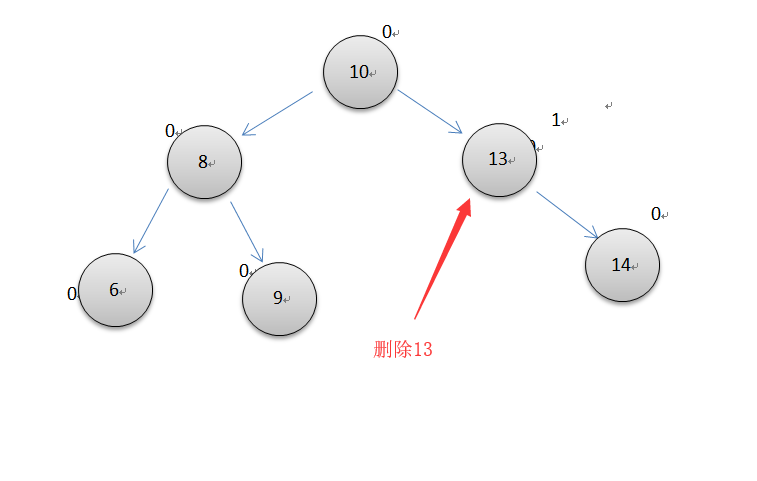
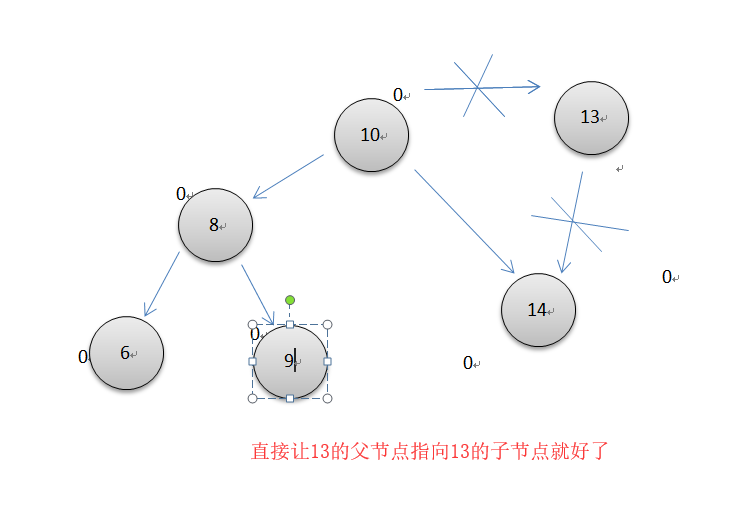
第三种情况
要删除的节点带有左子串和右子串

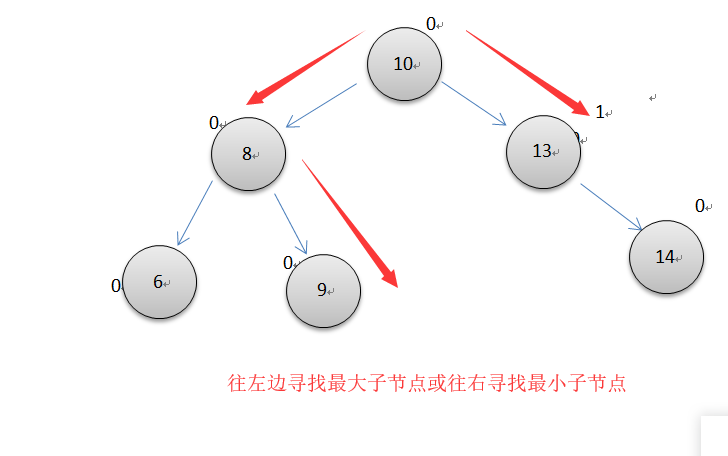
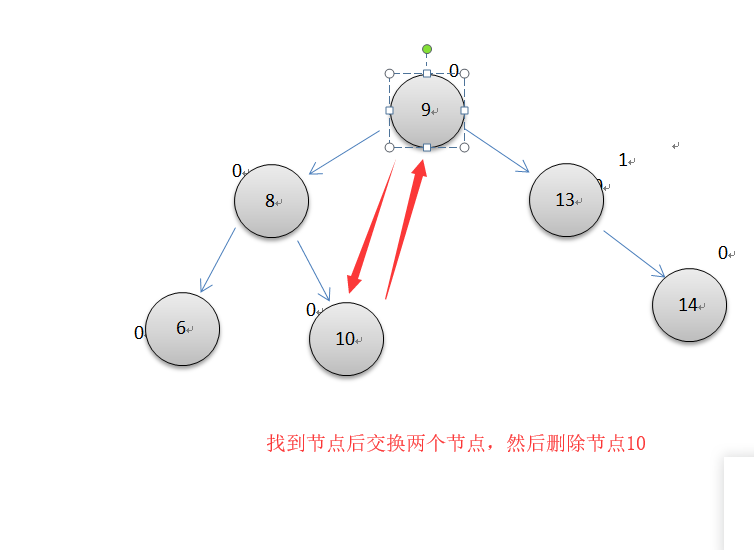
遇到第三种情况,就往左寻找最大子节点,或往右寻找最小子节点。找到交换完元素后,如上图所示,原来的节点9是叶节点,这就转换为情况一了,然后直接删除节点10,如果交换的节点原本就有子串,如上图,假设9有左子串,那么就相当于把情况转换为情况2了,变为删除一个带子节点的节点了。
删除的平衡因子更新
删除操作中,平衡因子的更新和插入操作类似,都是从删除节点的位置开始向父节点方向开始更新,更新时如果子节点是父节点的左节点,则父节点的bf+1,否则-1。直到根节点或原本平衡因子0的父节点因删除而变为1或为-1时才停下来。此时还要注意有一个关键与插入不同,当遇到一个节点不平衡时,旋转后可能还要继续往父节点处更新bf,只有两种特殊情况旋转后因为子节点高度没变,就不用往上更新了,下面有说明。
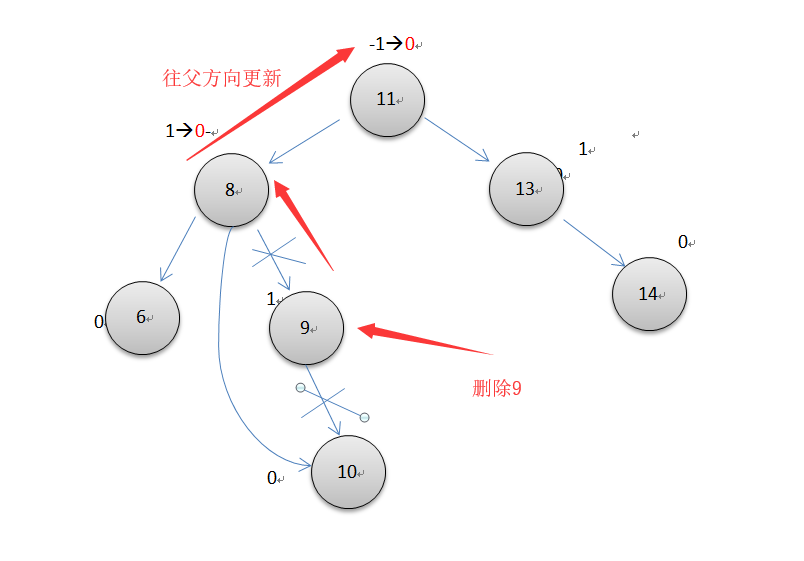
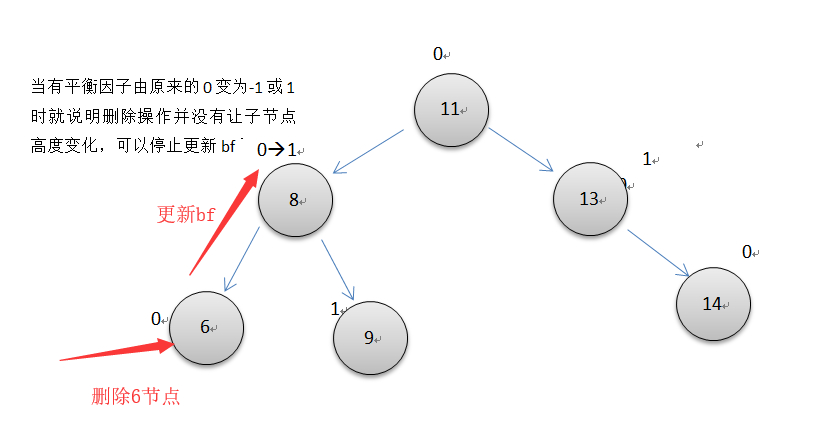
删除操作遇到不平衡的节点时也可以通过旋转恢复平衡,但旋转后可能需要继续往父节点更新平衡因子




当遇到下面两种情况时,参与左单旋转或右单旋转的两个节点的平衡因子并没有如插入操作一样恢复为0,但是因为这两种情况旋转后树的高度没变,所以可以停止往上更新平衡因子了。
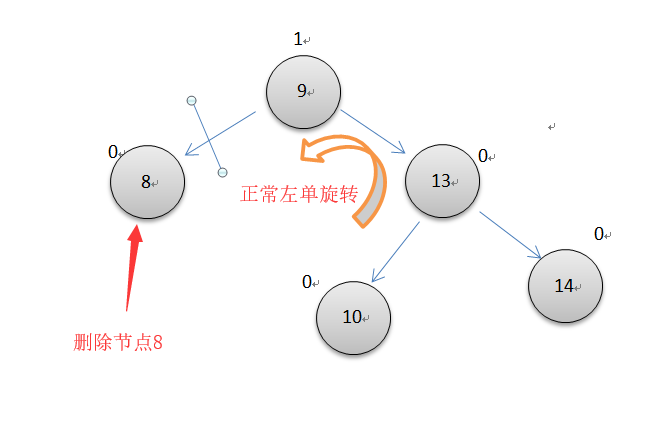


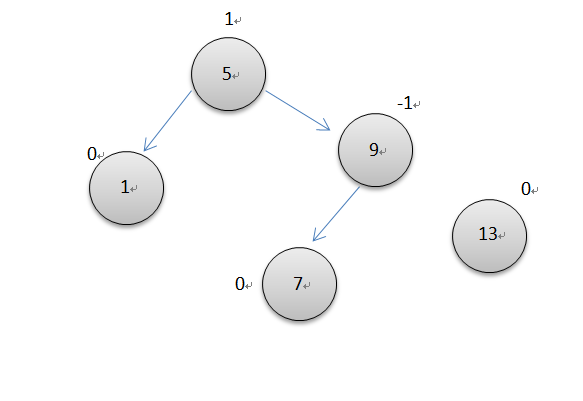
遇到上面两种情况单独处理就是了。以下是删除后的更新平衡因子的代码
def balance_by_delete(self, cur): """根据删除节点位置向上更新平衡因子""" par = cur.parent while par: if cur == par.left: # 如果当前节点是父节点的左节点 par.bf += 1 else: par.bf -= 1 if par.bf == 1 or par.bf == -1: # 为0说明没有增加树的高度, 返回 return if par.bf == -2: cur = cur.parent.left # 旋转是旋转与插入方向相反的两个节点 if cur.bf == 1: # 左右双向旋转 self.lr_rotate(par, cur) par = cur.parent # 更新一下par的指向 elif cur.bf == 0: self.r_rotate(par, cur) # 特殊情况树的高度并没有增加需要退出往上更新 cur.bf = 1 par.bf = -1 break else: self.r_rotate(par, cur) par = cur elif par.bf == 2: cur = cur.parent.right if cur.bf == -1: # 左右双向旋转 self.rl_rotate(par, cur) par = cur.parent # 更新一下par的指向 elif cur.bf == 0: self.l_rotate(par, cur) cur.bf = -1 par.bf = 1 break else: self.l_rotate(par, cur) par = cur cur = par # 从添加的节点开始往上更新直到根节点 par = par.parent
二叉树的图形化显示
1. 在线生成bst树和avl树
学习过程中难免遇到理解的问题: 图形化能很好的帮助我们理解问题,下面是两个在线生成二叉树的网址,根据自己需要看看,添加添加
2. 程序自己生成二叉树
利用PyGraphviz模块画出二叉树
参考网址:http://pygraphviz.github.io/documentation/pygraphviz-1.5/ 这里有详细的使用说明
安装该模块失败,参考这篇博客 https://blog.csdn.net/chirebingxue/article/details/50393755
我这次使用了该模块以完成最后生成的二叉树显示,代码如下
import pygraphviz as pgv def draw(self, filename='./tree.png'): g = pgv.AGraph(strict=False, directed=True) g.node_attr['shape'] = 'circle' def traver(node): if node: if not node.parent: g.add_node(node.key) else: g.add_edge(node.parent.key, node.key) traver(node.left) traver(node.right) traver(self.root) g.layout('dot') g.draw(filename)
简单的测试改模块的效果
tree = AVLTree() tree.insert(range(0, 20, 2)) # 自己简单实现了个可以接受一个可迭代对象的数值的插入 tree.draw() tree.delete_key(14) tree.draw('tree2.png')
最后生成下面的png图
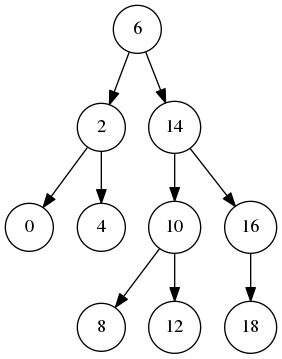

完整代码
最后附上个人的完整代码

1 """实现一个自平衡的AVLtree""" 2 from collections import deque, Iterable 3 import pygraphviz as pgv 4 import random 5 6 7 class Node(object): 8 def __init__(self, key, parent=None, left=None, right=None): 9 self.key = key # 存储的数据 10 self.parent = parent # 父节点 11 self.left = left # 左孩子节点 12 self.right = right # 右孩子节点 13 self.bf = 0 # 平衡因子 等于左子树高度减去右子树高度 14 15 16 class AVLTree(object): 17 def __init__(self, key=None): 18 if key: 19 self.root = Node(key) 20 else: 21 self.root = None 22 23 def insert(self, *keys): 24 """插入键值,键可以是个可迭代对象,或是多个独立的键""" 25 if isinstance(keys[0], Iterable): 26 if len(keys) > 1: 27 print("插入失败...第一个参数可迭代对象时参数只能有一个") 28 return 29 keys = keys[0] 30 else: 31 keys = keys 32 for key in keys: 33 if not self.root: 34 self.root = Node(key) 35 else: 36 p = self.root 37 while 1: 38 if key == p.key: 39 print("%d键已存在, 跳过该键" % key) 40 break 41 elif key < p.key: 42 if not p.left: # 当前左节点可以添加 43 cur_node = Node(key, p) 44 p.left = cur_node 45 self.balance_by_insert(cur_node) 46 break 47 else: 48 p = p.left 49 else: 50 if not p.right: 51 cur_node = Node(key, p) 52 p.right = cur_node 53 self.balance_by_insert(cur_node) 54 break 55 else: 56 p = p.right 57 58 def balance_by_insert(self, cur): 59 """ 60 更新插入后的平衡因子, 平衡二叉树 61 :param cur: 当前插入节点cur 62 :return: None 63 """ 64 par = cur.parent # 插入节点的父节点 65 while par: 66 if cur == par.left: # 如果当前节点是父节点的左节点 67 par.bf -= 1 68 else: 69 par.bf += 1 70 if par.bf == 0: # 为0说明没有增加树的高度, 返回 71 return 72 if par.bf == -2: 73 if cur.bf == 1: # 左右双向旋转 74 self.lr_rotate(par, cur) 75 break 76 else: 77 self.r_rotate(par, cur) 78 break 79 elif par.bf == 2: 80 if cur.bf == -1: # 左右双向旋转 81 self.rl_rotate(par, cur) 82 break 83 else: 84 self.l_rotate(par, cur) 85 break 86 cur = par # 从添加的节点开始往上更新直到根节点 87 par = par.parent 88 89 def balance_by_delete(self, cur): 90 """根据删除节点位置向上更新平衡因子""" 91 par = cur.parent 92 while par: 93 if cur == par.left: # 如果当前节点是父节点的左节点 94 par.bf += 1 95 else: 96 par.bf -= 1 97 if par.bf == 1 or par.bf == -1: # 为0说明没有增加树的高度, 返回 98 return 99 if par.bf == -2: 100 cur = cur.parent.left # 旋转是旋转与插入方向相反的两个节点 101 if cur.bf == 1: # 左右双向旋转 102 self.lr_rotate(par, cur) 103 par = cur.parent # 更新一下par的指向 104 elif cur.bf == 0: 105 self.r_rotate(par, cur) # 特殊情况树的高度并没有增加需要退出往上更新 106 cur.bf = 1 107 par.bf = -1 108 break 109 else: 110 self.r_rotate(par, cur) 111 par = cur 112 elif par.bf == 2: 113 cur = cur.parent.right 114 if cur.bf == -1: # 左右双向旋转 115 self.rl_rotate(par, cur) 116 par = cur.parent # 更新一下par的指向 117 elif cur.bf == 0: 118 self.l_rotate(par, cur) 119 cur.bf = -1 120 par.bf = 1 121 break 122 else: 123 self.l_rotate(par, cur) 124 par = cur 125 cur = par # 从添加的节点开始往上更新直到根节点 126 par = par.parent 127 128 def delete_key(self, key): 129 """删除键值, 通过三个子函数实现功能处理三种情况""" 130 131 def first(node): 132 """第一种情况, 找到的键本身是叶节点, 直接删除""" 133 self.balance_by_delete(node) 134 if node == node.parent.left: 135 node.parent.left = None 136 else: 137 node.parent.right = None 138 del node 139 140 def second(node): 141 """第二种, 找到的键本身带有左子节点或右子节点""" 142 par = node.parent # 获得该键的父节点引用 143 if node.left: # 该节点只有左节点 144 if par is None: # 说明该节点是root 145 self.root = node.left 146 node.left.parent = None 147 elif node == par.left: # 该节点是父节点的左节点 148 par.left = node.left 149 node.left.parent = par 150 else: 151 par.right = node.left 152 node.left.parent = par 153 self.balance_by_delete(node.left) 154 else: 155 if par is None: 156 self.root = node.right 157 node.left.parent = None 158 elif node == par.left: 159 par.left = node.right 160 node.right.parent = par 161 else: 162 par.right = node.right 163 node.right.parent = par 164 self.balance_by_delete(node.right) 165 del node 166 167 def third(node): 168 p = node.left # 寻找左边最大的子节点代替 169 while p.right: 170 p = p.right # 寻找最大子节点 171 172 node.key, p.key = p.key, node.key # 交换两个节点,这里的交换取了个巧,只交换值就不用处理节点之间的复杂关系了 173 if p.left or p.right: # 转换为第二种或第一种情况 174 second(p) 175 else: 176 first(p) 177 178 cur = self.find(key) # 寻找要删除的值 179 if cur: 180 if cur.left and cur.right: 181 third(cur) 182 elif not cur.left and not cur.right: # 直接是叶节点, 第一种情况 183 first(cur) 184 else: # 第二种情况, 只有左节点或右节点 185 second(cur) 186 else: 187 print("键值不存在, 删除失败") 188 189 def find(self, key): 190 """寻找键值""" 191 p = self.root 192 while p: 193 if p.key == key: 194 return p 195 if key < p.key: 196 p = p.left 197 else: 198 p = p.right 199 return None 200 201 def r_rotate(self, par, cur): 202 """右单旋转""" 203 p = cur.right 204 cur.right = par 205 par.left = p 206 if p: 207 p.parent = par 208 if par == self.root: 209 self.root = cur 210 else: 211 if par == par.parent.left: 212 par.parent.left = cur 213 else: 214 par.parent.right = cur 215 216 cur.parent = par.parent # 更新父节点信息 217 par.parent = cur 218 cur.bf = par.bf = 0 # 更新平衡因子 219 220 def l_rotate(self, par, cur): 221 """ 222 左单旋转 223 :param par: 平衡因子为2|-2的节点 224 :param cur: 作为轴心旋转的节点(平衡因子不为2) 225 :return: None 226 """ 227 p = cur.left # 辅助引用p指向cur的左节点 228 cur.left = par # cur的左节点指向par 229 par.right = p # par的右节点指向cur的左节点 230 if p: 231 p.parent = par # cur的左节点不为空时更新该节点的父节点 232 if par == self.root: 233 self.root = cur # 判断平衡因子为2的par是否为根 234 else: 235 if par == par.parent.left: # 更新par父节点的子节点信息 236 par.parent.left = cur 237 else: 238 par.parent.right = cur 239 cur.parent = par.parent # 当前cur的父节点指向原来par的父节点 240 par.parent = cur # par变为cur的左子节点 241 242 cur.bf = par.bf = 0 # 插入操作中, 操作的两个节点旋转后平衡因子恢复为0 243 244 def lr_rotate(self, par, cur): 245 """左右双旋转""" 246 # 先左旋转 cur 和 cur的右子节点 247 cur_right = cur.right # 获得cur的右子节点的引用 248 bf = cur_right.bf 249 self.l_rotate(cur, cur_right) 250 # 继续右旋转 251 self.r_rotate(par, cur_right) 252 if bf == 0: # 根据cur_right的平衡因子更新操作的3个节点 253 cur.bf = cur_right.bf = par.bf = 0 254 elif bf == -1: 255 par.bf = 1 256 cur.bf = cur_right.bf = 0 257 else: 258 cur.bf = -1 259 cur_right.bf = par.bf = 0 260 261 def rl_rotate(self, par, cur): 262 """右左双旋转""" 263 # 先右旋转 cur 和 cur的左子节点 264 cur_left = cur.left # 获得cur的右子节点的引用 265 bf = cur_left.bf 266 self.r_rotate(cur, cur_left) 267 self.l_rotate(par, cur_left) # 继续右旋转 268 if bf == 0: # 根据cur_left的平衡因子更新操作的3个节点 269 cur.bf = cur_left.bf = par.bf = 0 270 elif bf == -1: 271 cur.bf = 1 272 par.bf = cur_left.bf = 0 273 else: 274 par.bf = -1 275 cur_left.bf = cur.bf = 0 276 277 def get_tree_state(self, _tree=None): 278 """返回树的高度和元素数量和树是否平衡组成的一个元祖""" 279 if not _tree: 280 _tree = self.root 281 count = 0 282 is_balanced = True 283 284 def get_state(_tree): 285 nonlocal count, is_balanced 286 if not _tree: 287 return 0 288 count += 1 289 h1 = get_state(_tree.left) + 1 290 h2 = get_state(_tree.right) + 1 291 if abs(h1 - h2) >= 2: 292 is_balanced = False 293 return max((h1, h2)) 294 return get_state(_tree), count, is_balanced 295 296 def pre_traversal(self): 297 """先序遍历""" 298 def traver(node): 299 if node: 300 print(node.key, end=' ') 301 traver(node.left) 302 traver(node.right) 303 304 traver(self.root) 305 print() 306 307 def in_order_traversal(self): 308 """中序遍历""" 309 _node = self.root 310 311 def traver(node): 312 if node: 313 traver(node.left) 314 print(node.key, end=' ') 315 traver(node.right) 316 317 traver(_node) 318 print() 319 320 def level_traversal(self): 321 """层次遍历, 自己简单把树分层打印出来""" 322 d = deque() 323 d.append((1, 1, self.root)) # 元祖表示第1层第1个数 324 level = 2 325 level_count = 0 # 每层的数量 326 last_l = 1 327 while d: 328 # p = d.popleft() 329 ll, c, p = d.popleft() 330 if ll != last_l: 331 last_l = ll 332 print("") 333 # print(p.key, 'bf: %s' % p.bf, end=' ') 334 print(p.key, end=' ') 335 level_count += 1 336 if p.left: 337 d.append((level, level_count, p.left)) 338 339 level_count += 1 340 if p.right: 341 d.append((level, level_count, p.right)) 342 if level_count == pow(2, level-1): 343 level_count = 0 344 level += 1 345 print() 346 347 def draw(self, filename='./tree.png'): 348 """生成二叉树的图片文件""" 349 g = pgv.AGraph(strict=False, directed=True) 350 g.node_attr['shape'] = 'circle' 351 352 def traver(node): 353 if node: 354 if not node.parent: 355 g.add_node(node.key) 356 else: 357 g.add_edge(node.parent.key, node.key) 358 traver(node.left) 359 traver(node.right) 360 traver(self.root) 361 g.layout('dot') 362 g.draw(filename)
测试代码:
1 from AVL_Tree import AVLTree 2 import random 3 import os 4 5 path = './tree_pic' 6 if not os.path.exists(path): 7 os.mkdir(path) 8 9 # 创建一个生成器, 做图片的名称 10 g = (path + '/tree' + str(i) + '.png' for i in range(1, 30)) 11 12 t = AVLTree() 13 # lst = [random.randrange(20, 300) for i in range(20)] 14 lst = random.sample(range(30, 300), 20) 15 t.insert(lst) 16 print(lst) 17 t.draw(next(g)) 18 print(t.get_tree_state()) 19 for i in range(8): 20 k = random.choice(lst) 21 print("删除键%d" % k) 22 t.delete_key(k) 23 print(t.get_tree_state()) # 打印树的高度, 元素个数,树是否平衡 24 t.draw(next(g)) 25 26 27 t.insert(-5, 200, 300) 28 t.insert(10, 0, 410, 15, 500) 29 t.draw(next(g)) 30 print(t.get_tree_state())
控制台输出

[100, 89, 217, 202, 206, 98, 187, 34, 293, 162, 292, 236, 279, 37, 269, 80, 237, 52, 222, 155] (5, 20, True) 删除键217 (5, 19, True) 删除键155 (5, 18, True) 删除键217 键值不存在, 删除失败 (5, 18, True) 删除键293 (5, 17, True) 删除键98 (5, 16, True) 删除键98 键值不存在, 删除失败 (5, 16, True) 删除键52 (5, 15, True) 删除键292 (5, 14, True) (6, 22, True)
生成的二叉树的前两张和最后一张图片

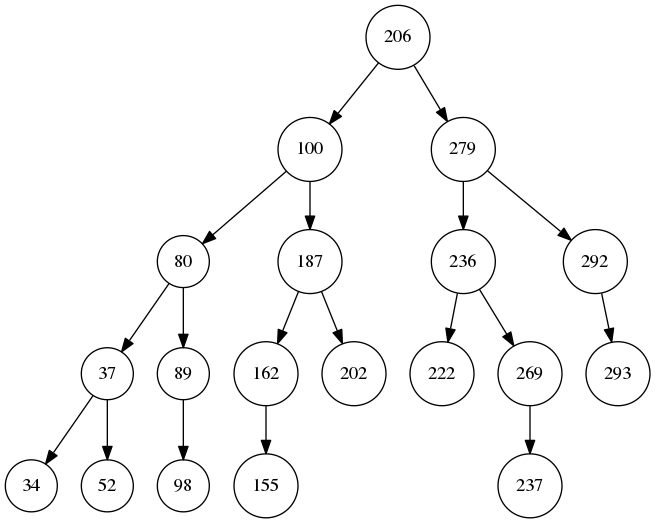
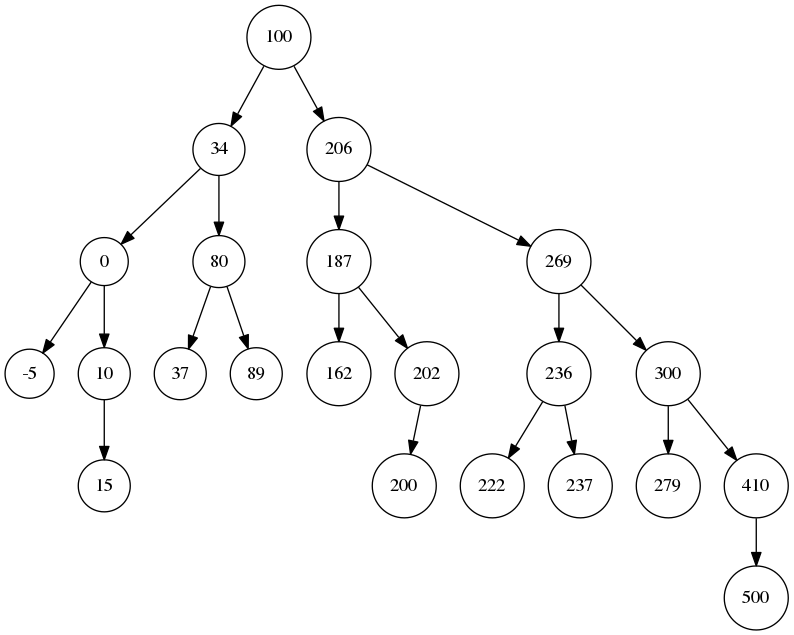
参考:
感谢他们的博客
- https://blog.csdn.net/qq_37941471/article/details/79706523
- https://www.cnblogs.com/fullsail/p/3729015.html?utm_source=tuicool
- http://www.cnblogs.com/skywang12345/p/3577479.html



