经典算法详解（10）图中有多少个三角形

题目：请说出下面图形中包含多少个三角形？请用一个程序完成计算。

C++版本

 1 #include<iostream>
 2 
 3 using namespace std;
 4 
 5 const char NO_POINT = '0';
 6 
 7 //任意的一条线
 8 const char *map[] = { "ad","ab","db","ae","aj","ah","ej","eh","jh","af","ak","ai","fk","fi","ki","ag","ac","gc",
 9 "de","df","dg","ef","eg","fg","bj","bk","bg","jk","jg","kg","bh","bi","bc","hi","hc","ic" };
10 //共线的点
11 const char *line[] = { "adb","aejh","afki","agc","defg","bjkg","bhic" };
12 
13 //点是否在线上
14 int contain( const char *str, char a) {
15     int i = 0;
16     while (str[i] != '\0') {        //注意字符使用单引号，字符串是双引号
17         if (str[i] == a)
18             return 1;
19         i++;
20     }
21     return 0;
22 }
23 
24 //三个点是否在一条线上函数
25 int isInALine(const char *str[], char a, char b, char c) {
26     int i ;
27     for (i = 0; i < 7; i++) {
28         if (contain(str[i], a) && contain(str[i], b) && contain(str[i], c)) {
29             return 1;
30         }
31     }
32     return 0;
33 }
34 
35 //两条线的交点函数
36 char getCrossPoint(const char *str1, const char *str2) {
37     if (*str1 == *str2)
38         return *str1;
39     if (*str1 == *(str2 + 1))
40         return *str1;
41     if (*(str1 + 1) == *str2)
42         return *(str1 + 1);
43     if (*(str1 + 1) == *(str2 + 1))
44         return *(str1 + 1);
45     return NO_POINT;
46 }
47 
48 //三条线两两必须有交点，并且三条线不能共线才能构成三角形。
49 int isTriangle(const char *str1, const char *str2, const char *str3) {
50     char Point1, Point2, Point3;
51     Point1 = getCrossPoint(str1, str2);
52     if (Point1 == NO_POINT)
53         return 0;
54     Point2 = getCrossPoint(str1, str3);
55     if (Point2 == NO_POINT)
56         return 0;
57     Point3 = getCrossPoint(str2, str3);
58     if (Point3 == NO_POINT)
59         return 0;
60     if (isInALine(line, Point1, Point2, Point3))
61         return 0;
62     return 1;
63 }
64 
65 int getTriangelCount( const char *str[]) {
66     int i, j, k,count=0;
67     for (i = 0; i < 36; i++) {
68         for (j = i+1; j < 36; j++) {
69             for (k = j+1; k < 36; k++) {
70                 if (isTriangle(str[i], str[j], str[k]))
71                     count++;
72             }
73         }
74     }
75     return count;
76 }
77 
78 int main(int argc, char *argv[]) {
79     cout << getTriangelCount(map);
80     getchar();
81     return 0;
82 }

 解题思路：

（1）给每个交点做标记，如下：

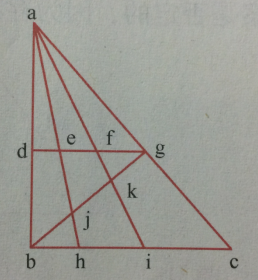
（2）总共有36条线段，如果三条线段两两之间存在交点，但一条线上（已经包含了三条线交于同一点），则可以构成三角形。如下图所示，最左边的构成三角形，右边两个不构成三角形：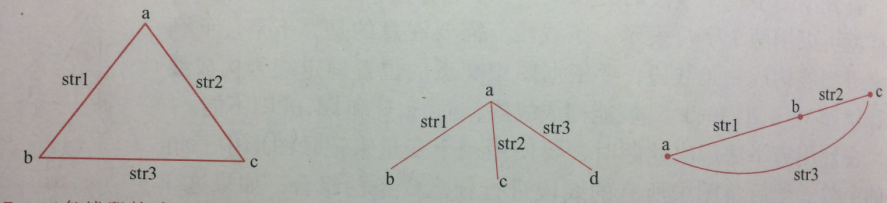

（3）故需要有如下一些子函数：求两条线的交点，三个点是否共线等。

posted @ 2018-07-15 18:52  ysyouaremyall  阅读(8473)  评论(0)  编辑  收藏  举报