吴恩达《机器学习》课程总结(4)多变量线性回归
4.1多维特征
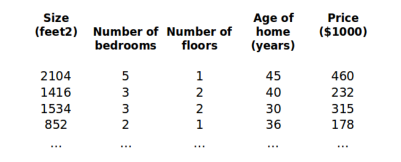
上图中列数即为特征的个数,行数是样本数。函数假设如下:
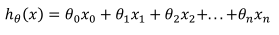
其中x0=1。
4.2多变量梯度下降
和单变量的损失函数相同:
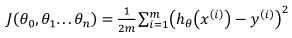
其中,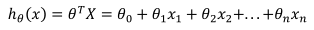
求导迭代如下:

4.3梯度下降法实践1-特征缩放
特征之间的尺度变化相差很大(如一个是0-1000,一个是0-5),梯度算法需要非常多次的迭代才能收敛,如下图所示:
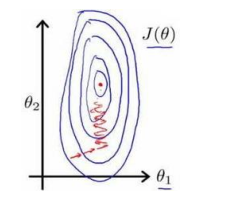
方法:将各个特征缩放至大致相同的尺度,最简单的方法就是特征减去均值除以方差。如下所示:
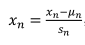
4.4梯度下降法实践2-学习率
学习率过小收敛慢,学习率过大可能导致无法收敛。
通常通过三倍放大来考虑学习率的设置,比如:0.01,0.03,0.1,0.3,1,3,10……。
4.5特征和多项式回归
比如一个二次模型:
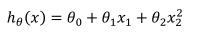
或者三次模型:
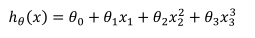
可以通过创建新特征(即令):
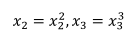
从而将模型转换成线性模型。
4.6正规方程
前提:对于某些线性回归问题,使用正规方程求解一步到位(导数为零等式求解)。如下所示

直接令
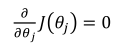 。
。
参数的解直接为:
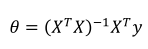
(X包含x0=1)。
梯度下降与正规方程的比较:
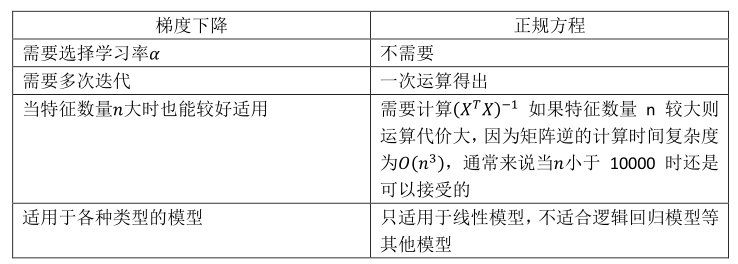
4.7正规方程及不可逆性:
(1)特征之间互相不独立时不可逆;
(2)样本数少于特征数时不可逆。

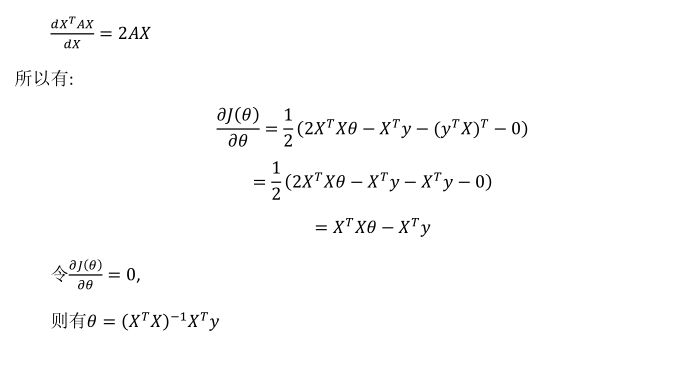



 浙公网安备 33010602011771号
浙公网安备 33010602011771号