P2486 [SDOI2011]染色
题目链接：https://www.luogu.com.cn/problem/P2486
题是好题，毒也很毒。
一杯酒，一键盘，一份代码敲一天，缝缝补补又几年；
最后喜得中国红；
本题质量还是非常上乘的。
一，仔细理解题意；
注意到他是求一段区间内有多少个颜色段，并不是求一段区间内有多少种颜色。一开始因为这个十分疑惑该怎么用线段树进行维护。
二，如何维护区间内多少段颜色段。
考虑到线段树，对于区间更改颜色，这个很简单了。那我们如何把两个子区间合并成一个大区间呢?
假设一段连续的区间值为：123345,首先定义sum[l-r]表示区间[l,r]有多少个颜色段；那么
sum[1-6]=sum[1-3] + sum[4-6];然后注意到有可能3跟4是一种颜色，我们可以通过在维护每个区间的左右端点颜色，进行判断。
如果3-4是一种颜色，那么sum[1-6]就要减1.
所以代码为：
sum[id] = sum[id * 2] + sum[id * 2 + 1];
if(R_color[id * 2] == L_color[id * 2 + 1]) sum[id] --;
我们通过树链剖分可以轻松的对每个区间进行维护，树链剖分就不细讲了。
我们继续考虑一种情况。
上为样例的一个微改图；
如果我们此时查询编号为5和3结点之间有多少个不同的颜色段。
首先他的重链是1-2-4这条链，用紫色表明了。
所以在查询的时候，我会先查询4-4（注意查询区间是dfs序，不是编号）这个区间,发现1个颜色段。
在去查询6-6这个区间，发现1个颜色段。
最后查询（1-2）这个区间发现一个颜色段。
我们把他加起来为3个颜色段，但是根据图而言是只有一个颜色段的。
产生差异的主要原因，在于他当前结点fx区间[l-r]有可能会跟结点fx的父亲区间相同颜色，从而产生差异。
所以，我们在写的时候，需要把他这条链上最顶上（也就是区间的l值位置）的颜色用ans1记录下来并与他父亲的那个区间的右端点进行比较。如果相同，则要减一。
同样，因为另外一个结点做相同考虑，用ans2记录下来。
最后还有一种情况，需要考虑仔细：
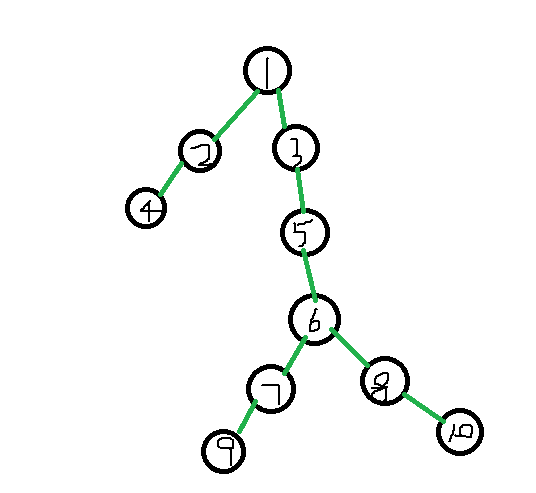
如果我们考虑结点编号为4，10之间的颜色段，一定要注意ans1和ans2的维护。
因为这个维护错了不知道多少次。
#include"stdio.h"
#include"string.h"
#include"algorithm"
using namespace std;
inline int read(){
int f = 1, x = 0;char ch = getchar();
while (ch > '9' || ch < '0'){if (ch == '-')f = -f;ch = getchar();}
while (ch >= '0' && ch <= '9'){x = x * 10 + ch - '0';ch = getchar();}
return x * f;
}
const int N = 200010;
int n,q,root,mod,m;
int head[N],ver[N],Next[N],tot;///树的结构存储
int val[N];///存储每个结点的信息
int d[N],son[N],far[N],Size[N];///结点的深度，重儿子，祖先
int a[N],sum[N * 4];///线段树上的结点值，maxx,sum值
int L_color[N * 4],R_color[N * 4];///一个区间最左最右边的颜色
int dfn[N],top[N],id[N];///存储dfs序，top是条链的祖先，id是每个结点在dfn中序列的下标位置
int cnt;///表示的是dfs序列的最后一个位置
int laze[N * 4],now[N * 4];
void add(int x,int y){ ///添加树边
ver[++ tot] = y; Next[tot] = head[x]; head[x] = tot;
}
void Build_Tree(int id,int l,int r)
{
laze[id] = now[id] = 0;
L_color[id] = R_color[id] = 0;
if(l == r)
{
laze[id] = 0; now[id] = 0;
L_color[id] = R_color[id] = val[dfn[l]];
sum[id] = 1; return ;
}
int mid = (l + r) >> 1;
Build_Tree(id * 2,l,mid);
Build_Tree(id * 2 + 1,mid + 1,r);
sum[id] = sum[id * 2] + sum[id * 2 + 1];
L_color[id] = L_color[id * 2]; R_color[id] = R_color[id * 2 + 1];
if(R_color[id * 2] == L_color[id * 2 + 1]) sum[id] --;
return ;
}
void spread(int id,int l,int r)
{
int mid = (l + r) >> 1;
if(laze[id])
{
sum[id * 2] = 1;
sum[id * 2 + 1] = 1;
laze[id * 2] = 1; now[id * 2] = now[id];
laze[id * 2 + 1] = 1; now[id * 2 + 1] = now[id];
L_color[id * 2] = R_color[id * 2] = now[id];
L_color[id * 2 + 1] = R_color[id * 2 + 1] = now[id];
laze[id] = 0; now[id] = 0;
}
return ;
}
void Update(int id,int L,int R,int l,int r,int x)///将loc上的值进行更新
{
if(l <= L && r >= R)
{
laze[id] = 1; now[id] = x;
sum[id] = 1; L_color[id] = R_color[id] = x;
return ;
}
spread(id,L,R);
int mid = (L + R) >> 1;
if(l <= mid) Update(id * 2,L,mid,l,r,x);
if(r > mid) Update(id * 2 + 1,mid + 1,R,l,r,x);
sum[id] = sum[id * 2] + sum[id * 2 + 1];
if(R_color[id * 2] == L_color[id * 2 + 1]) sum[id] --;
L_color[id] = L_color[id * 2]; R_color[id] = R_color[id * 2 + 1];
return ;
}
int now_L = 0,now_R = 0;
int Query_sum(int id,int L,int R,int l,int r)///查询[l,r]区间和
{
if(L > r || R < l) return 0;
if(l <= L && r >= R)
{
if(l == L)
now_L = L_color[id];
if(r == R)
now_R = R_color[id];
return sum[id];
}
spread(id,L,R);
int mid = (L + R) >> 1;
int ans = Query_sum(id * 2,L,mid,l,r)+ Query_sum(id * 2 + 1,mid + 1,R,l,r);
if(l <= mid && r > mid)
{
if(R_color[id * 2] == L_color[id * 2 + 1])
ans --;
}
sum[id] = sum[id * 2] + sum[id * 2 + 1];
if(R_color[id * 2] == L_color[id * 2 + 1]) sum[id] --;
L_color[id] = L_color[id * 2]; R_color[id] = R_color[id * 2 + 1];
return ans;
}
void dfs1(int u,int f,int dep)///dfs1指在处理d数组，son数组，far数组,Size数组
{
d[u] = dep; far[u] = f;
Size[u] = 1; son[u] = -1;
for(int i = head[u]; i; i = Next[i]){
int v = ver[i];
if(v == f) continue;
dfs1(v,u,dep+1);
Size[u] += Size[v];
if(son[u] == -1 || Size[son[u]] < Size[v])
son[u] = v;
}
}
void dfs2(int u,int T)///旨在处理重链，和dfs序列
{
dfn[++ cnt] = u;id[u] = cnt;
top[u] = T;
if(son[u] == -1) return ;
dfs2(son[u],T);
for(int i = head[u]; i; i = Next[i]){
int v = ver[i];
if(v != son[u] && v != far[u]){
dfs2(v,v);
}
}
}
int main()
{
n = read(); m = read();
for(int i = 1; i <= n; i ++)
val[i] = read();
for(int i = 1; i < n; i ++)
{
int x,y; scanf("%d%d",&x,&y);
add(x,y); add(y,x);
}
q = m;
cnt = 0; root = 1;
dfs1(root,root,1);
dfs2(root,root);
Build_Tree(1,1,n);
while(q --)
{
int op;char str[15]; scanf("%s",str);
if(str[0] == 'C') op = 1; else op = 0;
if(op == 1)
{
int x,y,c; scanf("%d%d%d",&x,&y,&c);
int fx = top[x]; int fy = top[y];
while(fx != fy)
{
if(d[fx] > d[fy])
{
Update(1,1,n,id[fx],id[x],c);
x = far[fx]; fx = top[x];
}
else {
Update(1,1,n,id[fy],id[y],c);
y = far[fy]; fy = top[y];
}
}
if(id[x] <= id[y])
Update(1,1,n,id[x],id[y],c);
else Update(1,1,n,id[y],id[x],c);
} else {
now_L = 0,now_R = 0;
int ans1 = 0,ans2 = 0;
int x,y; scanf("%d%d",&x,&y);
int fx = top[x],fy = top[y];
int ans = 0;int ttt = 0;
while(fx != fy)
{
if(d[fx] > d[fy])
{
ttt = Query_sum(1,1,n,id[fx],id[x]);
ans += ttt;
x = far[fx]; fx = top[x];
if(now_R == ans1) ans --;
ans1 = now_L;
} else
{
ttt = Query_sum(1,1,n,id[fy],id[y]);
ans += ttt;
y = far[fy]; fy = top[y];
if(now_R == ans2) ans --;
ans2 = now_L;
}
}
if(d[x] < d[y])
{
ttt = Query_sum(1,1,n,id[x],id[y]); ans += ttt;
if(now_L == ans1) ans --; if(now_R == ans2) ans --;
}
else {
ttt = Query_sum(1,1,n,id[y],id[x]); ans += ttt;
if(now_R == ans1) ans --; if(now_L == ans2) ans --;
}
printf("%d\n",ans);
}
}
}
