Deeplab学习笔记
http://www.2cto.com/kf/201605/512286.html
无向图
无向图就是指边没有方向的图,这个图是有节点和连接节点的边组成的集合,像下面这样:
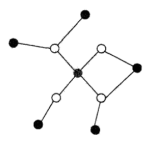
一组随机变量Y={Y1,Y2,...,Yn}, 具有联合概率分布P(Y),无向图中的节点表示一个个随机变量,边表示随机变量之间的依赖关系。节点和边分别记作v和e,节点和边的集合分别记作V和E,于是无向图就记作G=(V, E)。
马尔可夫随机场(MRF)
成对马尔可夫性:
无向图G=(V,E)中假设有两个不连接的节点u和v,其分别对应随机变量Yu和Yv,剩余的节点记为O,对应随机变量为YO。u和v满足成对马尔科夫性的条件是:(局部马尔科夫性和全局马尔科夫性与成对马尔科夫性等价)
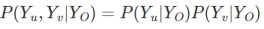
即在给定YO的情况下,Yu与Yv是独立的。
如果无向图G=(V,E)的任意两个节点均满足成对马尔科夫性,则G是一个马尔科夫随机场。
条件随机场(CRF)
X,Y是随机变量,分别代表输入和输出,P(Y|X)是在给定X的条件下Y的条件概率分布。若在给定输入X的情况下,随机变量Y构成的无向图G=(V,E)是一个马尔科夫随机场,那么P(Y|X)为条件随机场。
马尔科夫随机场与条件随机场的比较
MRF关注联合概率分布,CRF关注条件概率分布。所以MRF属于生成模型,而CRF属于判别模型。生成模型本身比判别模型描述能力强,因为联合概率分布可以推导出条件概率分布:
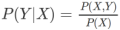
线性链条件随机场
设X = (X1, X2,..., Xn), Y = (Y1, Y2, ..., Yn)均为线性链表示的随机变量序列,若在给定随机变量序列X的条件下,随机变量序列Y的条件概率分布P(Y|X)构成条件随机场,即满足马尔可夫性:
P(Yi| X, Y1, ..., Yi-1, Yi+1, ...., Yn)= P(Yi | X, Yi-1, Yi+1)
i= 1, 2, ..., n (在i=1和n时只考虑单边)
则称P(Y|X)为线性链条件随机场。
上面的等式意思就是说Yi的概率只与Yi前后连接的Yi-1和Yi+1有关,示意图如下:

定义:线性链条件随机场的参数化形式
设P(Y|X)为线性链条件随机场,则在随机变量X取值为x(x表示的是一个观察序列)的条件下,随机变量Y取值为y(y表示的是一个标注序列)的条件概率具有如下形式:
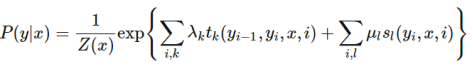
其中,
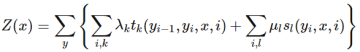
式中,tk和sl是特征函数,特征函数tk和sl取值为1或0;当满足特征条件时取值为1,否则为0,λk和μl是对应的权值,k代表的是第k个转移特征函数,l表示的是第l个状态特征函数,i表示的是序列y中第i个节点。Z(x)是规范化因子,相当于是把条件概率归一化,求和是在所有可能的标注序列y上进行的。
t(yi-1, yi, x, i)表达“在给定观测x,从上个节点i-1标记为yi-1转移到节点i标记为yi的情况”
s(yi, x, i)表达“当前节点i标记为yi的情况”
实际应用的例子:
http://www.jianshu.com/p/55755fc649b1
词性标注问题(就是给一个句子中的每个单词注明词性),例如:
“Bob drank coffee at Starbucks”这个句子序列标注后的词性序列为:(名词,动词,名词,介词,名词)
句子序列是观察序列,标注的词性序列是标注序列
x 表示的是我们要标注词性的句子
i 用来表示句子x中第i个单词
yi-1 给第i-1个单词标注的词性
yi 给第i个单词标注的词性
t(yi-1, yi, x, i)就表示的是句子x中第i-1个单词标注的词性yi-1到第i个单词标注的词性yi这么一个情况,加上权重λ后λt(yi-1, yi, x, i)就表示的是第i-1个单词标注为词性yi-1到第i个单词标注为词性yi的可能性,例如动词后面接名词的可能性较大,接动词可能性较小
s(yi, x, i)表示的是句子x中第i个单词标记为词性为yi的这么一个情况,加上权重μ后μs(yi, x, i)表示的是第i个单词被标注为词性yi的可能性
CRF简单例子:
输入观察序列为X = (X1, X2, X3),输出标记序列为 Y = (Y1, Y2, Y3), Y1, Y2, Y3 的取值空间为 {1, 2}。特征函数如下:
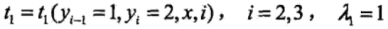
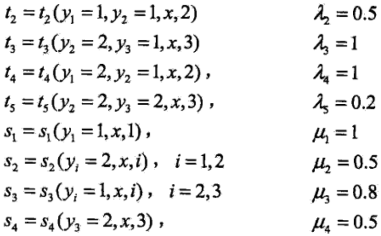
t1~t5表示5个转移函数,对应的权值为λ1~λ5;s1~s4表示4个状态函数,对应的权值为μ1~μ4。tk和sk满足特征条件时取值为1,否则为0。
上面这些式子其实就表示下面这个图:

比如某一个序列y = (y1, y2, y3) = (1, 2, 2),那么这个序列出现的非规范化条件概率(即没有除以规范化因子的条件概率)就是μ1*s1+λ1*t1+μ2*s2+λ5*t5+μ4*s4 = 3.2 (按照图上的顺序走就可以了)
由于某个序列它没有经过的路线或者状态对应的tk和sk的值都为0,所以所有可能的序列的非规范化条件概率(即没有除以规范化因子的条件概率)均可以表示为:
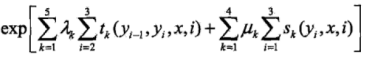
第一项k从1到5表示t1~t5这5个转移函数以及对应的权值λ1~λ5,第二项k从1到4表示s1~s4这4个状态函数以及对应的权值μ1~μ4,tk和sk满足特征条件时取值为1,否则为0。



