DS博客作业01--线性表

[DS博客作业01--线性表]

这个作业属于哪个班级	数据结构--网络2011/2012
这个作业的地址	DS博客作业01--查找
这个作业的目标	学习线性表的相关结构
姓名	姚庆荣
目录 [DS博客作业01--线性表] 0. PTA得分截图 1.本周学习总结（5分） 1.1 绪论(1分) 1.1.1 数据结构有哪些结构，各种结构解决什么问题？ 1.1.2 时间复杂度及空间复杂度概念。 1.1.3 时间复杂度有哪些？如何计算程序的时间复杂度和空间复杂度，举例说明。 1.2 线性表(1分) 1.2.1 顺序表 1.2.2 链表(2分) 1.2.3 有序表及单循环链表(1分) null 2.PTA实验作业（4分） 2.1 两个有序序列的中位数 2.1.1 解题思路及伪代码 2.1.2 总结解题所用的知识点 2.2 一元多项式的乘法与加法运算 2.2.1 解题思路及伪代码 2.2.2 总结解题所用的知识点 3.阅读代码（1分） 3.1 题目及解题代码 3.2 该题的设计思路 3.3 分析该题目解题优势及难点。

0. PTA得分截图

1.本周学习总结（5分）

1.1 绪论(1分)

1.1.1 数据结构有哪些结构，各种结构解决什么问题？

逻辑结构（图表和二元组）：

集合：元素同属一个集合；

线性结构：数据元素关系一对一，除开始元素和终端元素唯一外，其余元素都仅有一个前驱元素和一个后继元素；

树形结构：数据元素关系一对多，除开始元素唯一，终端元素不唯一，其余元素有一个或多个后继元素；

图形结构：数据元素关系一对多，开始和终端元素数量任意，且其余元素的前驱元素和后继元素可有多个；

存储结构：

顺序存储结构：采用一组连续的存储单元存放所以数据元素；

链式存储结构：每个元素有一个对应的内存结点，结点地址不一定连续，通过指针链接结点；

1.1.2 时间复杂度及空间复杂度概念。

计算算法的频度T(n)：T(n)与计算算法执行的时间成正比，与操作时间大致相同；

时间复杂度O(n)：T(n)=O(f(n))，也称渐进时间复杂度，随问题规模n的增大，算法执行时间的增长率与f(n)的增长率相同；是对时间增加趋势的分析；

空间复杂度S(n)：S(n)=O(g(n))，是对一个算法在运行过程中临时占用存储空间大小的量度；只考虑临时空间；

1.1.3 时间复杂度有哪些？如何计算程序的时间复杂度和空间复杂度，举例说明。

时间复杂度的种类：常数阶O(1),对数阶O(),线性阶O(n),线性对数阶O(nlog2n),平方阶O(n^{2)，立方阶O(n}3),...，k次方阶O(n^{k),指数阶O(2}n)；

例：

int i=0;
int j=0;
while(i<n){
  while(j<n){
    j++;
  }
  i++;
}

算法计算的时间为两层n循环，时间复杂度与最高的次方阶有关，时间复杂度为O(n^{2)，空间复杂度也为O(n}2);

1.2 线性表(1分)

1.2.1 顺序表

介绍顺序表结构体定义、顺序表插入、删除的代码操作

定义：

/*线性表的定义*/
typedef struct
{
       char *elem;
       int length;//当前长度
       int listsize;//线性表的长度
}SqList;

插入：

void Insert(sq_list_ *l,int i, int x) {
	//先判满，看顺序表是否还有空间能装得下新元素
	if (l->length >= MAX) {
		std::cout << "\nthe list is full!\n";
		return;
	}
	//然后判断选择插入的索引位置是否合理
	//已有元素的索引为0---length-1，所以插入元素的范围只能是 0---length,
	if (i<0 || i>l->length) {
		std::cout << "\ninvalid index: "<<i<<"! the index should be 0 - "<< l->length<<" \n";
	}
	//把i位置及其之后的元素都后移一位
	int j;
	for (j = l->length - 1; j > i; j--)
		l->data[j + 1] = l->data[j];
	l->data[i] = x;//在i位置赋值x
	l->length++;//更新表长
}

删除：

void Delete(sq_list_ *l, int i) {
	//判空
	if (l->length<=0) {
		std::cout << "\the list is empty!\n";
		return;
	}
	if (i<0 || i>l->length - 1) {
		std::cout << "\ninvalid index: "<<i<<"! the index should be 0 - " << l->length-1 << " \n";
		return;
	}
	for (int j = i; j < l->length - 1; j++)
		l->data[j] = l->data[j + 1];

	l->length--;
}

介绍顺序表插入、删除操作时间复杂度

如果插入和删除的是最后一个元素，那么时间复杂度是O（1）；

如果是插入和删除的是第一个元素，那么时间复杂度是O ( n )；

如果是插入和删除的是第i个元素，那么时间复杂度是O(n-i);

所以顺序表时间复杂度O(n)。

1.2.2 链表(2分)

画一条链表，并在此结构上介绍如何设计链表结构体、头插法、尾插法、链表插入、删除操作

结构体：

typedef struct Node
{
ElemType data;
struct Node *next;
}Node;

头插法：

oid CreateList_b(LinkList Lb)            //头插法 
{
    int s_f,flag=1;
    Node *p;
    p=Lb;
    printf("Please enter Lb data and enter 0 over:\n") ;
    while(flag)
    {
        scanf("%d",&s_f);
        if(s_f!=0)
        {
            p=(LinkList)malloc(len);
            p->data=s_f;
            p->next=Lb->next;
            Lb->next=p;
        }
        else
            flag=0;
    }
}

尾插法：

void CreateList_a(LinkList La)          //尾插法 
{
    int s_f,flag=1;
    Node *p1,*p2;
    p1=La;
    printf("Please enter La data and enter 0 over:\n") ;
    while(flag)
    {
        scanf("%d",&s_f);
        if(s_f!=0)
        {
            p2=(LinkList)malloc(len);
            p2->data=s_f;
            p1->next=p2;
            p1=p2;
        }
        else
        {
            flag=0;
            p1->next=NULL;
        }
    }
}

链表删除：

void deleteLinkedList(LinkedList L,int i)//删除链表上的元素
{
    int j;
     LinkedList p,q;
     p=L;
     j=1;
     while(j<i)
     {
         p=p->next;
         j++;
     }
     q=p->next;
     p->next = p->next->next;
     free(q);
}

重构链表如何操作？链表操作注意事项请罗列。
1. 链表的非空判断；
2. 对链表结点的next关系进行修改之前，一般注意保留后继结点；
  链表有无头结点；
3. 遍历时要记住新建遍历指针，一般不要将指向头结点的头指针拿去当遍历指针;
4. 链表的类型：单链表，循环单链表，循环双链表等；
5. 删除结点后，记得delete；
链表及顺序表在存储空间、插入及删除操作方面区别，优势？

1.2.3 有序表及单循环链表(1分)

有序顺序表插入(以递增为例)：

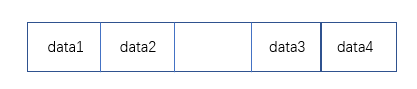
代码：

    // insert_num  为插入的数据
    int position = 0;    // 存放要插入的位置

    for(i = L->length - 1; i >= 0 && L->data[i] < insert_num; i--)
    {
         L->data[i + 1] = L->data[i];
    }
    position = i+1;    //找位置

    L->data[position] = insert_num;    //插入
    L->length++;    //增加长度

有序单链表插入、删除(以递增为例)：

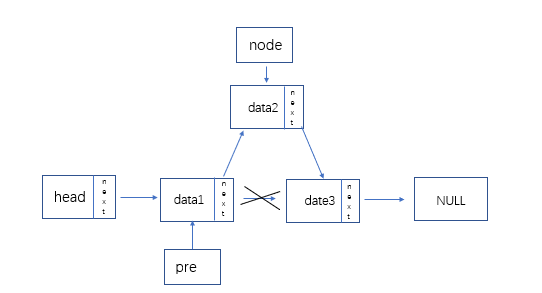
代码：

    LinkList pre = L;
    while(pre->next && pre -> next > insert_num )  //遍历，寻找插入位置的前驱
    {
         pre = pre->next;
    }
    
    LinkList node = new LNode;    //新建结点，存放插入数据
    node->data = insert_num;
    
    node->next = pre->next;     //修改next关系，完成插入
    pre->next = node;

有序链表合并：

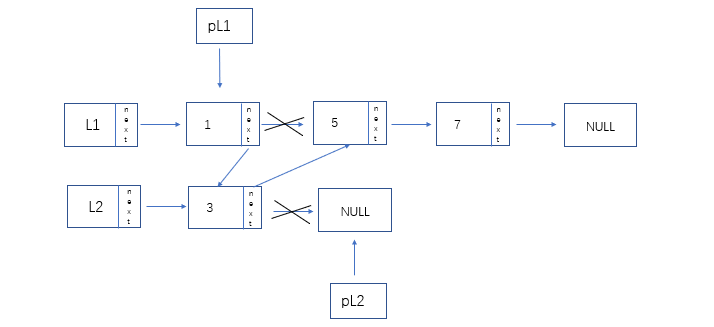
代码：

     LinkList pL1 = L1->next;    //新建遍历指针
     LinkList pL2 = L2->next;

     LinkList merge_L = L;      //重构链表
     L->next = NULL;

     while(pL1 && pL2)          //任一为空时结束循环
     {
          if(pL1->data == pL2->data)  //相同
          {
               merge_L -> next = pL1;
               merge_L = merge->next;

               pL1 = pL1 ->next;
               pL2 = pL2 ->next;
          }
          else if(pL1->data < pL2->data)  
          {
               merge_L -> next = pL1;
               merge_L = merge->next;
                
              pL1 = pL1 ->next;
          }
          else 
          {
               merge_L -> next = pL2;
               merge_L = merge->next;

               pL2 = pL3->next;
          }
     }

      if(pL1)    //若pL1所指向为空，则pL2剩下的数据元素接到merge_L的后面
          merge_L ->next = pL2;
      else
          merge_L ->next = pL1;

有序链表合并的优势：

1)有序顺序表合并需要新建一个数组；有序链表可以在原链表上进行重构，更节省空间

2)若合并的某个表先为空，有序顺序表需要将剩下的元素遍历存入重构数组中；而有序链表仅仅修改next关系即可

单循环链表特点，循环遍历方式：

特点：
1）尾结点的next不指向NULL，而是指向头结点
2）可以从任何位置开始遍历整个链表
遍历：

    LinkList p = L->next;  
    while(p != L)    //与单链表不同的是，将 p!= NULL 改为了p!= L
    {
         ...
         p = p->next;
    }

2.PTA实验作业（4分）

2.1 两个有序序列的中位数

2.1.1 解题思路及伪代码

定义 S1，S2， total；

输入长度N；

for(i=0 to n)

输入集合S1

end for

for(i=0 to n)

输入集合S2

end for

for（t=0 to t<2*n)

if(对应S2中元素大于等于S1)

total[]=S1[];

end if

else if(对应S2中元素小于于S1)

total[]=S2[];

end if

end for

输出中位数；

2.1.2 总结解题所用的知识点

未使用链表的方式进行编码，使用c中的for循环语句和if语句的不同情况进行判断，计算出中位数。

2.2 一元多项式的乘法与加法运算

2.2.1 解题思路及伪代码

// 多项式合并：
LinkList MergeList(LinkList L1, LinkList L2)
{
        pL1 = L1 ->next;
        pL2 = L2 -> next; 
        tail = L1;        

        L_merge = L1;
        L_merge->next = NULL;
        
        while(pL1 != NULL && pL2 != NULL)  do
        {
            if( pL1 -> index = pL2 ->index)  //如果指数相等
            {
                   pL1->coefficient = pL1->coefficient + pL2->coefficient;//系数相加，存放在pL1中
                   再将pL1所指的结点接到tail后面；
                   tail = tail->tail;    //tail移动
                   pL1、pL2移动；
             }end if
              
             else if (pL1 ->index > PL2 ->index) 
             {
                   将pL1所指的结点接到tail后面；
                   tail = tail->tail;    //tail移动
                   pL1移动；
             } end else if

           //...pL2所指结点的指数大时，处理情况与pL1大类似，不多赘述
        }end while
      
        if(pL1)  //如果while循环结束，pL1仍剩余
            tail ->next = pL1;
        end if
        else 
             tail ->next = pL2;
        end else

        return L_merge;  //返回头结点
}



// 多项式相乘：
LinkList MultiplyList(LinkList L1, LinkList L2)
{
     新建LinkList指针L_multiply（头结点）存放最终相乘后的多项式
     新建LinkList指针L_temp，存放计算过程中多项式

      while(pL1)
      {
            L_temp->NULL;      //每轮开始时，重构L_temp;
            tail = L_temp;
            pL2 = L2->next;    //每轮初始化pL2
  
            while(pL2)
            {
                  新建node结点，并分配内存；
                //node的介绍：node结点存放pL1所指的数据与pL2所指的数据相乘；
  
                  node->index = pL1->index + pL2->index;
	          node->coefficient = pL1->coefficient * pL2->coefficient;
              
                  将node接到tail后面；
                  tail、pL2移动到后一个结点
            }
            tail -> next = NULL;  //尾结点的next为空
            将pL1移动到后一位  
      
            调用函数MergeList()，将L_multiply和L_temp合并，
            合并后的多项式在L_multiply中
      }end while
       return L_multiply;
}end while

2.2.2 总结解题所用的知识点

多项式合并，用到了链表合并的知识点：链表重构，尾插法、链表遍历
多项式相乘，用到了尾插法新建链表、调用函数

3.阅读代码（1分）

3.1 题目及解题代码

题目描述

判断给定的链表中是否有环。如果有环则返回true，否则返回false。

class Solution {
public:
    bool hasCycle(ListNode *head) {
        ListNode* fast = head;
        ListNode* slow = head;
        while(slow!=NULL&&fast->next!=NULL&&fast->next->next!=NULL)
        {
            fast = fast->next->next;
            slow = slow->next;
            if(fast==slow)
            {
                return true;
            }
        }
        return false;
    }
};

3.2 该题的设计思路

设计思路：

使用快慢指针，指针p1每次移动一个结点，指针p2每次移动2个结点，若p1、p2相遇则证明环存在

算法的时间复杂度：算法中涉及一个循环，时间复制度为O(n)
空间复杂度：临时变量占用的临时存储空间与问题规模无关，空间复制度为O(1)

3.3 分析该题目解题优势及难点。

题解优势：使用了快指针和慢指针解决了分析链表是否有环的问题。
延申：在查找倒数第k个数据元素时也可以使用类似的两个指针遍历的方式：一个指针1先走k个位置，之后指针2再和指针1一起开始移动，当指针1为空时，指针2所指的数据元素就是倒数第k个元素。
难点：是否考虑到快慢指针的使用

posted on 2021-06-14 18:04 姚庆荣阅读(15) 评论(0) 编辑收藏举报