SPFA最短路径算法详解

算法思路

 用一个队列储存当前可能用于更新邻接

点的点，每次取出队首更新邻接点，若邻接点能被

更新，则把该点塞进队列（保证队列中没有相同的

点）。

 看起来是个很不靠谱的算法，SPFA 只能在随机数据

下或者在某些 DP 模型中运行良好。

 下面我们通过『怎样卡SPFA』来理解这个算法的问

题到底在哪

知识点 – 怎样卡 SPFA

 第一种卡法其实和卡写错的 Dijkstra 的方法一样：

 SPFA 虽然保证点不会重复，但不能保证一个点不会多次入队。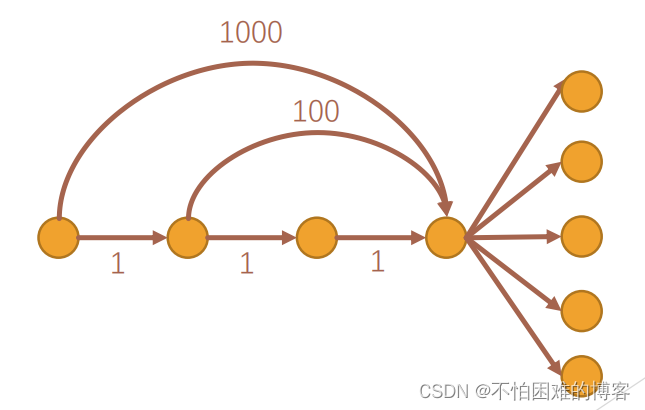

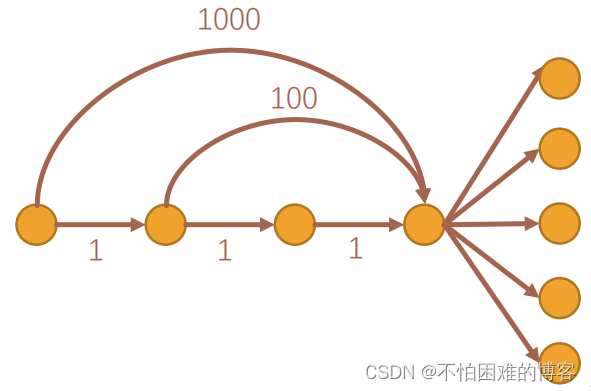
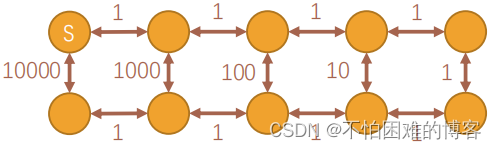
 第二种是网格图。

 SPFA 并没有规定点入队出队的顺序，它更像是 BFS。

我们只需要骗 SPFA 作很多次无效的更新即可（也就

是更新很多次但是没有得到最终答案）。

 代码实现：

void spfa(const int &st_point) 
{
	memset(dst, 0x3f, sizeof dst);
	std::queue<int> que;
	dst[st_point] = 0;
	que.push(st_point), isfix[st_point] = true;
	while (!que.empty()) 
	{
		int u = que.front();
		que.pop(), isfix[u] = false;
		for (int it = grp[u]; it; it = grp.nxt[it]) 
		{
			int v = grp.lnk[it];
			if (dst[v] > dst[u] + grp.wgt[it])
			{
				dst[v] = dst[u] + grp.wgt[it];
				if (!isfix[v]) isfix[v] = true, que.push(v);
			}
		}  
	} 
}

问题 K: 【一本通图 最短路径算法】最短路(Spfa)

[题目描述]

#include <stdio.h>
#include <string.h>
#define INF 999999999;
struct node
{
    int to, next, w;
}e[1001000];
int q[1000100], h, t, cnt = 0, head[100100], vis[100010], d[100010];
void add(int u, int v, int w)
{
    cnt++;
    e[cnt].to = v;
    e[cnt].w = w;
    e[cnt].next = head[u];
    head[u] = cnt;
    cnt++;
    e[cnt].to = u;
    e[cnt].w = w;
    e[cnt].next = head[v];
    head[v] = cnt;
}
int main()
{
    int n, m, i, j, u, v, w, b;
    memset(head, 0, sizeof(head));
    memset(vis, 0, sizeof(vis));
    scanf("%d%d", &n, &m);
    for(i = 1; i <= m; i++)
    {
        scanf("%d%d%d", &u, &v, &w);
        add(u, v, w);
    }
    for(i = 1; i <= n; i++)
        d[i] = INF;
    d[1] = 0;
    h = t = 1;
    q[t] = 1;
    vis[1] = 1;
    t++;
    while(h < t)
    {
        u = q[h];
        b = head[u];
        while(b != 0)
        {
            v = e[b].to;
            if(d[v] > d[u] + e[b].w)
            {
                d[v] = d[u] + e[b].w;
                if(vis[v] == 0)
                {
                    vis[v] = 1;
                    q[t] = v;
                    t++;
                }
            }
            b = e[b].next;
        }
        vis[u] = 0;
        h++;
    }
    printf("%d\n", d[n]);
    return 0;
}