分治算法C++习题练习
因为本文章是习题练习，所有不会有具体讲解。如想看具体的思路讲解，请在我的博客中找到分治算法详解（带图）,或者访问
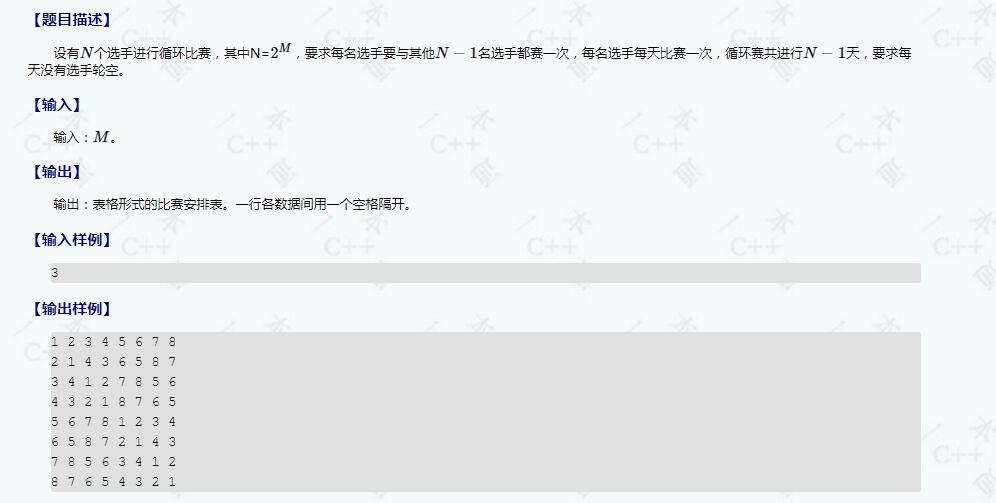
问题 A: 【一本通基础分治】循环比赛日程表
[题目描述]
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1024, MAXM = 1024;
int matchlist[MAXN][MAXN];
int m;
int main()
{
scanf("%d", &m);
int n = 1 << m, k = 1, half = 1;//变量half表示当前方阵的大小，也是要生成的下一个方阵的大小的一半
matchlist[0][0] = 1;
while(k <= m)
{
for(int i = 0; i < half; i++)//构造右上方方阵
{
for(int j = 0; j < half; j++)
{
matchlist[i][j + half] = matchlist[i][j] + half;
}
}
for(int i = 0; i < half; i++)//对称交换构造下半部分方阵
{
for(int j = 0; j < half; j++)
{
matchlist[i + half][j] = matchlist[i][j + half];//左下方方阵等于右上方方阵
matchlist[i + half][j + half] = matchlist[i][j];//右下下方方阵等于左上上方方阵
}
}
half *= 2;
k++;
}
for(int i = 0; i < n; i++)
{
for(int j = 0; j < n; j++)
{
printf("%d ", matchlist[i][j]);
}
putchar('\n');
}
}问题 B: 【一本通基础分治】 取余运算
[题目描述]
输入三个正整数a,b,c计算a^b mod c。
数据范围：100%的数据满足：a,b,c在longint范围内。
输入
第一行输入三个正整数a,b,c。
输出
输出a^b mod c的值。
样例输入
2 3 5
样例输出
3
#include <bits/stdc++.h>
using namespace std;
long long b, p, k, a;
long long f(long long p)
{
if(p == 0)
{
return 1;
}
long long temp = f(p / 2) % k;
temp = (temp * temp) % k;
if(p % 2 == 1)
{
temp = (temp * b) % k;
}
return temp;
}
int main()
{
cin >> b >> p >> k;
b %= k;
printf("%d\n", f(p));
return 0;
}
问题 C: 【一本通基础分治】黑白棋子的移动
[题目描述]
有2n个棋子（n≥4）排成一行，开始为位置白子全部在左边，黑子全部在右边，如下图为n=5的情况：
○○○○○●●●●●
移动棋子的规则是：每次必须同时移动相邻的两个棋子，颜色不限，可以左移也可以右移到空位上去，但不能调换两个棋子的左右位置。每次移动必须跳过若干个棋子（不能平移），要求最后能移成黑白相间的一行棋子。如n=5时，成为：
○●○●○●○●○●
任务：编程打印出移动过程。
输入
一个整数
输出
移动过程
样例输入
7
样例输出
step 0:ooooooo*******-- step 1:oooooo--******o* step 2:oooooo******--o* step 3:ooooo--*****o*o* step 4:ooooo*****--o*o* step 5:oooo--****o*o*o* step 6:oooo****--o*o*o* step 7:ooo--***o*o*o*o* step 8:ooo*o**--*o*o*o* step 9:o--*o**oo*o*o*o* step 10:o*o*o*--o*o*o*o* step 11:--o*o*o*o*o*o*o*
#include <bits/stdc++.h>
using namespace std;
int n, step = 0, space = 0;
char c[101];
void print()//打印答案
{
cout << "step " << step << ":";
for(int i = 1; i <= 2 * n + 2; i++)
{
cout << c[i];
}
cout << endl;
step++;
}
void init(int n)//初始化
{
int i;
step = 0;
space = 2 * n + 1;
for(i = 1; i <= n; i++)
{
c[i] = 'o';
}
for(i = n + 1; i <= 2 * n; i++)
{
c[i] = '*';
}
c[2 * n + 1] = '-';
c[2 * n + 2] = '-';
print();
}
void move (int k)//实现每一步的移动，并打印
{
int j;
for(j = 0; j <= 1; j++)
{
c[space + j] = c[k + j];
c[k + j] = '-';
}
space = k;
print();
}
void mv(int n)//主要指令
{
int i, k;
if(n == 4)
{
move(4);
move(8);
move(2);
move(7);
move(1);
}
else
{
move(n);
move(2 * n - 1);
mv(n - 1); //递归实现
}
}
int main()
{
cin >> n;
init(n);//初始化。
mv(n);
return 0;
}问题 D: 【一本通基础分治】光荣的梦想
【题目描述】
Prince对他在这片大陆上维护的秩序感到满意，于是决定启程离开艾泽拉斯。在他动身之前，Prince决定赋予King_Bette最强大的能量以守护世界、保卫这里的平衡与和谐。在那个时代，平衡是个梦想。因为有很多奇异的物种拥有各种不稳定的能量，平衡瞬间即被打破。KB决定求助于你，帮助他完成这个梦想。
一串数列即表示一个世界的状态。
平衡是指这串数列以升序排列。而从一串无序数列到有序数列需要通过交换数列中的元素来实现。KB的能量只能交换相邻两个数字。他想知道他最少需要交换几次就能使数列有序
【输入】
第一行为数列中数的个数n,第二行为n ≤ 1000000个数。表示当前数列的状态。
【输出】
输出一个整数，表示最少需要交换几次能达到平衡状态。
【输入样例】
4
2 1 4 3
【输出样例】
2
#include <bits/stdc++.h>
using namespace std;
long long n, a[1000001], p[1000001], s;
void msort(int l, int r)
{
if(l == r)
return;
int mid = (l + r) / 2;
msort(l, mid);
msort(mid + 1, r);
int i = l, j = mid + 1, k = l;
while(i <= mid && j <= r)
{
if(a[i] <= a[j])
{
p[k++] = a[i++];
}
else
{
s += (mid - i + 1);
p[k++] = a[j++];
}
}
while(i <= mid)
{
p[k++] = a[i++];
}
while (j <= r)
{
p[k++] = a[j++];
}
for(i = l; i <= r; i++)
{
a[i] = p[i];
}
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
}
msort(1, n);
cout << s << endl;
return 0;
}
问题 E: 【一本通基础分治】2011
[题目描述]
已知长度最大为200位的正整数n，请求出2011n的后四位。
输入
第一行为一个正整数k，代表有k组数据（k≤200），接下来的k行，每行都有一个正整数n，n的位数≤200。
输出
每一个n的结果为一个整数占一行，若不足4位，去除高位多余的0。
样例输入
3 5 28 792
样例输出
1051 81 5521
#include <bits/stdc++.h>
using namespace std;
int a[502],b[201];
char ch[202];
int main()
{
int n = 0;
int q = 2011, k, i, l, j, x, t, z;
do
{
n += 1;
a[n] = q;
q = q * 2011 % 10000;
}while(q != 2011);
a[0] = a[n];
cin >> k;
for(i = 1; i <= k; i++)
{
j = 0, x = 0, t = 0;
memset(b, 0, sizeof(b));
scanf("%s", &ch);
l = strlen(ch);
for(z = 0; z < l; z++)
b[z + 1] = ch[z] - 48;
while(j < l)
{
j += 1;
x = (x * 10 + b[j]) % n;
}
cout << a[x] << endl;
}
return 0;
}