dp基础模型习题练习大全
问题 A: 【一本通基础DP基础模型】【例9.2】数字金字塔
【题目描述】
观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。
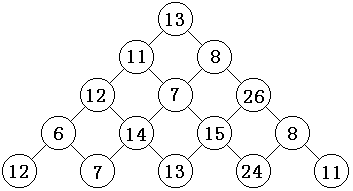
在上面的样例中,从13到8到26到15到24的路径产生了最大的和86。
【输入】
第一个行包含R(1≤ R≤1000)，表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
所有的被供应的整数是非负的且不大于100。
【输出】
单独的一行，包含那个可能得到的最大的和。
【输入样例】
5
13
11 8
12 7 26
6 14 15 8
12 7 13 24 11
【输出样例】
86
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1005;
int a[MAXN][MAXN], f[MAXN][MAXN], n;
int main()
{
//读入
cin >> n;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= i; j++)
{
cin >> a[i][j];
}
}
//初始化
f[1][1] = a[1][1];
//随时更新f[i][j]
for(int i = 2; i <= n; i++)
{
for(int j = 1; j <= i; j++)
{
f[i][j] = max(f[i - 1][j - 1], f[i - 1][j]) + a[i][j];
}
}
int ans = 0;
//比较ans和f[n][i]
for(int i = 1; i <= n; i++)
{
ans = max(ans, f[n][i]);
}
cout << ans << endl;
return 0;
} 本OJ资源来自于互联网，如有侵权请来信告知，accoders@aliyun.com邮箱
问题 B: 【一本通基础DP基础模型】【例9.3】求最长不下降序列
[题目描述]
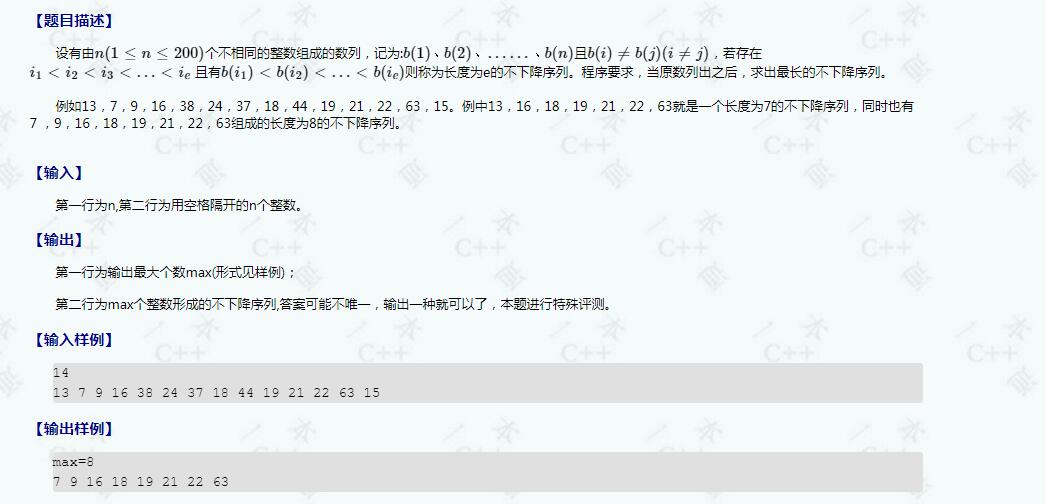
#include <bits/stdc++.h>
using namespace std;
const int N = 1001;
int a[N], f[N], c[N];
int main()
{
int n, maxx = -23333333;
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
}
int k;
for(int i = 1; i <= n; i++)
{
f[i] = 1;
for(int j = 1; j < i; j++)
{
if(a[j] <= a[i] && f[j] + 1 > f[i])
f[i] = f[j] + 1;
}
if(f[i] > maxx)
{
maxx = f[i];
k = i;
}
}
int q = 0, m = maxx, i = k - 1;
c[q++] = k;
while(m > 1)
{
if(f[i] == m - 1 && a[i] <= a[k])
{
c[q++] = i;
k = i;
m--;
}
i--;
}
printf("max=%d", maxx);
cout << endl;
for(int i = q - 1; i >= 0; i--)
{
printf("%d ", a[c[i]]);
}
return 0;
}问题 C: 【一本通基础DP基础模型】【例9.4】NOIP 1999防御导弹
[题目描述]
某国为了防御敌国的导弹袭击，发展出一种导弹拦截系统。但是这种导弹拦截 系统有一个缺陷：虽然它的第一发炮弹能够达到任意的高度，但是以后每一发炮弹都不能高于前一发的高度。某天，雷达捕捉到敌国的导弹来袭。由于该系统还在试 用阶段，所以只有一套系统，因此有可能不能拦截所有的导弹。
输入
最多20个整数，分别表示导弹依次飞来的高度（雷达给出高度数据是不大于30000的正整数）
输出
第一行 整数M。表示：这套系统最多能拦截 M 枚导弹.
第二行 一个整数，要拦截所有导弹最少要配备的系统数
样例输入
389 207 155 300 299 170 158 65
样例输出
6 2
#include <bits/stdc++.h>
using namespace std;
int f[1001], p[1001], a[1001];
int n;
int main()
{
int maxn, ans, k, s;
int u = 1;
while(cin >> a[u])
{
u++;
}
n = u - 1;
f[n] = 1;
for(int i = n - 1; i >= 1; i--)
{
maxn = 0;
k = 0;
for(int j = i + 1; j <= n; j++)
{
if(a[i] >= a[j])
{
if(f[j] > maxn)
{
maxn = f[j];
k = j;
}
}
}
f[i] = maxn + 1;
p[i] = k;
}
ans = 0;
for(int i = 1; i <= n; i++)
{
if(f[i] > ans)
{
ans = f[i];
}
}
// for(int i = 1; i <= n; i++)
// {
// cout << f[i] << endl;
// }
//
cout << ans << endl;
int cnt = 1;
int g[2000];
int minn = 10000000;
int m = 0;
int k1 = 1;
g[1] = a[1];
for(int i = 2; i <= n; i++)
{
m = 0;
for(int j = 1; j <= k1; j++)
{
if(g[j] >= a[i])
{
if(m == 0)
m = j;
else if(g[j] < g[m])
m = j;
}
}
if(m == 0)
{
g[++k1] = a[i];
}
else
{
g[m] = a[i];
}
}
cout << k1 << endl;
// while(s != 0)
// {
// cout << a[s] << " ";
// s = p[s];
// }
return 0;
}问题 D: 【一本通基础DP基础模型】【例9.6】 挖地雷
[题目描述]
在一个地图上有N个地窖（N<=200）,每个地窖中埋有一定数量的地雷。同时，给出地窖之间的连接路径，并规定路径都是单向的。某人可以从任一处开始挖地雷，然后沿着指出的连接往下挖（仅能选择一条路径），当无连接时挖地雷工作结束。设计一个挖地雷的方案，使他能挖到最多的地雷。
输入
N {地窖的个数}
W1，W2，……WN {每个地窖中的地雷数}
X1，Y1 {表示从X1可到Y1}
X2，Y2
……
0，0 {表示输入结束}
保证x<y
输出
K1——K2——……——Kv {挖地雷的顺序}
MAX {最多挖出的地雷数}
样例输入
6 5 10 20 5 4 5 1 2 1 4 2 4 3 4 4 5 4 6 5 6 0 0
样例输出
3-4-5-6 34
#include <bits/stdc++.h>
using namespace std;
int f[201], c[201], w[201];
bool a[201][201];
int main()
{
int n;
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> w[i];
}
memset(a, false, sizeof(a));
memset(c, 0, sizeof(c));
int x, y, long1 = 0, next = 0;
do
{
cin >> x >> y;
if((x != 0) && (y != 0))
{
a[x][y] = true;
}
}while((x != 0) || (y != 0));
f[n] = w[n];
for(int i = n - 1; i >= 1; i--)
{
long1 = 0;
next = 0;
for(int j = i + 1; j <= n; j++)
{
if((a[i][j]) && (f[j] > long1))
{
long1 = f[j];
next = j;
}
}
f[i] = long1 + w[i];
c[i] = next;
}
next = 1;
for(int u = 2; u <= n; u++)
{
if(f[u] > f[next])
{
next = u;
}
}
int maxx = f[next];
cout << next;
next = c[next];
while(next != 0)
{
cout << "-" << next;
next = c[next];
}
cout << endl;
cout << maxx << endl;
// for(int i = 1; i <= n; i++)
// {
// cout << f[i] << " " << c[i] << endl;
// }
return 0;
}问题 E: 【一本通基础DP基础模型】【例9.7】 友好城市
[题目描述]
Palmia国有一条横贯东西的大河，河有笔直的南北两岸，岸上各有位置不同的N个城市。北岸的每个城市有且仅有一个友好城市在南岸，而且不同城市的友好城市不相同。
每对友好城市都向政府申请在河上开辟一条直线航道连接两个城市，但是由于河上雾太大，政府决定避免任意两条航道交叉，以避免事故。编程帮助政府作出一些批准和拒绝申请的决定，使得在保证任意两条航线不相交的情况下，被批准的申请尽量多。
输入
第1行，一个整数N(1<=N<=50000,表示城市数。
第2行到第n+1行，每行两个整数，中间用1个空格隔开，分别表示南岸和北岸的一对友好城市的左边。(0<=xi<=10000)
输出
仅一行，输出一个整数，政府所能批准的最多申请书。
样例输入
7 22 4 2 6 10 3 15 12 9 8 17 17 4 2
样例输出
4
#include <bits/stdc++.h>
using namespace std;
int x, y, f[50001], n;
struct name
{
int x;
int y;
}city[50001];
bool cmp(name a, name b)
{
return a.x < b.x;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> city[i].x >> city[i].y;
}
sort(city + 1, city + 1 + n, cmp);
for(int i = 1; i <= 50000; i++)
{
f[i] = 1;
}
for(int i = n - 1; i >= 1; i--)
{
for(int j = i + 1; j <= n; j++)
{
if(city[i].y < city[j].y)
f[i] = max(f[j] + 1, f[i]);
}
}
int ans = 0;
for(int i = 1; i <= n; i++)
{
if(ans < f[i])
{
ans = f[i];
}
}
cout << ans << endl;
return 0;
}问题 F: 【一本通基础DP基础模型】【例9.8】 合唱队形
[题目描述]
N位同学站成一排，音乐老师要请其中的(N-K)位同学出列，使得剩下的K位同学排成合唱队形。
合唱队形是指这样的一种队形：设K位同学从左到右依次编号为1, 2, …, K，他们的身高分别为T1, T2, …, TK，则他们的身高满足T1 < T2 < … < Ti , Ti > Ti+1 > … > TK (1 <= i <= K)。
你的任务是，已知所有N位同学的身高，计算最少需要几位同学出列，可以使得剩下的同学排成合唱队形。
输入
第一行是一个整数N（2 <= N <= 100），表示同学的总数。第一行有n个整数，用空格分隔，第i个整数Ti（130 <= Ti <= 230）是第i位同学的身高（厘米）。
输出
包括一行，这一行只包含一个整数，就是最少需要几位同学出列。
样例输入
8 186 186 150 200 160 130 197 220
样例输出
4
#include <bits/stdc++.h>
using namespace std;
int n;
int bxj[101];//以第i位同学为终点的最长不下降序列的长度
int bss[101];//以第i位同学为起点的最长不上升序列的长度
int t[101];
int main()
{
int maxn = 0;
scanf("%d", &n);
for(int i = 1; i <= n; i++)
{
scanf("%d", &t[i]);
}
// memset(bss, 1, sizeof(bss));
// memset(bxj, 1, sizeof(bxj));
bxj[1] = 1;
bss[n] = 1;
for(int i = 1; i <= n; i++)
{
maxn = 0;
for(int j = 1; j < i; j++)
{
if(t[i] > t[j])
if(bxj[j] > maxn)
maxn = bxj[j];
}
bxj[i] = maxn + 1;
}
for(int i = n - 1; i >= 1; i--)
{
maxn = 0;
for(int j = i + 1; j <= n; j++)
{
if(t[i] > t[j])
if(bss[j] > maxn)
maxn = bss[j];
}
bss[i] = maxn + 1;
}
maxn = 0;
for(int i = 1; i <= n; i++)
{
if((bxj[i] + bss[i]) > maxn)
maxn = bxj[i] + bss[i];
}
cout << n - maxn + 1 << endl;
// for(int i = 1; i <= n; i++)
// {
// cout << i << " " ;
// }
// cout << endl;
// for(int i = 1; i <= n; i++)
// {
// cout << bxj[i] << " " ;
// }
// cout << endl;
// for(int i = 1; i <= n; i++)
// {
// cout << bss[i] << " " ;
// }
return 0;
}问题 G: 【一本通基础DP基础模型】【例9.9】最长公共子序列
[题目描述]
一个给定序列的子序列是在该序列中删去若干元素后得到的序列。确切地说，若给定序列X=<x1, x2,…, xm>，则另一序列Z=<z1, z2,…, zk>是X的子序列是指存在一个严格递增的下标序列 <i1, i2,…, ik>，使得对于所有j=1,2,…,k有
xij= zj
给定两个序列X=<x1, x2, …, xm>和Y=<y1, y2, … , yn>，要求找出X和Y的一个最长公共子序列。
例如，序列Z=<B,C,D,B>是序列X=<A,B,C,B,D,A,B>的子序列，相应的递增下标序列为<2,3,5,7>。给定两个序列X和Y，当另一序列Z既是X的子序列又是Y的子序列时，称Z是序列X和Y的公共子序列。例如，若X=<A, B, C, B, D, A, B>和Y=<B, D, C, A, B, A>，则序列<B, C, A>是X和Y的一个公共子序列，序列<B, C, B, A>也是X和Y的一个公共子序列。而且，后者是X和Y的一个最长公共子序列，因为X和Y没有长度大于4的公共子序列。
输入
输出
一个非负整数，表示所求得的最长公共子序列的长度。
样例输入
ABCBDAB BDCABA
样例输出
4
#include <bits/stdc++.h>
using namespace std;
char a[201], b[201];
int t[201][201];
int main()
{
cin >> a;
cin >> b;
int a_long = strlen(a);
int b_long = strlen(b);
for(int i = 1; i < b_long; i++)
t[0][i] = 0;
for(int i = 1; i <= a_long; i++)
t[i][0] = 0;
for(int i = 1; i <= b_long; i++)
{
for(int j = 1; j <= a_long; j++)
{
t[i][j] = max(t[i - 1][j], t[i][j - 1]);
if(a[j - 1] == b[i - 1])
t[i][j] = max(t[i][j], t[i - 1][j - 1] + 1);
}
}
// if(t[b_long][a_long] <= 1)
// {
// cout << t[b_long][a_long] - 1 << endl;
// }
// else
// if(t[b_long][a_long] >= 10)
// {
// cout << t[b_long][a_long] << endl;
// }
// else
// {
cout << t[b_long][a_long] << endl;
// }
// for(int i = 0; i <= b_long; i++)
// {
// cout << b[i] << ' ';
// }
// for(int i = 0; i <= b_long; i++)
// {
// for(int j = 0; j <= a_long; j++)
// {
// cout << t[i][j] << " ";
// }
// cout << endl;
// }
return 0;
}
