字符串算法——KMP算法C++详解
简介
KMP 算法是 D.E.Knuth、J,H,Morris 和 V.R.Pratt 三位神人共同提出的,称之为 Knuth-Morria-Pratt 算法,简称 KMP 算法。该算法相对于 Brute-Force(暴力)算法有比较大的改进,主要是消除了主串指针的回溯,从而使算法效率有了某种程度的提高。
提取加速匹配的信息
上面说道 KMP 算法主要是通过消除主串指针的回溯来提高匹配的效率的,那么,它是则呢样来消除回溯的呢?就是因为它提取并运用了加速匹配的信息!
这种信息就是对于每模式串 t 的每个元素 t j,都存在一个实数 k ,使得模式串 t 开头的 k 个字符(t 0 t 1…t k-1)依次与 t j 前面的 k(t j-k t j-k+1…t j-1,这里第一个字符 t j-k 最多从 t 1 开始,所以 k < j)个字符相同。如果这样的 k 有多个,则取最大的一个。模式串 t 中每个位置 j 的字符都有这种信息,采用 next 数组表示,即 next[ j ]=MAX{ k }。
加速信息,即数组 next 的提取是整个 KMP 算法中最核心的部分,弄懂了 next 的求解方法,也就弄懂了 KMP 算法的十之七八了,但是不巧的是这部分代码恰恰是最不容易弄懂的……
void Getnext(int next[], String t)
{
int j = 0, k = -1;
next[0] = -1;
while(j < t.length - 1)
{
if(k == -1 || t[j] == t[k])
{
j++;
k++;
next[j] = k;
}
else k = next[k];
}
}ok,下面咱们分三种情况来讲 next 的求解过程
特殊情况
当 j 的值为 0 或 1 的时候,它们的 k 值都为 0,即 next[0] = 0、next[1] =0。但是为了后面 k 值计算的方便,我们将 next[0] 的值设置成 -1。
当 t[j] == t[k] 的情况
举个例子:
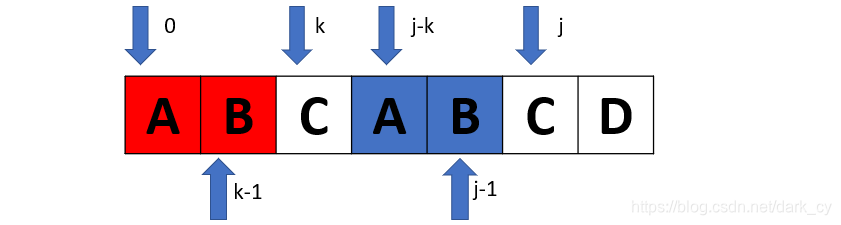
观察上图可知,当 t[j] == t[k] 时,必然有"t[0]…t[k-1]" == " t[j-k]…t[j-1]",此时的 k 即是相同子串的长度。因为有"t[0]…t[k-1]" == " t[j-k]…t[j-1]",且 t[j] == t[k],则有"t[0]…t[k]" == " t[j-k]…t[j]",这样也就得出了next[j+1]=k+1。
当t[j] != t[k] 的情况
关于这种情况,在代码中的描述就是“简单”的一句 k = next[k];。我当时看了之后,感觉有点蒙,于是就去翻《数据结构教程》。但是这本书里,对于这行代码的解释只有三个字:k 回退…!于是我从“有点蒙”的状态升级到了“很蒙蔽”的状态,我心想,k 回退?我当然知道这是 k 退回,但是它为什么要会退到 next[k] 的位置?为什么不是回退到k-1???巴拉巴拉巴拉…此处省略一万字。
我绞尽脑汁,仍是不得其解。于是我就去问百度…
在我看了众多博客之后,终于有了一种拨云见日的感觉,看下图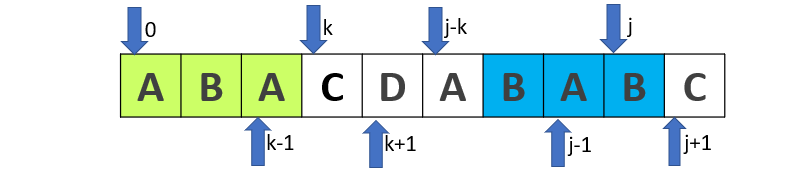
由第2中情况可知,当 t[j] == t[k] 时,t[j+1] 的最大子串的长度为 k,即 next[j+1] = k+1。但是此时t[j] != t[k] 了,所以就有 next[j+1] < k,那么求 next[j+1] 就等同于求 t[j] 往前小于 k 个的字符(包括t[j],看上图蓝色框框)与 t[k] 前面的字符(绿色框框)的最长重合串,即 t[j-k+1] ~ t[j] 与 t[0] ~ t[k-1] 的最长重合串(这里所说“最长重合串”实不严谨,但你知道是符合 k 的子串就行…),那么就相当于求 next[k](只不过 t[k] 变成了 t[j],但是 next[k] 的值与 t[k] 无关)!!!。所以才有了这句 k = next[k],如果新的一轮循环(这时 k = next[k] ,j 不变)中 t[j] 依然不等于 t[k] ,则说明倒数第二大 t[0~next[k]-1] 也不行,那么 k 会继续被 next[k] 赋值(这就是所谓的 k 回退…),直到找到符合重合的子串或者 k == -1。
至此,算是把求解数组 next 的算法弄清楚了(其实是,终于把 k = next[k] 弄懂了…)
因为这个算法神奇难解之处就在k=next[k]这一处的理解上,网上解析的非常之多,有的就是例证,举例子按代码走流程,走出结果了,跟肉眼看的一致,就认为解释了为什么k=next[k];很少有看到解释的非常清楚的,或者有,但我没有仔细和耐心看下去。我一般扫一眼,就大概知道这个解析是否能说的通。仔细想了一天,搞的千转百折,山重水复,一头雾气缭绕的。搞懂以后又觉得确实简单,但是绕人,烧脑。
KMP算法实现
当你求出了 next 数组之后,KMP 算法就很轻易搞定了,下面我用三张图,让你明白 KMP 算法完成匹配的整个过程。
以目标串:s,指针为 i ;模式串:t 指针为 j ; 为例

上图表示:“si-j ~ si-1” == “t 0 ~ t j-1”,s i != t j(前面都相等,但比较到 t j 时发现不相等了)且next[j] == k。
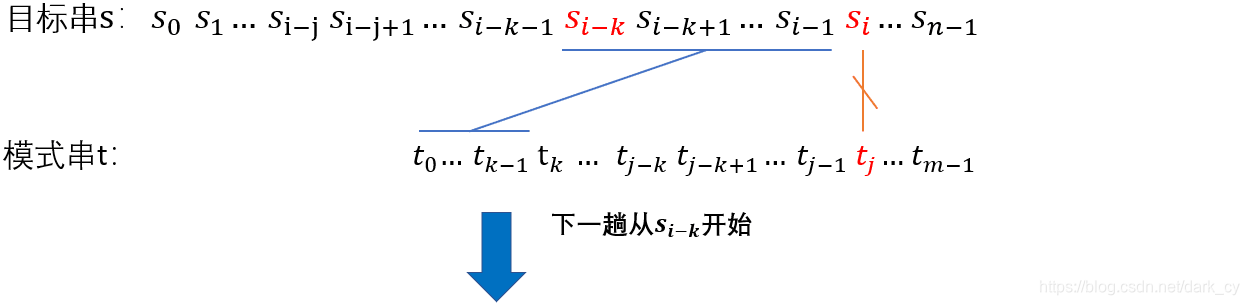
根据 next 数组的定义得知 “t k ~ t j-1” == “t 0 ~ t k-1”,所以 “t 0 ~ t k-1” == “si-k ~ si-1”
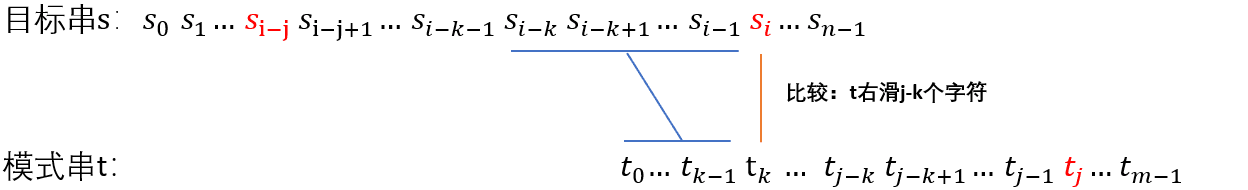
将模式串右移,得到上图,这样就避免了目标穿的指针回溯。
都明了之后就可以手写 KMP 的代码了
int KMP(String s, String t)
{
int next[MaxSize], i = 0, j = 0;
Getnext(t, next);
while(i < s.length && j < t.length)
{
if(j == -1 || s[i] == t[j])
{
i++;
j++;
}
else j = next[j]; //j回退。。。
}
if(j >= t.length)
return (i - t.length); //匹配成功,返回子串的位置
else
return (-1); //没找到
}例题:
问题 A: 【一本通提高篇KMP】剪花布条
[题目描述]
一块花布条,里面有些图案,另有一块直接可用的小饰条,里面也有一些图案。对于给定的花布条和小饰条,计算一下能从花布条中尽可能剪出几块小饰条来呢?
输入
输入中含有一些数据,分别是成对出现的花布条和小饰条,其布条都是用可见ASCII字符表示的,可见的ASCII字符有多少个,布条的花纹也有多少种花样。花纹条和小饰条不会超过1000个字符长。如果遇见#字符,则不再进行工作。
输出
输出能从花纹布中剪出的最多小饰条个数,如果一块都没有,那就老老实实输出0,每个结果之间应换行
样例输入
abcde a3 aaaaaa aa #
样例输出
0 3
解题思路:这道题就是给你一个主串和一个模式串,要求从主串找出没有交集的模式串的最大数量。一开始很容易想到暴力枚举,不过会超时,时间复杂度是O(nm),还不如花多点时间学习新的算法思想,争取在做题中灵活应用。这个算法时间复杂度是O(n+m)
code:
/*
Name: cyr
Copyright:
Author: cyr
Date: 09/08/22 19:51
Description:
这道题就是给你一个主串和一个模式串,要求从主串找出没有交集的模式串的最大数量。
一开始很容易想到暴力枚举,不过会超时,时间复杂度是O(nm).
还不如花多点时间学习新的算法思想,争取在做题中灵活应用。这个算法时间复杂度是O(n+m)
*/
#include <bits/stdc++.h>
#pragma GCC optimize (2)//这个东西按理说没啥用,但是总感觉心里没底,就加了。(也习惯了)
char s[1010], p[1010];
int cnt, next[1010];
using namespace std;
void getnext(int len2)//len2是思路里的模式串长度
{
memset(next, 0, sizeof(next));
int k = 0;
for(int i = 1; i < len2; i++)
{
while(k > 0 && p[k] != p[i])//不断查找,看主串里有没有完整的模式串
k = next[k - 1];
if(p[k] == p[i])
k++;
next[i] = k;
}
}
void kmp(int len1, int len2)//len1是思路里的主串长度,len2是思路里的模式串长度
{
int k = 0;//k是主串和模式串的重合长度
for(int i = 0; i < len1; i++)
{
while(k > 0 && p[k] != s[i])
k = next[k - 1];
if(p[k] == s[i])//只有主串和模式串的元素相等,相等的长度加1
k++;
if(k == len2)//如果主串和模式串的重合长度等于模式串,那就是主串里有一个完整的模式串,cnt++
{
cnt++;
k = 0;//不要忘了k归0,低级错误
}
}
}
int main()
{
while(scanf("%s", s) && s[0] != '#')//碰见#就收工
{
scanf("%s", p);
getnext(strlen(p));
cnt = 0;
kmp(strlen(s), strlen(p));
printf("%d\n", cnt);
}
return 0;
}


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】