线段树详解（C++）

应用场景

假设有这样的问题：有n个数，m次操作，操作分为：修改某一个数或者查询一段区间的值

分析下，如果针对数组元素的修改可以是O(1)完成，求某个区间值需要O(n)才可以完成，如果m和n都很大的情况，这个复杂度就很难接受了。

我们之前学过的前缀和算法可以解决区间求和的问题，并且时间复杂度是O(1)，但如果涉及到修改操作，前缀和数组都需要重新计算，时间复杂度也是O(n)

有没有什么办法可以兼顾以上两种操作，并且可以将时间复杂度降低？

这就是我们要学习的线段树！把修改和查询的时间复杂度都降到O(logn)！！！

算法思想

先来看下线段树长什么样：

有以下数组（为方便计算，数组下标从1开始）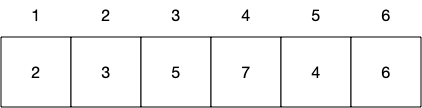

 我们把它转换成线段树，是长这样的：

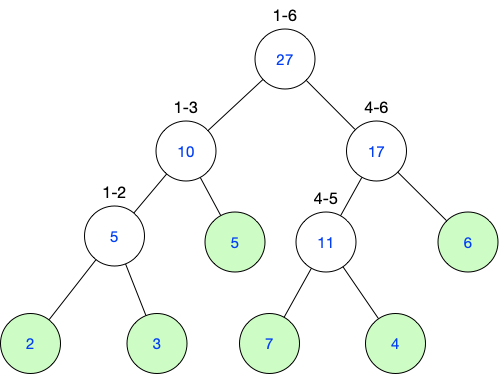
1）叶子结点（绿色）存的都是原数组元素的值

2）每个父结点是它的两个子节点的值的和

3）每个父结点记录它表示区间的范围，如上图的“1-2”表示1到2的区间

下面我们来看看线段树是如何降低操作复杂度的！

查询操作

例如我们需要查询2-5区间的和

 

 

使用递归的思想：

2~5的和

=2~3的和+4~5的和

=3+5+4~5的和

=3+5+11

=19

总之，就是沿着线段树的划分把区间分开，再加到一块就行啦！

修改操作

例如，我们要把结点2的值由3->5，线段树需要沿着红色部分一个一个改，直到根结点：

 

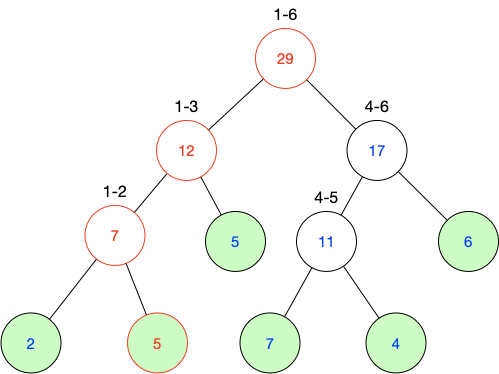
不管是修改操作还是查询操作，时间复杂度都是O(logn)

下一步我们来看怎么实现线段树！

算法实现

首先我们需要将原始数组建立成一颗线段树，然后在树的基础上提供查询和修改的操作。

建树

观察上图，我们发现线段树是一棵近似完全二叉树，利用完全二叉树的性质，我们就可以直接用一个数组来存它。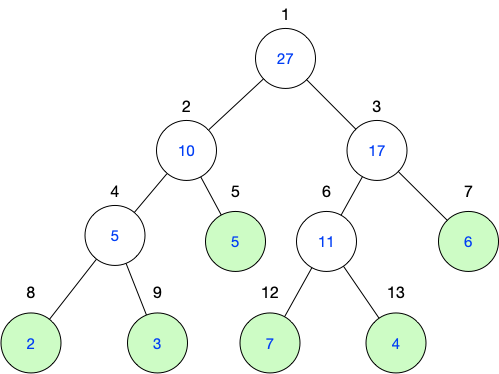

就像上图一样把各个节点标上号，如果根节点编号是n,那它的左子树编号是2n,右子树的编号是2n+1

所以说，知道了根节点的编号，我们就可以快速有效的找到左右子树的根节点

 

void build(int root, int start, int end)
{
    if(start == end)
    {
        tree[root] = num[start];
        return;
    }
    int leftroot = root * 2;
    int rightroot = root * 2 + 1;
    int mid = (start + end) / 2;
    build(leftroot, start, mid);
    build(rightroot, mid + 1, end);
    tree[root] = tree[leftroot] + tree[rightroot];//根结点值=左根+右根
}

查询

int query(int root, int start, int end, int l, int r)
{
    if(l <= start && r >= end)
    {
        return tree[root];
    }
    int leftroot = root * 2;
    int rightroot = root * 2 + 1;
    int mid = (start+end)/2;
    int sum = 0;
    if(l <= mid)
    {
        sum += query(leftroot, start, mid, l, r);
    }
    if(r > mid)
    {
        sum += query(rightroot, mid + 1, end, l, r);
    }
    return sum;
}

修改

/**
* 修改[l,r]区间里的数，都加上k值
*/
void update(int root, int start, int end, int l, int r, int k)
{
    if(start == end)
    {
        tree[root] += k;
        return;
    }
    int leftroot = root * 2;
    int rightroot = root * 2 + 1;
    int mid = (start + end) / 2;
    if(l <= mid)
    {
        update(leftroot, start, mid, l, r, k);
    }
    if(r > mid)
    {
        update(rightroot, mid + 1, end, l, r, k);
    }
    tree[root] = tree[leftroot] + tree[rightroot];
}

！！！：考虑下按区间修改元素值的复杂度？

注意事项：

1）我们在实现线段树时，实际存储肯定大于原始数组，我们一般让tree数组的长度为原始数据长度的3-4倍。

2）本文只是为了让大家学习线段树的实现原理，实际中我们可以将原始数组的start，end使用结构体存储，这样更简洁