前缀和C++超详细讲解(有例题)
前缀和
一维前缀和
如果我单说定义大家可能不理解,所以我打算拿一道例题-795. 前缀和开讲。
【 前缀和与差分】795. 前缀和
输入一个长度为 n 的整数序列。
接下来再输入 m 个询问,每个询问输入一对 l,r。
对于每个询问,输出原序列中从第l 个数到第 r 个数的和。
输入格式
第一行包含两个整数 n 和 m。
第二行包含 n 个整数,表示整数数列。
接下来 m 行,每行包含两个整数l 和 r,表示一个询问的区间范围。
输出格式
共 m 行,每行输出一个询问的结果。
数据范围
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值 ≤1000
输入样例:
5 3
2 1 3 6 4
1 2
1 3
2 4
输出样例:
3
6
10
这道题如果你没有学过前缀和的话,会这么写:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N];
int n, m, r, l, tot;
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i <= m; i++)
{
cin >> l >> r;
tot = 0;
for(int j = l; j <= r; j++)
{
tot += a[j];
}
cout << tot << endl;
}
return 0;
}这样的时间复杂度接近O(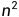 ),会TLE的很惨,但是我们有没有想过用一个s数组,s[i]表示从1-i的a的和,s[i] = a[i] + s[i - 1]。想斐波那契数列一样,如下表:
),会TLE的很惨,但是我们有没有想过用一个s数组,s[i]表示从1-i的a的和,s[i] = a[i] + s[i - 1]。想斐波那契数列一样,如下表:
1 | 2 | 3 | 4 | 5 | |
a[] | 2 | 1 | 3 | 6 | 4 |
s[] | 2 | 3 | 6 | 12 | 16 |
这样l-r的和就是s[r] - s[l - 1]的值了,时间复杂度瞬间减少,变成O(2 * n)。
代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 10;
int a[N], s[N];
int n, m, r, l;
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
s[i] = a[i] + s[i - 1];
}
for(int i = 1; i <= m; i++)
{
cin >> l >> r;
cout << s[r] - s[l - 1] << endl;
}
return 0;
}到这里一维前缀和就已经讲完了,是不是觉得很简单,别急,难的来了——二维前缀和
二维前缀和
假设我们需要计算(x,y)的前缀和,如下图所示。

图中我们标注出三个点。
红色点表示(x,y)前缀和,用sum[x][y]表示。
蓝色表示(x,y-1)前缀和,用sum[x][y-1]表示。
黄色表示(x-1,y)前缀和,用sum[x-1][y]表示。
紫色表示(x-1,y-1)前缀和,用sum[x-1][y-1]表示。
假设第 i 行第 j 列对应的数组为,对应的二维前缀和为sum[i][j]。基于容斥原理,那么
sum[i][j] = sum[i - 1][j] + sum[i ][j - 1] - sum[i - 1][j - 1] + a[i][j]
代码如下,对应acwing796. 子矩阵的和
#include<bits/stdc++.h>
const int N = 1010;
int n, m, q;
int a[N][N], s[N][N];
int main()
{
scanf("%d%d%d", &n, &m, &q);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
scanf("%d", &a[i][j]);
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
s[i][j] = s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1] + a[i][j];
while (q--)
{
int x1, y1, x2, y2;
scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
printf("%d\n", s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
}
return 0;
}
到这里,你已经学会了前缀和。谢谢你的阅读,欢迎点赞收藏关注转发!

