AcWing1027. 方格取数

AcWing1027. 方格取数

设有 N×N 的方格图，我们在其中的某些方格中填入正整数，而其它的方格中则放入数字0。如下图所示：

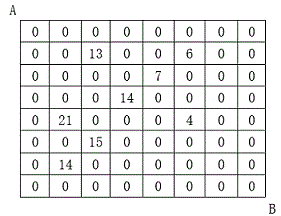
某人从图中的左上角 A 出发，可以向下行走，也可以向右行走，直到到达右下角的 B 点。

在走过的路上，他可以取走方格中的数（取走后的方格中将变为数字0）。

此人从 A 点到 B 点共走了两次，试找出两条这样的路径，使得取得的数字和为最大。

输入格式

第一行为一个整数N，表示 N×N 的方格图。

接下来的每行有三个整数，第一个为行号数，第二个为列号数，第三个为在该行、该列上所放的数。

行和列编号从 11 开始。

一行“0 0 0”表示结束。

输出格式

输出一个整数，表示两条路径上取得的最大的和。

数据范围

N≤10�≤10

输入样例：

8
2 3 13
2 6 6
3 5 7
4 4 14
5 2 21
5 6 4
6 3 15
7 2 14
0 0 0

输出样例：

67

难度：中等

时/空限制：1s / 64MB

总通过数：17424

总尝试数：25710

来源：《信息学奥赛一本通》 , NOIP2000提高组

算法标签 dp

---

k = i1 + j1 = i2 + j2 : 两个小朋友同时走, 每个人走的步数和是一样的.

f[i1, j1, i2, j2]​ : 由摘花生问题可以推广出从(1, 1), (1, 1)​​走到(i1, j1), (i2, j2)​能获得的最大花生数目.

由上面的两条性质可以推出三维的状态转移方程

f[i1,k−i1,i2,k−i2]→f[k,i1,i2]:两个小朋友同时走k步,从(1, 1), (1, 1)走到(i1, j1), (i2, j2)能获得的最大花生数目.

0:代表小朋友要到下边一个格子

1:代表小朋友要到右边一个格子

至此解决状态表示问题, 下面考虑集合划分

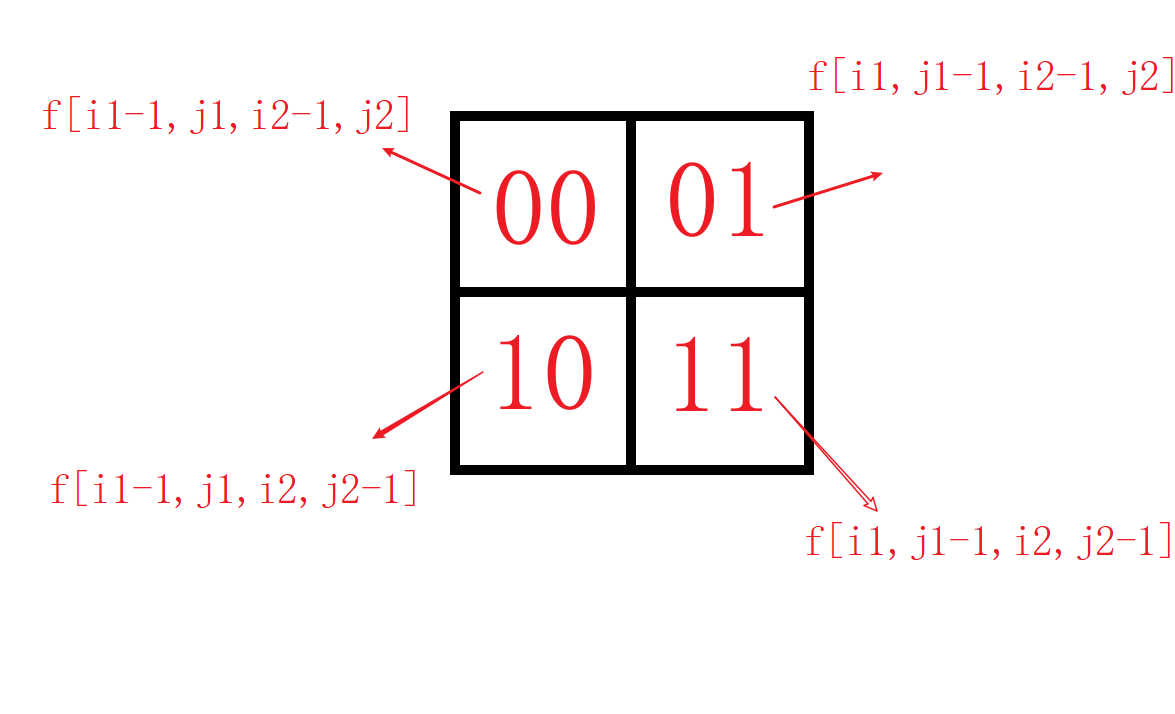
由于上面四种状态类似仅解释一个

f[i1−1,j1,i2−1,j2]→f[k−1,i1−1,i2−1]:代表两个小朋友都走了k−1步,小朋友1要从(i1−1,j1)

到(i1,j1),小朋友2要从(i2−1,j2)到(i2,j2).​

所以需要判断(i1,j1),(i2,j2)

是否是同一个格子,若是则仅需要加上一个权重,反之两个都需要

AC代码如下：

#include <bits/stdc++.h>
using namespace std;
const int N = 15;
int n;
int w[N][N];
int f[N * 2][N][N];
int main()
{
    scanf("%d", &n);
    int a, b, c;
    while (cin >> a >> b >> c, a || b || c) w[a][b] = c;
    for (int k = 2; k <= n + n; k ++ )
        for (int i1 = 1; i1 <= n; i1 ++ )
            for (int i2 = 1; i2 <= n; i2 ++ )
            {
                int j1 = k - i1, j2 = k - i2;
                if (j1 >= 1 && j1 <= n && j2 >= 1 && j2 <= n)
                {
                    int t = w[i1][j1];
                    if (i1 != i2) t += w[i2][j2];
                    int &x = f[k][i1][i2];
                    x = max(x, f[k - 1][i1 - 1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1 - 1][i2] + t);
                    x = max(x, f[k - 1][i1][i2 - 1] + t);
                    x = max(x, f[k - 1][i1][i2] + t);
                }
            }
    printf("%d\n", f[n + n][n][n]);
    return 0;
}