AcWing 1017. 怪盗基德的滑翔翼
怪盗基德是一个充满传奇色彩的怪盗,专门以珠宝为目标的超级盗窃犯。
而他最为突出的地方,就是他每次都能逃脱中村警部的重重围堵,而这也很大程度上是多亏了他随身携带的便于操作的滑翔翼。
有一天,怪盗基德像往常一样偷走了一颗珍贵的钻石,不料却被柯南小朋友识破了伪装,而他的滑翔翼的动力装置也被柯南踢出的足球破坏了。
不得已,怪盗基德只能操作受损的滑翔翼逃脱。
假设城市中一共有N幢建筑排成一条线,每幢建筑的高度各不相同。
初始时,怪盗基德可以在任何一幢建筑的顶端。
他可以选择一个方向逃跑,但是不能中途改变方向(因为中森警部会在后面追击)。
因为滑翔翼动力装置受损,他只能往下滑行(即:只能从较高的建筑滑翔到较低的建筑)。
他希望尽可能多地经过不同建筑的顶部,这样可以减缓下降时的冲击力,减少受伤的可能性。
请问,他最多可以经过多少幢不同建筑的顶部(包含初始时的建筑)?
输入格式
输入数据第一行是一个整数K,代表有K组测试数据。
每组测试数据包含两行:第一行是一个整数N,代表有N幢建筑。第二行包含N个不同的整数,每一个对应一幢建筑的高度h,按照建筑的排列顺序给出。
输出格式
对于每一组测试数据,输出一行,包含一个整数,代表怪盗基德最多可以经过的建筑数量。
数据范围
1≤K≤100,
1≤N≤100,
0<h<10000
输入样例:
3
8
300 207 155 299 298 170 158 65
8
65 158 170 298 299 155 207 300
10
2 1 3 4 5 6 7 8 9 10输出样例:
6
6
9首先,求一个高度递减的楼房子序列长度最大,其实就是求一个最长下降子序列
然后,这个怪盗基德老哥可以选择任意楼房作为起始位置,接着选择一个方向飞到尽头
于是,我们可以画出如下三种情况:
对于左边界情况来说,其实就是中间位置的左侧序列长度为 0 的情况;右边界情况同理
所以,我们只需讨论中间情况即可(两侧边界情况是该情况的子集)
于是,对于任意位置 x,我们分别需要求出以他为右端点的最长上升子序列,以及作为左端点的最长下降子序列
而DP中经典的最长上升子序列模型f[i]的状态表示就是以i为端点的最长上升子序列
由此我们通过线性DP,可以求出任一点的左侧最长上升和右侧最长下降
两者取一个 Max,就是以该点作为起点的最佳飞行方向的最大长度
然后再枚举所有点取一个 Max,就是最佳起点的最大长度,便是本题的答案
这题的DP模型就是经典的最长上升子序列
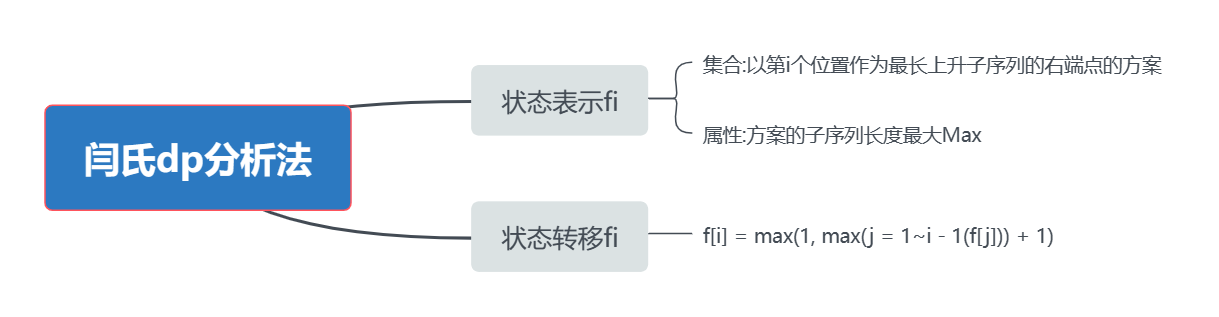
闫氏DP分析法
#include <bits/stdc++.h>
using namespace std;
const int N = 110;
int n;
int a[N], f[N];
int main()
{
int T;
scanf("%d", &T);
while(T--){
scanf("%d", &n);
for(int i = 1; i <= n; i++) scanf("%d", &a[i]);
int res = 0;
for(int i = 1; i <= n; i++){
f[i] = 1;
for(int j = 1; j < i; j++){
if(a[i] > a[j])
f[i] = max(f[i], f[j] + 1);
}
res = max(res, f[i]);
}
for(int i = n; i; i--){
f[i] = 1;
for(int j = n; j > i; j--)
if(a[i] > a[j])
f[i] = max(f[i], f[j] + 1);
res = max(res, f[i]);
}
printf("%d\n", res);
}
return 0;
}


【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 地球OL攻略 —— 某应届生求职总结
· 周边上新:园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源!
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】