回溯法解磁带最大利用率问题(python实现)
1、问题描述：设有n个程序{1，2，……，n}要存放在长度为L的磁带上。程序i存放在磁带上的长度是li(1<=i<=n)。程序存储问题要求确定这n个程序在磁带上的一个存储方案，使得能够在磁带上存储尽可能多的程序。在保证存储最多程序的前提下，还要求磁带的利用率达到最大。
2、算法设计：对于给定的n个程序存放在磁带上的长度，计算磁带上最多可以存储的程序数和占用磁带的长度。
3、数据输入：由文件input.txt给出输入数据。第1行是2个正整数，分别表示文件个数n和磁带的长度L。接下来的1行中，有n个正整数，表示程序存放在磁带上的长度。
4、结果输出：将计算的最多可以存储的程序数和占用磁带的长度及存放在磁带上的每个程序的长度输出到文件output.txt。第1行输出最多可以存储的程序数和占用磁带的长度；第2行输出存放在磁带上的每个程序的长度。
5、输入文件 input.txt示例：
9 50
2 3 13 8 80 20 21 22 23
输出文件output.txt示例：
5 49
2 3 13 8 23
6、实现思路：
用一棵子集树表示解空间。
贪心策略：最短程序优先。将程序从小到大排序，依次选取尽可能多的程序，但总长度不超过磁盘容量，则可求得最多可以存储的程序个数m。求得最多可以存储的程序个数m后，再求最大利用率。采用回溯法，从n个程序中选取总长度最大的m个，算法同装载问题（但此题m已知）。
7、代码：
# 4-12磁带最大利用率问题
xm = 0 #
n = 0 # 程序文件个数
L = 0 # 磁带总长度
len = [] # 程序在磁带上所占的长度
r = 0 # 剩余磁带的长度
cl = 0 # 当前占用磁带的长度(当前值)
bestl = 0 # 当前最大利用磁带时所占的长度(当前最优值)
x = [] # 当前路径(当前解)
bestx = [] # 当前最优路径(当前最优解)
def maxLoading(i, count): # 搜索第i层结点
global r
global xm
global cl
global bestl
if i >= n: # 到达叶节点
if xm == count:
for j in range(n):
bestx[j] = x[j]
bestl = cl
return
#搜索子树
r -= len[i]
if (cl + len[i] <= L) & (xm < count): # 搜索左子树
xm += 1
cl += len[i]
x[i] = 1
maxLoading(i+1, count)
cl -= len[i]
xm -= 1
if (cl + r) > bestl: # 搜索右子树
x[i] = 0
maxLoading(i+1, count)
r += len[i]
# 计算磁带最多可以存储的程序数
def greedy():
sum = 0
count = 0
for i in range(n):
sum += len[i]
if sum <= L:
count += 1
else:
break
return count
if __name__=="__main__":
xm = 0
cl = 0
bestl = 0
r = 0
strN = input("请输入程序文件个数n:")
strL = input("请输入磁带的长度L:")
n = int(strN)
L = int(strL)
bestx = [0 for _ in range(n)]
x = [0 for _ in range(n)]
strLen = input("请输入{}个程序需要的磁带长度(以空格分隔，以回车结束):".format(n))
len = strLen.split(" ")
len = list(map(int, len)) # str转为int
# len = [int(i) for i in len(len)]
for i in range(n):
r += len[i]
len.sort()
count = greedy()
print("最多可以存储的程序数：", count)
maxLoading(0, count) # 计算磁带的最优利用
print("磁带利用率最大时占用磁带的长度：", bestl)
print("程序时间从小到大排序结果：", len)
print("磁带利用率最大时的最优解：", bestx)
print("磁带利用率最大时存放在磁带上的每个程序的长度如下:")
for i in range(n):
if bestx[i] > 0: # bestx[i]=1
print(str(len[i]) + " ")
8、测试：
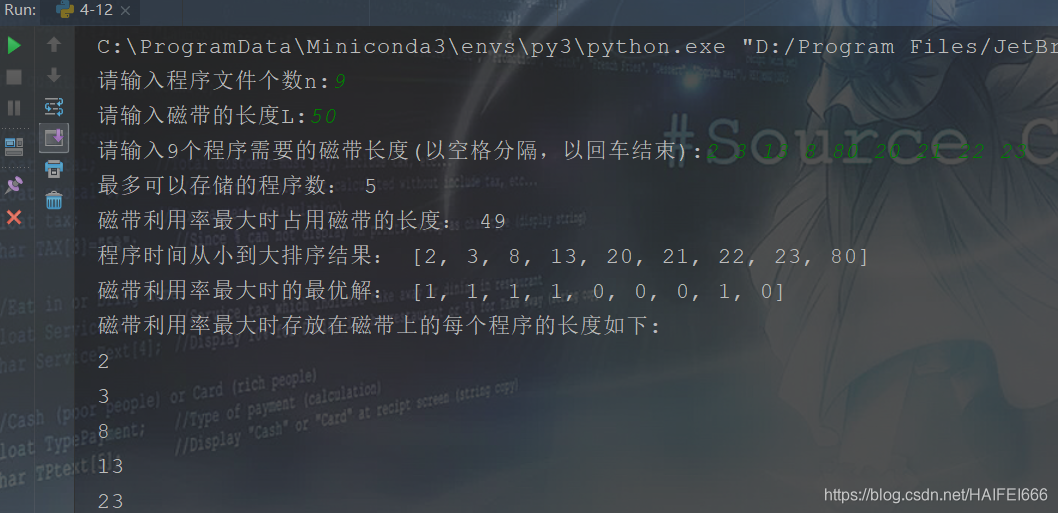
（1）输入：n=9，L=50，len=[2, 3, 13, 8, 80, 20, 21, 22, 23] ---> [2, 3, 8, 13, 20, 21, 22, 23, 80]
输出：count=5， bestl=49，bestx=[1, 1, 1, 1, 0, 0, 0, 1, 0] ---> 2,3,13,8,23
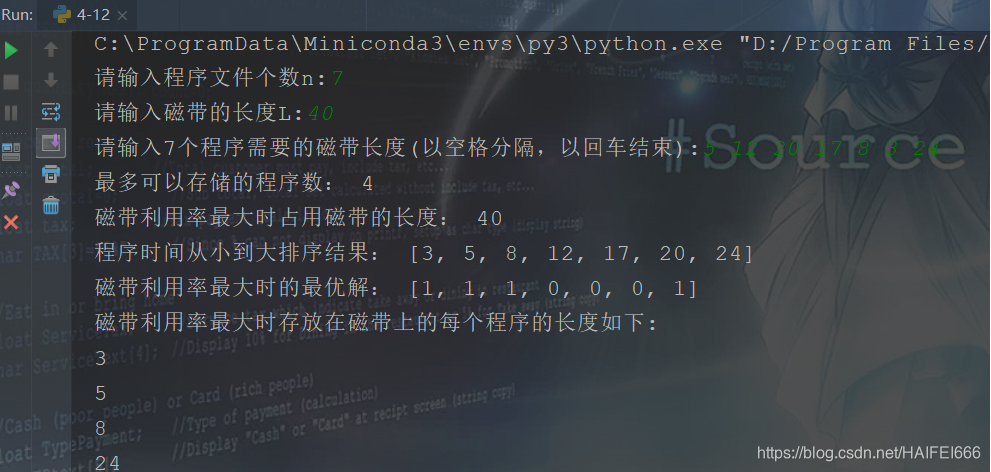
（2）输入：n=7，L=40，len=[5, 12, 20, 17, 8, 3, 24] ---> [3, 5, 8, 12, 17, 20, 24]
输出：count=5， bestl=49，bestx=[1, 1, 1, 0, 0, 0, 1] ---> 3,5,8,24
