【agc017E】Jigsaw
Description
给你\(n\)块积木,每块积木由三个矩形组成,中间的矩形最高高度为\(h\),左边的矩形高度为\(a_i\)离底边高度为\(c_i\),右边的矩形高度为\(b_i\)离底边高度为\(d_i\),现在要求将这些积木全部拼起来,并且中间部分的底边贴底,每个积木的左边和右边矩形的底边必须完全贴底或者完全贴在别的积木上,积木无法旋转或翻转,问是否存在合法的摆放方案
Solution
感觉。。emmm不是很好想反正我是想不到了
一开始有一个比较直接的想法,如果说积木\(i\)的\(c_i\)为\(0\),那么这个积木可以接在\(d_j=a_i\)的积木\(j\)的右边,类似的如果说积木\(i\)的\(d_i\)为\(0\),那么这个积木可以接在\(c_j=b_i\)的积木\(j\)的左边,然后我们可以考虑将这些积木连起来之类的就可以转化成一个图论问题
但实际上。。这并不是最好的转化方式
注意到\(h<=200\),实际上我们并不需要将积木看成点,我们可以将积木看成边,对于每一个高度建两个点(称为正点(\(P(x)\))和负点(\(N(x)\))),具体什么意思的话就是。。对于一个拼接处,属于右边的那块对应的是正点,属于左边的那块对应的是负点,具体高度的话就是拼接处的高度,这样讲比较不好理解的话。。举个例子:
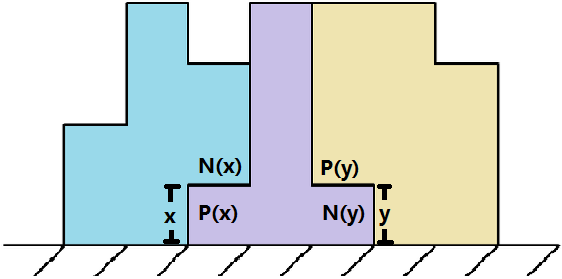
然后这样一来,连边的话就是对于每个积木,左边矩形对应的点向右边矩形对应的点连一条有向边,在上面这幅图来看的话就是\(P(x)\rightarrow N(y)\),那么现在我们的问题就变成了要在这个有向图中找若干条从正点开始在负点结束的路径,使得所有边都被经过一次(因为一条边对应一个积木)
这个时候有一个很机智的转化(这个时候应该疯狂orzdcx大神)
我们新搞一个超级源之类的点,如果说一个图存在一条这样的路径,那么我们从超级源向这条路径的起点连边,从终点再连一条有向边到超级源,那么我们可以得到一条回路,如果说整个图存在满足上述的“所有边都被经过一次”的划分,那么说明整个图(算上超级源)一定弱连通并且存在欧拉回路,具体构造的话就是。。每次从超级源出发走一条这样的路径回来,重复直到所有的边都经过了一次,这个时候将所有连着超级源的边都删掉就是一种合法的划分了
那么现在要做的就是判断是否存在欧拉回路了
一个弱连通图如果要存在欧拉回路,必须满足每个点的入度和出度相等,那么我们就首先可以得到两个限制条件:
(1)对于所有的正点,\(in[i]<=out[i]\)(之所以是\(<=\)是因为超级源会向路径起点连一条边,那么路径起点的入度会\(+1\),而我们的回路是放在整个包含超级源的图里面看的,所以是\(<=\))
(2)对于所有的负点,\(out[i]<=in[i]\)(类似地,终点要向超级源连边所以出度会要\(+1\))
有了这两个条件之后还有一个问题,就是我们并不能保证整个图连通,再具体一点就是我们会漏掉一个弱连通块满足这个弱连通块中的每一个点入度都和出度相等这种情况,这种情况没有办法通过起点终点与超级源连边的方式构造出欧拉回路(因为要求起点和终点一正一负,所以连了边之后起点和终点的出度和入度必定不相等),所以一旦出现这种情况肯定是无解的,否则的话就一定能按照上面说的构造方式构造出一种划分
代码大概长这个样子
#include<iostream>
#include<cstdio>
#include<cstring>
#define P(x) (x)
#define N(x) (x+h)
using namespace std;
const int N=1e5+10;
int f[N*2],outd[N*2],ind[N*2],ok[N*2];
int n,h;
int get_f(int x){return f[x]=f[x]==x?x:get_f(f[x]);}
void link(int x,int y){
get_f(x); get_f(y);
if (f[x]==f[y]) return;
f[f[y]]=f[x];
}
bool solve(){
for (int i=P(1);i<=P(h);++i)
if (ind[i]>outd[i]) return false;
for (int i=N(1);i<=N(h);++i)
if (ind[i]<outd[i]) return false;
for (int i=P(1);i<=N(h);++i)
if (ind[i]!=outd[i]) ok[get_f(i)]=1;
for (int i=P(1);i<=N(h);++i)
if (!ok[get_f(i)]&&(ind[i]||outd[i])) return false;
return true;
}
int main(){
#ifndef ONLINE_JUDGE
freopen("a.in","r",stdin);
#endif
int a,b,c,d;
int l,r;
scanf("%d%d",&n,&h);
for (int i=P(1);i<=N(h);++i) f[i]=i,ind[i]=outd[i]=0,ok[i]=0;
for (int i=1;i<=n;++i){
scanf("%d%d%d%d",&a,&b,&c,&d);
l=c?N(c):P(a);
r=d?P(d):N(b);
link(l,r);
++outd[l]; ++ind[r];
}
if (solve()) printf("YES\n");
else printf("NO\n");
}


