【bzoj3230】相似子串
Description
给你一个长度为\(n\)的字符串,把它的所有本质不同的子串按字典序大小排序,有\(m\)个询问,对于每一个询问\(x,y\)你需要回答排名\(x\)和子串和排名\(y\)的子串的最长公共前缀的平方和+最长公共后缀的平方和,如果询问不合法输出\(-1\)
数据范围:\(n<=10^5,m<=10^5\),字符串只含有小写字母
Solution
虽然说貌似是。。后缀数组的裸题。。
但是场上没有写出来。。所以还是拎出来智力康复。。
假设我们已经求出来\(sa\)数组和\(height\)数组,怎么来做这个题呢
首先需要判断询问合不合法,即要求出本质不同的子串的个数
这里可以直接用\(height\)数组求解,以样例为例子,放个图就比较好理解了:
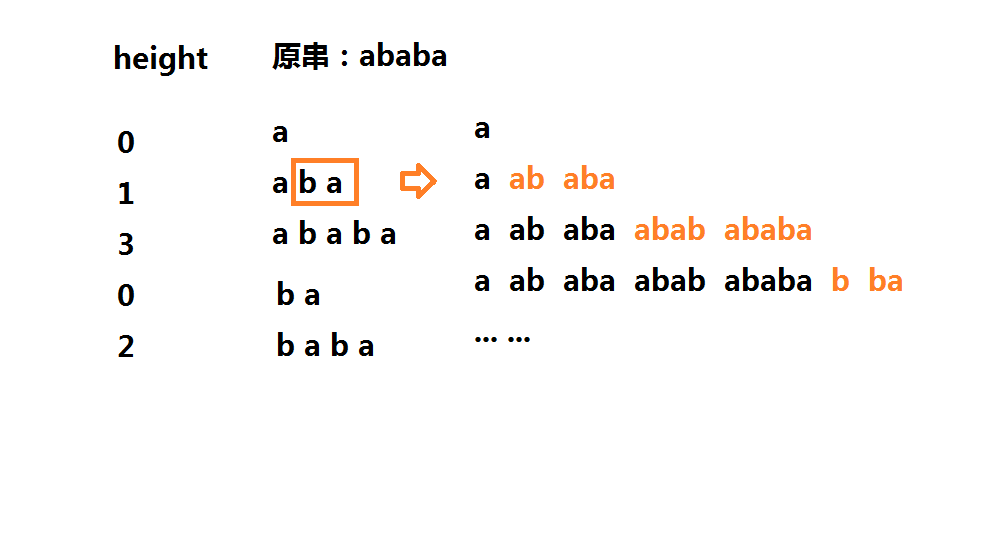
简单一点来说就是非公共前缀的部分才能贡献新的本质不同的子串
所以我们稍微减一下就能够知道每一个后缀贡献了几个新的子串了,前缀和一下,把这个存前缀和的数组记为\(num\),则\(num[i]\)表示排名为\(1\)到\(i\)的后缀总共贡献了几个子串
那么总的本质不同的子串的数量就是\(num[n]\)了
接下来就是求最长公共前缀
如果知道了两个子串具体是啥当然很好做啦,只要子串的开头对应的两个后缀RMQ一下然后跟两个子串的长度取个\(min\)就好了
然而这里的主要问题出在我们要定位,但是因为我们有了\(num\)数组,所以直接二分一下就可以知道是由哪个后缀产生的了(找到第一个\(num\)大于等于的即可)
最后是后缀
后缀的话其实就是反串的前缀,处理方式相同,但是定位的话我们可以直接根据求最长公共前缀的时候定位得到的信息,反转一下就能知道在反串中是由哪个后缀产生的了
最后的话是。。输出的时候和子串数量的统计都需要long long
代码大概长这个样子
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#define ll long long
#define TOP 20
using namespace std;
const int N=100010;
char s[N];
int n,m,lens;
struct Sa{/*{{{*/
int a[N],b[N],c[N];
int rk[N],height[N],sa[N],mn[N][TOP+1];
ll num[N];
int mx,n;
bool cmp(int x,int y,int len,int *r)
{return r[x]==r[y]&&r[x+len]==r[y+len];}
void sort(int n){
for (int i=0;i<=mx;++i) c[i]=0;
for (int i=1;i<=n;++i) ++c[a[b[i]]];
for (int i=1;i<=mx;++i) c[i]+=c[i-1];
for (int i=n;i>=1;--i) sa[c[a[b[i]]]--]=b[i];
}
void get_sa(int _n){
mx=0; n=_n;
for (int i=1;i<=n;++i) b[i]=i,a[i]=s[i]-'a'+1,mx=max(mx,a[i]);
int cnt=0;
sort(n);
for (int len=1;cnt<n;len*=2){
cnt=0;
for (int i=n-len+1;i<=n;++i) b[++cnt]=i;
for (int i=1;i<=n;++i)
if (sa[i]>len)
b[++cnt]=sa[i]-len;
sort(n);
swap(a,b);
cnt=1;
a[sa[1]]=1;
for (int i=2;i<=n;a[sa[i++]]=cnt)
if (!cmp(sa[i],sa[i-1],len,b))
++cnt;
mx=cnt;
}
}
void get_height(){
for (int i=1;i<=n;++i) rk[sa[i]]=i;
int k=0;
for (int i=1;i<=n;++i){
if (k>0) --k;
while (s[i+k]==s[sa[rk[i]-1]+k]) ++k;
height[rk[i]]=k;
}
cnt_num();
rmq();
}
void cnt_num(){
for (int i=1;i<=n;++i)
num[i]=num[i-1]+(n-sa[i]+1-height[i]);
}
void rmq(){
for (int i=1;i<=n;++i) mn[i][0]=height[i];
for (int j=1;j<=TOP;++j)
for (int i=n-(1<<j)+1;i>=1;--i)
mn[i][j]=min(mn[i][j-1],mn[i+(1<<j-1)][j-1]);
}
int lcp(int x,int y){//x&y are ranks
if (x==y) return n-sa[x]+1;
if (x>y) swap(x,y);
++x;
int tmp=(int)(log(1.0*(y-x+1))/log(2.0));
return min(mn[x][tmp],mn[y-(1<<tmp)+1][tmp]);
}
int query(ll x,ll y,int &edx,int &edy,int &lenx,int &leny){
int posx,posy;
posx=lower_bound(num+1,num+1+n,x)-num;
posy=lower_bound(num+1,num+1+n,y)-num;
int ret=lcp(posx,posy);
lenx=n-sa[posx]+1-(num[posx]-x);
leny=n-sa[posy]+1-(num[posy]-y);
edx=n-sa[posx]+1-lenx+1;
edy=n-sa[posy]+1-leny+1;
return min(ret,min(lenx,leny));
}
int query2(int stx,int sty,int lenx,int leny){
int ret=lcp(rk[stx],rk[sty]);
return min(ret,min(lenx,leny));
}
}a[2];/*}}}*/
int main(){
#ifndef ONLINE_JUDGE
freopen("a.in","r",stdin);
#endif
int tmp1,tmp2,edx,edy,lenx,leny;
ll x,y;
scanf("%d%d",&n,&m);
scanf("%s",s+1);
lens=strlen(s+1);
a[0].get_sa(lens); a[0].get_height();
for (int i=1;lens-i+1>i;++i) swap(s[i],s[lens-i+1]);
a[1].get_sa(lens); a[1].get_height();
for (int i=1;i<=m;++i){
scanf("%lld%lld",&x,&y);
if (x>a[0].num[n]||y>a[0].num[n]) printf("-1\n");
else{
tmp1=a[0].query(x,y,edx,edy,lenx,leny);
tmp2=a[1].query2(edx,edy,lenx,leny);
printf("%lld\n",1LL*tmp1*tmp1+1LL*tmp2*tmp2);
}
}
}

