【learning】多项式乘法&fft
[吐槽]
以前一直觉得这个东西十分高端完全不会qwq
但是向lyy、yxq、yww、dtz等dalao们学习之后发现这个东西的代码实现其实极其简洁
于是趁着还没有忘记赶紧来写一篇博
(说起来这篇东西的文字好像有点多呀qwq啊话痨是真的qwq)
[正题]
一些预备知识(有了解的就可以直接跳啦,mainly from 算导)
fft的话,用来解决与多项式乘法有关的问题
关于多项式
一个以x为变量的多项式定义在一个代数域$F$上,将函数$A(x)$表示为形式和:
$A(x) = \sum\limits_{i=0}^{n-1} a_ix^i$
显然该多项式有$n$项,我们称 $a_0, a_1, a_2 ... a_{n-1}$ 为该多项式的系数
如果说一个多项式$A(x)$的最高次的非零系数是$a_k$,那么称$A(x)$的次数是$k$
任何严格大于一个多项式次数的整数都是该多项式的次数界
那么显然,我们可以用一个$n$次多项式的$n$个系数来表示这个多项式
在多项式上定义的运算
对于加法,就是直接对应系数相加就好了
对于乘法,
如果说$A(x)$ 和 $B(x)$ 皆是次数为$n$的多项式,则它们的乘积$C(x)$ 是一个次数界为$2n-1$的多项式
对于所有属于定义域的$x$,都有$C(x)=A(x)*B(x)$
那么如何快速求两个多项式的乘积呢?
我们知道对于一个$n$次多项式,知道了其函数图像上的$n$个点之后,就能将这个多项式确定下来了
所以就考虑通过计算求出到$C(x)$函数图像上的$2n-1$个点,从而确定$C(x)$
那么如何用一种高效的方式解决这个问题呢?就是接下来要讲的东西啦
总的来说. . . 我们要干什么?
显然,我们现在要寻找一种快速的方法来求两个多项式的乘积
接下来介绍的方法思路就是上面提到的:先求出点值,再确定多项式
根据乘积$C(x)$满足的性质,我们可以取$2n-1$个不同的$x1$,将$A(x1)$和$B(x1)$分别算出来
然后再用两者相乘得到这个位置的$C(x1)$
直接算效率是极低的,但是如果说我们选择的点有一些特殊性质呢?
如果说我们选择的位置满足某种性质,使得我们在计算系数的时候能够省掉一些步骤
(比如说系数中满足某种关系啊之类的)
那么我们的效率就会相对来说高一些了
接下来介绍的方法,用到一个叫做DFT的东西(说白了就是选择一些特殊的点),通过求两个多项式的系数向量的DFT,得到确定$C(x)$所需要的点值,然后再通过其逆运算,得到$C(x)$
这就是接下来的内容的大概思路
特殊的点?单位复数根
(在下文的叙述中用$i$来表示$-1$的平方根)
$n$次单位复数根是满足$\omega^n=1$的复数$\omega$
$n$次单位复数根恰好有$n$个,对于$k=0, 1, ... , n-1$,这些根是$e^{2\pi ik/n}$
对于这个表达式的计算,我们可以利用复数的指数形式的定义:
$e^{iu} = cos(u) + i sin(u)$
我们考虑将一个复数在坐标系上用一个点来表示
对于一个复数$x$,我们可以将其表示为这种形式:
$x = a+b*i $ $(a,b\in R)$
考虑这样的一个坐标系,其横轴为实数轴,纵轴为虚数轴
那么我们可以将$x$这个数表示为该坐标系(其实就是复平面)中的点$(a,b)$
那么将$n$个$n$次单位复数根画出来的话(以$n=8$为例),大概是长这样:
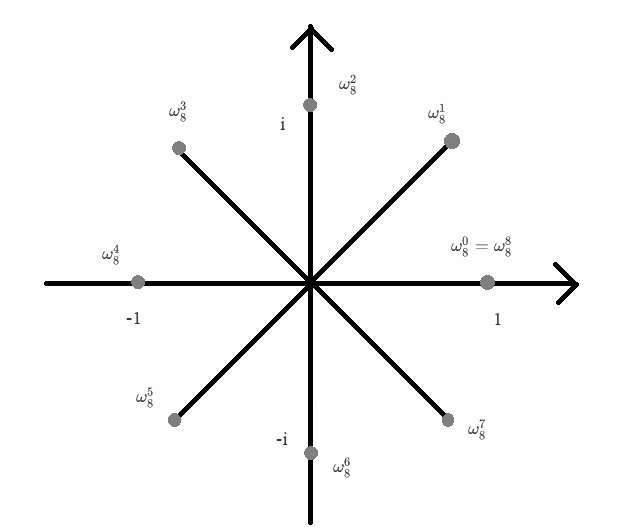
其实如果画得足够标准,这个些单位复数根应该分布在一个以原点为圆心的圆上。。。
(这个好像一点都不像一个圆啊喂qwq)
(嗯好像这点在接下来的讲述中并不会用到,不过码上来总是好的ovo)
那么接下来给出一些关于$n$次单位复数根的基本性质
(注意这也是后面FFT之所以能在O(nlogn)时间内求得的重要原因)
消去引理(好像有点像。。约分?哈哈哈)
对任何整数$n >= 0, k >=0, $以及$d > 0$,有
$\omega_{dn}^{dk} = \omega_{n}^{k}$
证明就直接将其定义带进去就好:$\omega_{dn}^{dk} = (e^{2\pi i/dn})^{dk} = (e^{2\pi i/n})^k = \omega_n^k$
那么由这条式子我们可以得到一个推论:
$\omega_{n}^{n/2} = \omega_2 = -1$
折半引理
如果 $n>0$ 为偶数,那么 $n$ 个 $n$ 次单位复数根的平方的集合就是 $n/2$ 个 $n/2$ 次单位复数根的集合
证明的话:
首先,根据消去引理,对于任意的非负整数 $k$ ,有
$(\omega_{n}^{k})^2 = \omega_{n/2}^{k}$
然后我们会发现,如果对于所有的$n$次单位复数根平方,会得到每个$n/2$次单位根正好2次,因为
$(\omega_{n}^{k+n/2})^2 = \omega_{n}^{2k+n} = \omega_{n}^{2k} * \omega_{n}^{n} = \omega_{n}^{2k} = (\omega_{n}^{k})^2$
所以还可以得到这样一条式子
$(\omega_{n}^{k+n/2} )^2= (\omega_{n}^{k})^2 $
求和引理
对任意整数$n>=1$ 和不能被$n$整除的非负整数$k$,有
$\sum\limits_{i=0}^{n-1} (\omega_{n}^{k})^i = 0$
证明:
$\sum\limits_{i=0}^{n-1} (\omega_{n}^{k})^i = \frac{(\omega_{n}^{k})^n-1}{\omega_{n}^{k}-1} = \frac{(\omega_{n}^{n})^k-1}{\omega_{n}^{k}-1} = \frac{(1)^k-1}{\omega_{n}^{k}-1} =0$
于是乎我们开始真正步入正题来求……
DFT
在介绍完什么是单位复数根之后,就可以引入DFT的概念了
计算一个次数界为$n$的多项式 :
$A(x) = \sum\limits_{i=0}^{n-1} a_i x_i$
在$\omega_{n}^{0},\omega_{n}^{1} ... \omega_{n}^{n-1}$处的取值(也就是在$n$个$n$次单位复数根处),
定义其结果$y_k$:
$y_k = A(\omega_n^k)$
向量$y$就是系数向量 $a = (a_0, a_1, a_2 ,..., a_{n-1})$(也就是A的系数)的DFT(离散傅里叶变换)
我们记为$y=DFT_n(a)$
FFT
嗯?名字是不是和上面长得很像啊?
原因是因为,FFT其实就是快速求DFT,叫做快速傅里叶变换
利用复数单位根的特殊性质,我们就可以在$O(nlogn)$时间内算出$DFT_n(a)$
接下来就是算法部分啦
一些必须先约定的东西:接下来的内容中$n$都恰好是2的整数幂
(如果说实际处理中出现次数界不是2的整数幂呢?强行补成就好啦,不存在的那些项系数=0即可)
我们考虑分治策略,根据$A(x)$中系数下标的奇偶性分成两组,变成两个新的次数界为$n/2$的多项式
这里分别定义两个新的多项式:
$A_0(x) = a_0 + a_2x + a_4x^2 + ... +a_{n-2}x^{n/2-1}$
$A_1(x) = a_1 + a_3x + a_5x^2 + ... +a_{n-1}x^{n/2-1}$
($A_0(x)$中包含了$A$中所有下标为偶数的系数,$A_1(x)$中包含了所有下标为奇数的系数)
那么显然有:
$A(x) = A_0(x^2) + x*A_1(x^2)$
至此,发现我们的问题直接就转化为了:
求次数界为$n/2$的多项式$A_0(x)$和$A_1(x)$在点$(\omega_n^0)^2 , (\omega_n^1)^2 , ... , (\omega_n^{n-1})^2$的取值
于是乎这样好像就把我们原来的问题成功拆成了两个形式与原问题相同的子问题
假设我们现在已经求得了$A_0(\omega_{n/2}^k)$和$A_1(\omega_{n/2}^k)$
如何得到由它们快速得到$A$中的系数呢?
这时候就要用到单位复数根的奇妙性质啦
根据消去引理,有$\omega_{n/2}^k = \omega_{n}^{2k}$
于是
$A_0(\omega_{n/2}^k) = A_0(\omega_{n}^{2k})$
$A_1(\omega_{n/2}^k) = A_1(\omega_{n}^{2k})$
这个时候我们用表达$A_0(x)$和$A_1(x)$与$A(x)$之间的关系的那条式子推一下,会发现
$A_0(\omega_{n}^{2k}) + \omega_{n}^{k} * A_1(\omega_{n}^{2k}) = A(\omega_{n}^{k})$
稍微绕一下弯,还可以得到这样的一条式子
$A_0(\omega_{n}^{2k}) - \omega_{n}^{k} * A_1(\omega_{n}^{2k}) = A(\omega_{n}^{k+n/2})$
为什么呢?
一步步来的话是这样的:
首先,我们知道$\omega_{n}^{n/2} = \omega_2 = -1$ (消去引理的推论)
然后有:
$ - \omega_n^k = -1 * \omega_n^k = \omega_{n}^{n/2} * \omega_n^k = \omega_{n}^{k+n/2}$
所以第二条式子其实是等于
$A_0(\omega_{n}^{2k}) + \omega_{n}^{k+n/2} * A_1(\omega_{n}^{2k})$
然后根据折半引理,我们可以知道$\omega_n^{2k+n} = \omega_n^{2k}$
所以上面的式子又等于
$A_0(\omega_{n}^{2k+n}) + \omega_{n}^{k+n/2} * A_1(\omega_{n}^{2k+n}) $
然后我们会发现这其实就是一个$A_0(x) + x * A_1(x) $的形式
这样这条式子最终就等于$A(\omega_{n}^{k+n/2})$啦
总结一下,如果说我们得到了$A_0(\omega_{n/2}^{k})$(记为$y_0$)以及$A_1(\omega_{n/2}^{k})$(记为$y_1$)
那么我们就可以得到$A(\omega_{n}^{k})$以及$A(\omega_{n}^{k+n/2})$了
其中
$A(\omega_{n}^{k}) = y_0 + y_1$
$A(\omega_{n}^{k+n/2}) = y_0 - y_1$
至此,我们就完成了将原来的问题拆成了两个规模为一半的问题的求解
就可以在$O(nlogn)$的时间内求出DFT啦
递归版的代码如下(这里是非完整的代码,完整版会在后面给出)
1 struct cmplx 2 { 3 double a,b;//a记录这个复数的实数部分,b记录这个复数的i的系数 4 cmplx(){} 5 cmplx(double x,double y){a=x,b=y;} 6 friend cmplx operator + (cmplx x,cmplx y) 7 {return cmplx(x.a+y.a,x.b+y.b);} 8 friend cmplx operator - (cmplx x,cmplx y) 9 {return cmplx(x.a-y.a,x.b-y.b);} 10 friend cmplx operator * (cmplx x,cmplx y) 11 {return cmplx(x.a*y.a-x.b*y.b,x.a*y.b+x.b*y.a);} 12 }; 13 typedef vector<cmplx> vc 14 15 vc fft(vc ans) 16 { 17 int n=ans.size(); 18 if (n==1) return ans; 19 cmplx w_n=cmplx(cos(2*pi/n),sin(2*pi/n)),w=cmplx(1,0); 20 vc a0,a1; 21 for (int i=0;i<n;i+=2) 22 a0.push_back(ans[i]),a1.push_back(ans[i+1]); 23 //得到A0和A1 24 25 a0=fft(a0,op); 26 a1=fft(a1,op); 27 //递归求出将单位复数根带入得到的值 28 29 for (int i=0;i<(n>>1);++i) 30 { 31 ans[i]=a0[i]+a1[i]*w; 32 ans[i+(n>>1)]=a0[i]-a1[i]*w; 33 w=w*w_n; 34 //利用得到的关系式由A0和A1推得A 35 } 36 return ans; 37 }
所以说...我们要怎么求回来?
现在我们已经成功滴把DFT搞出来了,也就可以求得我们所需要的用来确定$C(x)$的点值了,剩下的工作就是插值啦
插值的方法有很多,这里考虑将DFT写成一个矩阵方程 $y = V_n a$
其中向量$y$表示的是DFT,向量$a$为原多项式的系数
$V_n$是一个由$\omega_n$适当幂次填充成的范德蒙德矩阵
那么现在问题来了:
范德蒙德矩阵又是什么高端玩意?!
其实这个东西大概长这样:
\begin{bmatrix}
1&x_0&x_0^2&...&x_0^{n-1}\\
1&x_1&x_1^2&...&x_1^{n-1}\\
1&...&...&...&...\\
1&x_{n-1}&x_{n-1}^2&...&x_{n-1}^{n-1}
\end{bmatrix}
所以如果说我们想要由$y$得到$a$,只需要乘上逆矩阵$V_n^{-1}$就好了
($V_n^{-1} * V_n = $单位矩阵)
考虑逆矩阵中的元素的特点
然后根据求和引理(中间的过程有点。。看算导的话好像会更加清晰一些),可以得出这样的结论:
$a_i = \frac{1}{n} \sum\limits_{k=0}^{n-1} y_k \omega_n^{-kj}$
说得简单一点就是,
由DFT反过来求原来的系数只要用$\omega_n^{-1}$替换掉$\omega_n$,并在最后将每个元素除以$n$就好啦
实现的话,会发现其实与DFT的区别仅仅在于一个负号,其他部分的代码实现是完全一样的
(爽到了爽到了哈哈哈qwq)
所以说其实完全可以在调用函数的时候多带一个参数,表示是否是求$DFT^-1$,这样就十分方便滴将两个函数合并成一个啦
最后在这里附上递归版完整的代码(求的是两个多项式$a$和$b$的乘积)

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #define ll long long 6 using namespace std; 7 const double pi=acos(-1); 8 const int MAXN=(1<<17)+10; 9 struct cmplx 10 { 11 double a,b;//a记录这个复数的实数部分,b记录这个复数的i的系数 12 cmplx(){} 13 cmplx(double x,double y){a=x,b=y;} 14 friend cmplx operator + (cmplx x,cmplx y) 15 {return cmplx(x.a+y.a,x.b+y.b);} 16 friend cmplx operator - (cmplx x,cmplx y) 17 {return cmplx(x.a-y.a,x.b-y.b);} 18 friend cmplx operator * (cmplx x,cmplx y) 19 {return cmplx(x.a*y.a-x.b*y.b,x.a*y.b+x.b*y.a);} 20 }a[MAXN],b[MAXN]; 21 int n,m,k; 22 int fft(cmplx *ans,int n,int op); 23 24 int main() 25 { 26 // freopen("a.in","r",stdin); 27 // freopen("a.out","w",stdout); 28 29 int type; 30 scanf("%d%d%d",&n,&m,&type); 31 for (int i=0;i<=n;++i) scanf("%lf",&a[i].a); 32 for (int i=0;i<=m;++i) scanf("%lf",&b[i].a); 33 k=1; 34 while (k<n+m) k<<=1; 35 fft(a,k,1); 36 fft(b,k,1); 37 for (int i=0;i<=k;++i) a[i]=a[i]*b[i]; 38 fft(a,k,-1); 39 for (int i=0;i<=n+m;++i) 40 printf("%lld ",(ll)(a[i].a/k+0.5));//最后一定要记得除 41 } 42 43 int fft(cmplx *ans,int n,int op) 44 { 45 if (n==0) return 0; 46 cmplx a0[n>>1],a1[n>>1],w_n=cmplx(cos(2*pi/n),op*sin(2*pi/n)),w=cmplx(1,0); 47 //注意在求逆DFT的时候,也就是在w_n的i的系数那里多了一个负号罢了 48 for (int i=0;i<=n;i+=2) 49 a0[i>>1]=ans[i],a1[i>>1]=ans[i+1]; 50 fft(a0,n>>1,op); 51 fft(a1,n>>1,op); 52 for (int i=0;i<(n>>1);++i) 53 { 54 ans[i]=a0[i]+a1[i]*w; 55 ans[i+(n>>1)]=a0[i]-a1[i]*w; 56 w=w*w_n; 57 } 58 }
然后其实还有一种非递归的写法,常数会小很多,写起来也是十分的简洁
但是因为里面的一些操作的需要用到一些关于二进制的知识讲述清楚可能还是需要一定的篇幅
而这篇东西的篇幅本来就够长的了。。所以说就先挖个坑贴上代码,具体就留在下一篇再讲吧qwq
(随处挖坑 然后不填 系列)

1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<cmath> 5 #include<vector> 6 #define ll long long 7 using namespace std; 8 const double pi=acos(-1); 9 const int MAXN=(1<<17)+10; 10 struct cmplx 11 { 12 double a,b; 13 cmplx(){} 14 cmplx(double x,double y){a=x,b=y;} 15 friend cmplx operator + (cmplx x,cmplx y) 16 {return cmplx(x.a+y.a,x.b+y.b);} 17 friend cmplx operator - (cmplx x,cmplx y) 18 {return cmplx(x.a-y.a,x.b-y.b);} 19 friend cmplx operator * (cmplx x,cmplx y) 20 {return cmplx(x.a*y.a-x.b*y.b,x.a*y.b+x.b*y.a);} 21 }a[MAXN],b[MAXN],ans[MAXN]; 22 int rev[MAXN]; 23 int n,m,k,lg; 24 //vc fft(vc ans,int op); 25 int fft(cmplx *a,int op); 26 int get_rev(cmplx *a,int n); 27 28 int main() 29 { 30 // freopen("a.in","r",stdin); 31 // freopen("a.out","w",stdout); 32 33 int type,x; 34 scanf("%d%d%d",&n,&m,&type); 35 ++n,++m; 36 for (int i=0;i<n;++i) scanf("%lf",&a[i].a); 37 for (int i=0;i<m;++i) scanf("%lf",&b[i].a); 38 k=1; 39 while (k<n+m) k<<=1; 40 fft(a,1); 41 fft(b,1); 42 for (int i=0;i<k;++i) a[i]=a[i]*b[i]; 43 fft(a,-1); 44 for (int i=0;i<n+m-1;++i) 45 printf("%lld ",(ll)(a[i].a/k+0.5)); 46 } 47 48 int fft(cmplx *a,int op) 49 { 50 int step,bit=0; 51 cmplx w_n,w,t,u; 52 for (int i=1;i<k;i<<=1,++bit); 53 rev[0]=0; 54 for (int i=0;i<k;++i) rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1)); 55 for (int i=0;i<k;++i) 56 if (i<rev[i]) swap(a[i],a[rev[i]]); 57 //简单说一下:就是因为我们会发现其实递归到最下层的顺序是可以确定的 58 //然后就可以通过奇妙的方式(用到有关二进制的东西)得到这个顺序,然后就直接模拟向上更新的过程就好啦 59 for (int step=2;step<=k;step<<=1) 60 { 61 w_n=cmplx(cos(2*pi/step),op*sin(2*pi/step)); 62 for (int st=0;st<k;st+=step) 63 { 64 w=cmplx(1,0); 65 for (int i=0;i<(step>>1);++i) 66 { 67 t=a[st+i+(step>>1)]*w; 68 u=a[st+i]; 69 a[st+i]=u+t; 70 a[st+i+(step>>1)]=u-t; 71 w=w*w_n; 72 } 73 } 74 } 75 }
[总结]
其实fft这个东西仔细想想还是很有意思的(特别是代码的简洁哈哈)
难得更了一篇这么长的博,希望对这方面的理解能够有所帮助吧ovo



