最大子段和 问题总结
2013-11-03 18:59 youxin 阅读(1842) 评论(0) 编辑 收藏 举报一维数组: 有n个数(以下都视为整数),每个数有正有负,现在要在n个数中选取相邻的一段,使其和最大,输出最大的和。
[a1,a2,a3................,an].
解法1:很自然的想法
int maxSum1(int a[],int n,int &besti,int &bestj) { int sum=0; for(int i=1;i<=n;i++) { for(int j=i;j<=n;j++) { int thissum=0; for(int k=i;k<=j;k++) thissum+=a[k]; if(thissum>sum) { sum=thissum; besti=i; bestj=j; } } } return sum; }
解法2:
我们可以将后面的一个for循环去掉:
int maxSum2(int a[],int n,int &besti,int &bestj) { int sum=0; for(int i=1;i<=n;i++) { int thissum=0; for(int j=i;j<=n;j++) { thissum+=a[j]; if(thissum>sum) { sum=thissum; besti=i; bestj=j; } } } return sum; }
解法3:分治算法:

int maxSubSum(int a[],int left,int right) { int sum=0; if(left==right) sum=a[left]>0?a[left]:0; else { int center=(left+right)/2; int leftSum=maxSubSum(a,left,center); int rightSum=maxSubSum(a,center+1,right); int s1=0; int lefts=0; for(int i=center;i>=left;i--) { lefts +=a[i]; if(lefts>s1) s1=lefts; } int s2=0; int rights=0; for(int i=center+1;i<=right;i++) { rights +=a[i]; if(rights>s2) s2=rights; } sum=s1+s2; if(sum<leftSum) sum=leftSum; if(sum<rightSum) sum=rightSum; } return sum; } int maxSum3(int a[],int n) { return maxSubSum(a,1,n); }
解法4:动态规划

上面公式看不清楚,可以看下面的:
记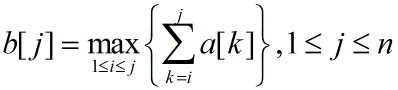 ,则所求的最大子段和为:
,则所求的最大子段和为:
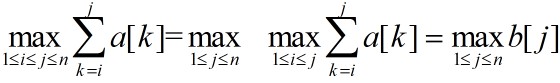
由b[j]的定义知,当b[j-1]>0时,b[j]=b[j-1]+a[j],否则b[j]=a[j]。由此可得b[j]的动态规划递推式如下:
b[j]=max{b[j-1]+a[j],a[j]},1<=j<=n。
int maxSum4(int a[],int n) { int sum=0; int b=0; for(int i=1;i<=n;i++) { if(b>0) b+=a[i]; else b=a[i]; if(b>sum) sum=b; } return sum; }
动态规划解释:
——动态规划。我们令一个数组f,f[i]表示前i个元素能组成的最大和。如果f[i-1]大于零,则不管a[i]的情况,f[i-1]都可以向正方向影响a[i],因此可以将a[i]加在f[i-1]上。如果f[i-1]小于零,则不管a[i]再大,都会产生负影响,因此我们还不如直接令f[i]=a[i]。因此状态转移方程就在这里。我们只需在f中扫描一次,找到最大的值就是最大子段的和。
int LSS_DP(int a[]) //求最大子段和,动态规划,O(n)
{
int f[101], n = a[0], max = -200000000; //f[i]表示第 i 个数能构成的最大和, max 表示当前所有中的最大和
f[1] = a[1];
for (int i = 2; i <= n; i++)
{
if (f[i - 1] > 0) //如果第 i 个数后面一个数能构成的最大子段和大于 0
{
f[i] = f[i - 1] + a[i]; //大于就将第 i 个数加入其中
}
else
f[i] = a[i]; //否则第 i 个数自己组成一个最大子序列
if (f[i] > max) //更新最大值
max = f[i];
}
return max;
}
还可以扩展该问题。
最大m子段和问题
(1)问题描述:给定由n个整数(可能为负数)组成的序列a1,a2,a3……an,以及一个正整数m,要求确定此序列的m个不相交子段的总和达到最大。最大子段和问题是最大m字段和问题当m=1时的特殊情形。
(2)问题分析:设b(i,j)表示数组a的前j项中i个子段和的最大值,且第i个子段含a[j](1<=i<=m,i<=j<=n),则所求的最优值显然为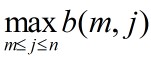 。与最大子段问题相似,计算b(i,j)的递归式为:
。与最大子段问题相似,计算b(i,j)的递归式为: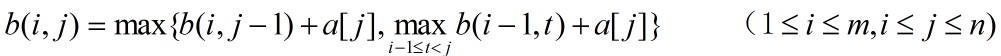
其中,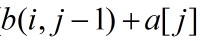 表示第i个子段含a[j-1],而
表示第i个子段含a[j-1],而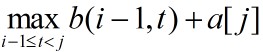 项表示第i个子段仅含a[j]。初始时,b(0,j)=0,(1<=j<=n);b(i,0)=0,(1<=i<=m)。
项表示第i个子段仅含a[j]。初始时,b(0,j)=0,(1<=j<=n);b(i,0)=0,(1<=i<=m)。
更多:
http://blog.csdn.net/liufeng_king/article/details/8632430





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 基于Microsoft.Extensions.AI核心库实现RAG应用
· Linux系列:如何用heaptrack跟踪.NET程序的非托管内存泄露
· 开发者必知的日志记录最佳实践
· SQL Server 2025 AI相关能力初探
· Linux系列:如何用 C#调用 C方法造成内存泄露
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通