水塘抽样问题

2013-10-01 04:18 youxin 阅读(6031) 评论(0) 编辑收藏举报

google曾经有一道面试题，十分有趣：

I have a linked list of numbers of length N. N is very large and I don’t know in advance the exact value of N.

How can I most efficiently write a function that will return k completely random numbers from the list

题目非常简单：有N个元素的链表，事先不知道有多长，写一个函数可以高效地从其中取出k个随机数。

初看这题心里没有一点思路，最后查了下资料，这题不是什么新题，编程珠玑Column 12中的题目10提到过，其描述如下：

　　How could you select one of n objects at random, where you see the objects sequentially but you do not know the value of n beforehand? For concreteness, how would you read a text file, and select and print one random line, when you don’t know the number of lines in advance?

　　问题定义可以简化如下：在不知道文件总行数的情况下，如何从文件中随机的抽取一行？

　　首先想到的是我们做过类似的题目吗?当然，在知道文件行数的情况下，我们可以很容易的用C运行库的rand函数随机的获得一个行数，从而随机的取出一行，但是，当前的情况是不知道行数，这样如何求呢？我们需要一个概念来帮助我们做出猜想，来使得对每一行取出的概率相等，也即随机。这个概念即蓄水池抽样（Reservoir Sampling）。

wikipedia：http://en.wikipedia.org/wiki/Reservoir_sampling 说的很详细：

水塘抽样是一系列的随机算法，其目的在于从包含n个项目的集合S中选取k个样本，其中n为一很大或未知的数量，尤其适用于不能把所有n个项目都存放到主内存的情况。最常见例子为Jeffrey Vitter在其论文^[1]中所提及的算法R。

参照Dictionary of Algorithms and Data Structures^[2]所载的O(n)算法，包含以下步骤（假设阵列S以0开始标示）：

從S中抽取首k項放入「水塘」中
對於每一個S[j]項（j ≥ k）：
   隨機產生一個範圍從0到j的整數r
   若 r < k 則把水塘中的第r項換成S[j]項

array R[k];    // result
integer i, j;

// fill the reservoir array
for each i in 1 to k do
    R[i] := S[i]
done;

// replace elements with gradually decreasing probability
for each i in k+1 to length(S) do
    j := random(1, i);   // important: inclusive range
    if j <= k then
        R[j] := S[i]
    fi
done

c++实现：

#include<iostream>
#include<ctime>
using namespace std;

int main()
{
 
    int S[10]={0,1,2,3,4,5,6,7,8,9};
    const int k=4;
    int R[k];
    int i,j;
    for(i=0;i<k;i++)
        R[i]=S[i];

    for(i=k;i<sizeof(S)/sizeof(S[0]);i++)
    {
        srand(time(NULL));
        j=rand()%i;
        if(j<k)
            R[j]=S[i];
    }
    
    for(int i=0;i<k;i++)
        cout<<R[i]<<ends;
    cout<<endl;

}

为什么叫水塘抽样，因为我们array R【k】类似一个reservoir水库（蓄水池），

The algorithm creates a "reservoir" array of size k and populates it with the first k items of S. It then iterates through the remaining elements of S until Sis exhausted. At the i^th element of S, the algorithm generates a random number j between 1 and i. If j is less than k, the j^th element of the reservoir array is replaced with the i^th element of S. In effect, for all i, the i^th element of S is chosen to be included in the reservoir with probability k/i. Similarly, at each iteration the j^th element of the reservoir array is chosen to be replaced with probability j/k * k/i, which simplifies to j/i. It can be shown that when the algorithm has finished executing, each item in S has equal probability (i.e. k/length(S)) of being chosen for the reservoir.

　　有了这个概念，我们来看最先的问题，在不知道文件总行数的情况下，如何从文件中随机的抽取一行？我们便有了这样一个解决方案：定义取出的行号为choice，第一次直接以第一行作为取出行 choice ，而后第二次以二分之一概率决定是否用第二行替换 choice ，第三次以三分之一的概率决定是否以第三行替换 choice ……，以此类推，可用伪代码描述如下：

i = 0

while more input lines

with probability 1.0/++i

choice = this input line

print choice

#include<iostream>
#include<ctime>
using namespace std;

int main()
{
    int choice=0;
    int start=0;
    const int n=10;
    for(int i=2;i<=n;i++)
    {
        srand(time(NULL));
        int randValue=rand()%(i+1-start)+start;
        if(randValue==0)
            choice=i;
    }
    cout<<choice;

}

这种方法的巧妙之处在于成功的构造出了一种方式使得最后可以证明对每一行的取出概率都为1/n（其中n为当前扫描到的文件行数），换句话说对每一行取出的概率均相等，也即完成了随机的选取。

　　证明如下：

回顾这个问题，我们可以对其进行扩展，即如何从未知或者很大样本空间随机地取k个数？

　　类比下即可得到答案，即先把前k个数放入蓄水池，对第k+1，我们以k/(k+1)概率决定是否要把它换入蓄水池，换入时随机的选取一个作为替换项，这样一直做下去，对于任意的样本空间n，对每个数的选取概率都为k/n。也就是说对每个数选取概率相等。

　　伪代码：

Init : a reservoir with the size： k

for i= k+1 to N

    M=random(1, i);

    if( M < k)

     SWAP the Mth value and ith value

end for

　　证明如下：

wikipedia百科的证明好理解一些：

在循环内第n行被抽取的机率为k/n，以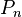 $P_n$ Pn表示。如果档案共有N行，任意第n行(注意这里n是序号，而不是总数）被抽取的机率为:

Pj为第j行选中的概率，为k/j;

为什么要除以k，因为现在求的是单个元素选中的概率，

1-(Pj/k) 就为不选中的概率。

蓄水池抽样问题是一类问题，在这里总结一下，并由衷的感叹这种方法之巧妙，不过对于这种思想产生的源头还是发觉不够，如果能够知道为什么以及怎么样想到这个解决方法的，定会更加有意义。

参考：http://www.cnblogs.com/HappyAngel/archive/2011/02/07/1949762.html

http://zh.wikipedia.org/wiki/%E6%B0%B4%E5%A1%98%E6%8A%BD%E6%A8%A3

可以看以前的：洗牌算法：http://www.cnblogs.com/youxin/p/3348626.html

http://www.cnblogs.com/youxin/p/3353024.html

刷新页面返回顶部

有心故我在

水塘抽样问题

About