代码改变世界

k-medoids

2013-04-16 20:38  youxin  阅读(1000)  评论(0)  编辑  收藏  举报

The k-medoids algorithm is a clustering algorithm related to the k-means algorithm and the medoidshift algorithm. Both the k-means and k-medoids algorithms are partitional (breaking the dataset up into groups) and both attempt to minimize the distance between points labeled to be in a cluster and a point designated as the center of that cluster. In contrast to the k-means algorithm, k-medoids chooses datapoints as centers (medoids or exemplars) and works with an arbitrary matrix of distances between datapoints instead of 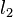l_2. This method was proposed in 1987[1] for the work with l_1 norm and other distances.

k-medoid is a classical partitioning technique of clustering that clusters the data set of n objects into k clusters known a priori. A useful tool for determining k is the silhouette.

It is more robust to noise and outliers as compared to k-means because it minimizes a sum of pairwise dissimilarities instead of a sum of squared Euclidean distances.

A medoid can be defined as the object of a cluster, whose average dissimilarity to all the objects in the cluster is minimal i.e. it is a most centrally located point in the cluster.

The most common realisation of k-medoid clustering is the Partitioning Around Medoids (PAM) algorithm and is as follows:[2]

  1. Initialize: randomly select k of the n data points as the medoids
  2. Associate each data point to the closest medoid. ("closest" here is defined using any valid distance metric, most commonly Euclidean distance, Manhattan distance or Minkowski distance)
  3. For each medoid m
    1. For each non-medoid data point o
      1. Swap m and o and compute the total cost of the configuration
  4. Select the configuration with the lowest cost.
  5. repeat steps 2 to 4 until there is no change in the medoid.

看起来和K-means比较相似，但是K-medoids和K-means是有区别的，不一样的地方在于中心点的选取，在K-means中，我们将中心点取为当前cluster中所有数据点的平均值，在 K-medoids算法中，我们将从当前cluster 中选取这样一个点——它到其他所有（当前cluster中的）点的距离之和最小——作为中心点。

K-MEANS算法的缺点：
产生类的大小相差不会很大，对于脏数据很敏感。
改进的算法：K-medoids方法。

这儿选取一个对象叫做mediod来代替上面的中心的作用，这样的一个medoid就标识了这个类。

K-MEDODIS的具体流程如下：
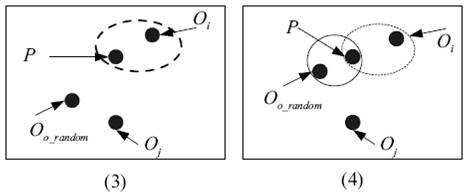
1）任意选取K个对象作为medoids（O1,O2,…Oi…Ok）。　　
2）将余下的对象分到各个类中去（根据与medoid最相近的原则）；　　
3）对于每个类（Oi）中，顺序选取一个Or，计算用Or代替Oi后的消耗—E（Or）。选择E最小的那个Or来代替Oi。这样K个medoids就改变了。
4）重复2、3步直到K个medoids固定下来。　　
不容易受到那些由于误差之类的原因产生的脏数据的影响，但计算量显然要比K-means要大，一般只适合小数据量。

http://en.wikipedia.org/wiki/K-medoids