虚树

虚树用于将一棵树的无意义点删除， 只保留关键点和树的结构， 优化树形dp的速度。

构建虚树

初始化一个栈， 将根节点入栈(必须保留根节点以供遍历)， 然后根据\(dfn\)序遍历这颗树。

遍历途中把关键点依次入栈, 当要添加一个新的关键点(\(v\))时， 求\(v\)与栈顶(\(stk[top]\))的\(lca(v, stk[top])\)，此时有几种情况：

1. \(lca(v, stk[top]) = stk[top]\) ，直接入栈。

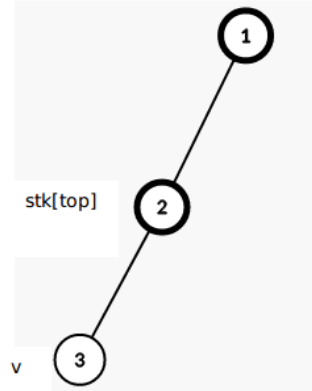
2. \(lca(v, stk[top])\ != stk[top]\)

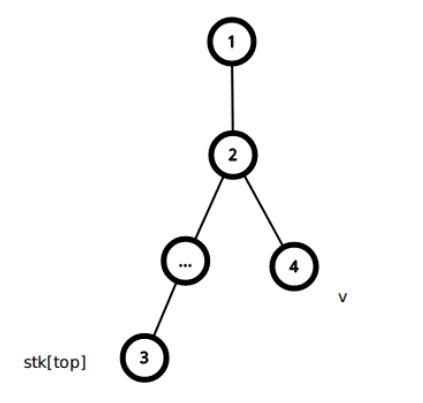
此时\(stk[top]\)所在子树必定已经处理完毕， 所以可以开始构建虚树。

将\(stk[top]\)和\(stk[top - 1]\)连边， 然后将\(stk[top]\)出栈， 接下来原来的\(stk[top - 1]\)变成\(stk[top]\), 然后如此循环， 直到\(stk[top-1]\)深度小于等于\(lca(v, stk[top])\)。

如果\(lca(v, stk[top])\)在栈内即\(stk[top-1]\)深度等于\(lca(v, stk[top])\)，将\(stk[top]\)与\(lca(v, stk[top])\)连边， \(stk[top]\)出栈即可。

如果\(lca(v, stk[top])\)不在栈内即\(stk[top-1]\)深度小于\(lca(v, stk[top])\)，

图中 lca 指 lca(v, stk[top])

因为此时需要保留树的结构， 所以将\(stk[top]\)与\(lca(v, stk[top])\)连边， \(stk[top]\)出栈，\(lca(v, stk[top])\)入栈， 向\(v\)方向继续遍历。

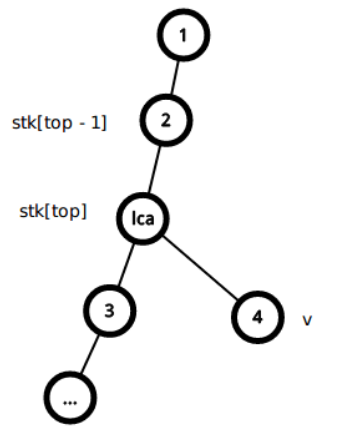
处理完成后的情况

此时左子树已经完全出栈， 栈内只存在一条链。

遍历完之后， 栈内也只存在一条链， 依次退栈， 也要把\(stk[top]\)与\(stk[top-1]\)连边。

例题(P2495 消耗战)

gyz大佬的题解和代码

考虑普通的\(DP\)，令\(f_u\)表示切断\(u\)的子树中的所有点的代价，\(g_u\)表示从\(u\)到根节点的路径上最小的边权,分两种情况，如果\(u\)上边有资源，那么不管子树怎么样，\(u\)都要与根节点分离，即\(f_u=g_u\)，否则就是\(min(g_u,\sum_{v|son}f_v)\)，但是这样做显然会T的飞起，考虑怎么优化一下。看到虽然询问次数很多但是询问的点不是很多，每次暴力DP的时候都把时间浪费在了搜索无关的点上边，如果把这些时间略掉就应该可以通过此题。 于是需要用到虚树，每次建一棵虚树，在虚树上边\(DP\)，就可以完美\(AC\)，注意一点就是虚树上边所有的点都需要与根节点断开联系，所以不存在\(f\)值为0的情况。

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=25e4+10;
struct Edge{
	int to,nxt,val;
}e[N<<2];
int h[N],idx;
void Ins(int a,int b,int c){
	e[++idx].to=b;e[idx].nxt=h[a];
	e[idx].val=c;h[a]=idx;
}
long long wv[N];
int dep[N],siz[N],son[N],fa[N];
void dfs1(int u){
	siz[u]=1;
	for(int i=h[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v==fa[u])continue;
		fa[v]=u;
		dep[v]=dep[u]+1;
		wv[v]=min(wv[u],1ll*e[i].val);
		dfs1(v);
		siz[u]+=siz[v];
		if(siz[son[u]]<siz[v])son[u]=v;
	}
}
int dfn[N],Time,trtop[N];
void dfs2(int u,int tt){
	dfn[u]=++Time;
	trtop[u]=tt;
	if(son[u])dfs2(son[u],tt);
	for(int i=h[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v==fa[u]||v==son[u])continue;
		dfs2(v,v);
	}
}
int lca(int x,int y){
	while(trtop[x]!=trtop[y]){
		if(dep[trtop[x]]<dep[trtop[y]])y=fa[trtop[y]];
		else x=fa[trtop[x]];
	}
	return dep[x]>dep[y]?y:x;
}
int a[N],top,stk[N];
bool cmp(int a,int b){
	return dfn[a]<dfn[b];
}
void Insert(int w){
	if(!top){
		stk[++top]=w;
		return;
	}
	int ance=lca(w,stk[top]);
	if(top>1&&stk[top]==ance)return;
	while(top>1&&dep[stk[top-1]]>=dep[ance]){
		Ins(stk[top-1],stk[top],0);
		top--;
	}
	if(stk[top]!=ance)Ins(ance,stk[top],0),stk[top]=ance;
	stk[++top]=w;
}
long long dfs3(int u){
	if(h[u]==0)return wv[u];
	long long t=0;
	for(int i=h[u];i;i=e[i].nxt){
		int v=e[i].to;
		t+=dfs3(v);
	}
	h[u]=0;
	return min(t,1ll*wv[u]);
}
int main(){
	int n;
	scanf("%d",&n);
	for(int i=1;i<n;i++){
		int a,b,c;
		scanf("%d%d%d",&a,&b,&c);
		Ins(a,b,c);Ins(b,a,c);
	}
	wv[1]=0x7f7f7f7f7f7f7f7f;
	dfs1(1);
	dfs2(1,1);
	memset(h,0,sizeof(h));
	int T;
	scanf("%d",&T);
	while(T--){
		int m;idx=0;
		scanf("%d",&m);
		for(int i=1;i<=m;i++)
			scanf("%d",&a[i]);
		sort(a+1,a+m+1,cmp);
		if(a[1]!=1)stk[++top]=1;
		for(int i=1;i<=m;i++){
			Insert(a[i]);
		}
		if(top)while(--top)Ins(stk[top],stk[top+1],0);
		printf("%lld\n",dfs3(1));
	}
}