Emergency Evacuation 题解

The Japanese government plans to increase the number of inbound tourists to forty million in the year 2020, and sixty million in 2030. Not only increasing touristic appeal but also developing
tourism infrastructure further is indispensable to accomplish such numbers.

One possible enhancement on transport is providing cars extremely long and/or wide, carrying many passengers at a time. Too large a car, however, may require too long to evacuate all
passengers in an emergency. You are requested to help estimating the time required.

The car is assumed to have the following seat arrangement.

• A center aisle goes straight through the car, directly connecting to the emergency exit
  door at the rear center of the car.
• The rows of the same number of passenger seats are on both sides of the aisle.
  A rough estimation requested is based on a simple step-wise model. All passengers are initially
  on a distinct seat, and they can make one of the following moves in each step.
• Passengers on a seat can move to an adjacent seat toward the aisle. Passengers on a seat
  adjacent to the aisle can move sideways directly to the aisle.
• Passengers on the aisle can move backward by one row of seats. If the passenger is in front of the emergency exit, that is, by the rear-most seat rows, he/she can get off the car.

The seat or the aisle position to move to must be empty; either no other passenger is there before the step, or the passenger there empties the seat by moving to another position in the
same step. When two or more passengers satisfy the condition for the same position, only one of them can move, keeping the others wait in their original positions.

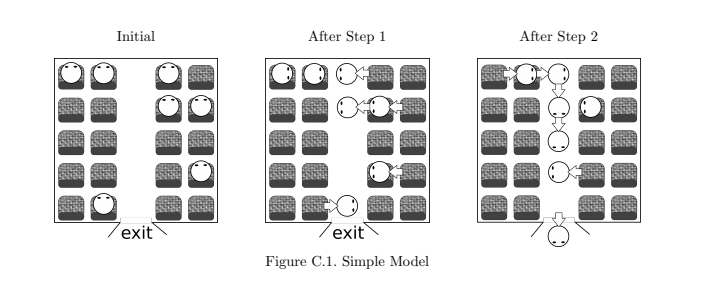
The leftmost figure of Figure C.1 depicts the seat arrangement of a small car given in Sample Input 1. The car have five rows of seats, two seats each on both sides of the aisle, totaling twenty. The initial positions of seven passengers on board are also shown.

The two other figures of Figure C.1 show possible positions of passengers after the first and the second steps. Passenger movements are indicated by fat arrows. Note that, two of the passengers in the front seat had to wait for a vacancy in the first step, and one in the second row had to wait in the next step.

Your task is to write a program that gives the smallest possible number of steps for all the passengers to get off the car, given the seat arrangement and passengers’ initial positions.

输入格式

The input consists of a single test case of the following format.

put consists of a single test case of the following format.

\( r\ s\ p\\ i_1\ j_1\\ .\\ .\\ .\\ i_p\ j_p\\ \)

Here, \(r\) is the number of passenger seat rows, \(s\) is the number of seats on each side of the aisle, and \(p\) is the number of passengers. They are integers satisfying \(1 \le r \le 500, 1 \le s \le 500\), and \(1 \le p \le 2rs\).

The following \(p\) lines give initial seat positions of the passengers. The k-th line with ik and \(jk\) means that the k-th passenger’s seat is in the ik-th seat row and it is the jk-th seat on that row.

Here, rows and seats are counted from front to rear and left to right, both starting from one.

They satisfy \(1 \le ik \le r\) and \(1 \le jk \le 2s\). Passengers are on distinct seats, that \(i_s, i_k \ne i_l\) or \(j_k \ne j_l\) holds if \(k \ne l\).

输出格式

The output should be one line containing a single integer, the minimum number of steps required for all the passengers to get off the car.

样例输入1

5 2 7
1 1
1 2
1 3
2 3
2 4
4 4
5 2

样例输出1

9

样例输入2

500 500 16
1 1
1 2
1 999
1 1000
2 1
2 2
2 999
2 1000
3 1
3 2
3 999
3 1000
499 500
499 501
499 999
499 1000

样例输出2

1008

题解

这个题还有点绕,但是想通了之后就简单了

首先假设不会有人挡住别人,这样很容易求出来每个人的时间,但是这时候就会发现,会有人一起到达出口,而假设实际上是不成立的,所以需要依次延后.

比如某个时间有3个人同时到达了出口,那么这一秒只能有一个人出去,而剩下的两个人只能再接下来的两秒出去.

这又遇到一个问题,如果这两个人等待的时候,后面又有人被堵了,怎么办?只能继续延后,这样延后到都出去.

如果真的是一个一个出去的话,显然答案就是人数,但是实际上可能又空缺,而这个空缺数量也不难算,当出口出现堵塞的时候,看看最后延后到哪里,如果从现在到堵塞结束的时间都没有人到达出口,就出现了空缺.

把接下来第一个到达出口的时间和堵塞结束的时间相减,就得出了空缺大小,人数加上总的空缺大小,就是最后的答案

代码

#include <cstdio>
#define max(a, b) ((a) > (b) ? (a) : (b))
int cnt[2010], r, s, p, y, x, last, ans;
int main() {
    scanf("%d%d%d", &r, &s, &p);
    for (int i = 1; i <= p; i++) {
        scanf("%d%d", &y, &x);
        cnt[max(s - x + 1, x - s) + r - y + 1]++;  // 下标是时间,记录这个时间有多少人到达出口(若人不挡人)
    }
    for (int i = 1; i < 2010; i++)
        if (cnt[i])
            if (last >= i - 1) // last是堵塞结束的时间
                last = cnt[i] + last;  // 继续延后
            else {
                ans += i - last - 1;  // 记录空缺
                last = i - 1 + cnt[i];  // 更新last
            }
    printf("%d", ans + p);
    return 0;
}