P1117 [NOI2016] 优秀的拆分 SA+DP

题意：

戳这里

分析：

对于要求的东西我们可以 DP 求一下，我们设 \(f[i]\) 表示以 \(i\) 结尾的 \(AA\) 类型的串的个数，\(g[i]\) 表示以 \(i\) 开头的 \(AA\) 类型的串的个数 \(ans=\sum f[i]\times g[i+1]\)

所以我们现在考虑如何求 \(f,g\) ,首先我们有一个 \(n^2\) 暴力的想法，直接枚举两个相邻串判相同

然后我们考虑优化，我们考虑枚举长度\(len\), 每\(len\)个点标记一下，显然每一个长度为 \(2\times len\) 的串必定会经过两个标记点，那么我们考虑相邻的两个标记点会带来什么贡献，显然对于标记点 \(i,j\) ,记他们的后缀的 \(lcp\) 和前缀的 \(lcs\)

1. 如果 \(lcp+lcs<len\) 那么这两个点不会产生 \(AA\) 类型的串

2. 如果 \(lcp+lcs>=len\) 那么如下图所示（图源其他巨佬的博客，侵删）

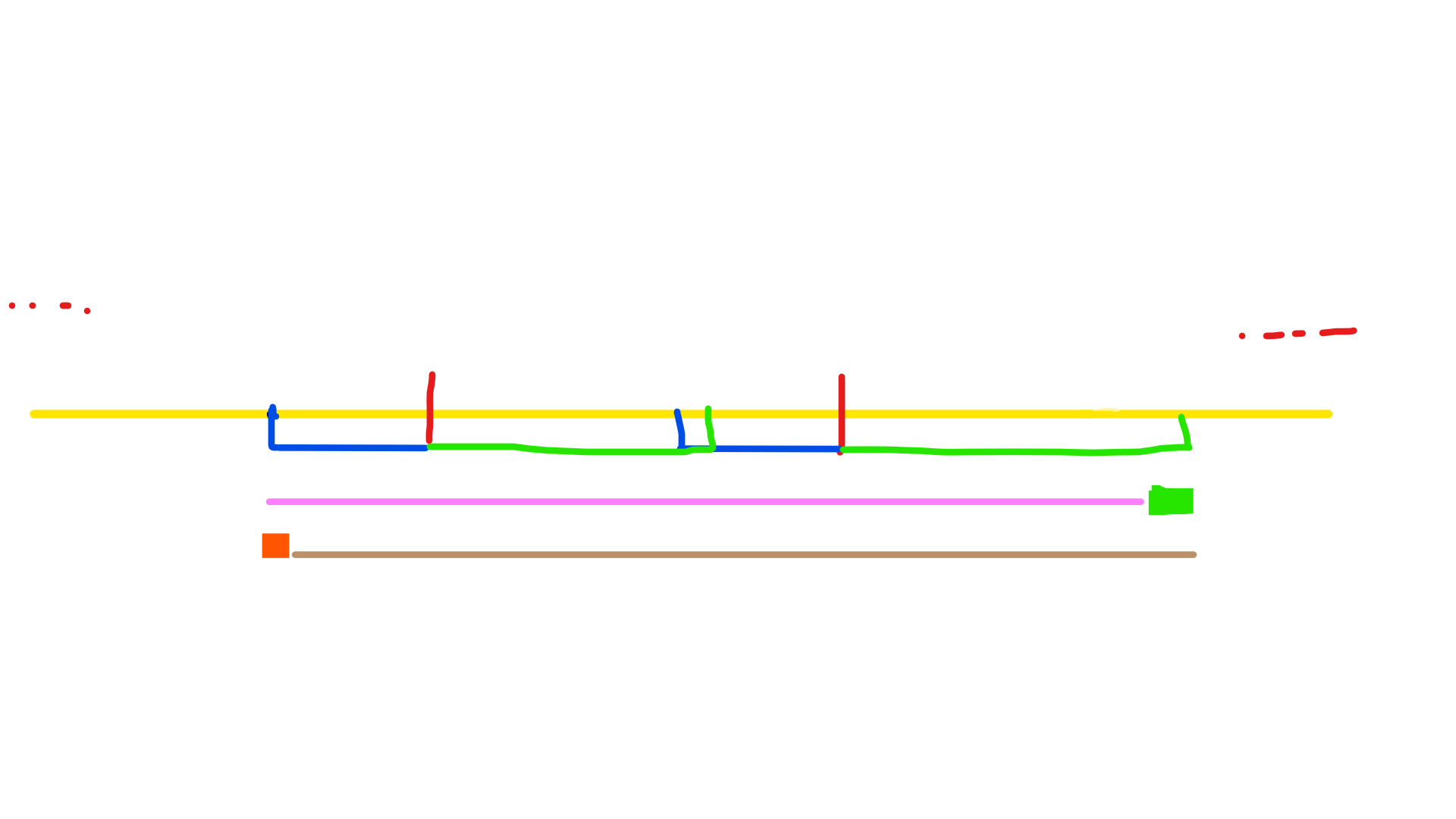
粉色串表示第一个合法的 \(f\) 串，从它开始向后可以一直扩展到绿色荧光笔结尾，这些点都可以作为 \(AA\) 类型的结尾，那么我们给段区间的每一个点 \(f\) 都加 1

褐色串表示后缀，区间同理

求 \(lcp,lcs\) 可以通过 \(SA\) 和 \(ST\) 表\(O(n\log)\)预处理，\(O(1)\) 查询,然后我们对区间加的操作差分处理，就可以在 \(O(n\log)\) 的复杂度内求出 \(f,g\)

代码：

#include<bits/stdc++.h>

using namespace std;

namespace zzc
{
	const int maxn = 3e4+5;
	int t,n;
	long long ans;
	char ch[maxn];
	int lg[maxn],f[maxn],g[maxn];
	
	struct suffix_array
	{
		int sa[maxn],rk[maxn],ht[maxn][20],cnt[maxn],oldrk[maxn],tmp[maxn],id[maxn];
		
		bool check(int x,int y,int k)
		{
			return oldrk[x]==oldrk[y]&&oldrk[x+k]==oldrk[y+k];
		}
		
		void build()
		{
			int num=26;
			for(int i=1;i<=n;i++) cnt[rk[i]=ch[i]-'a'+1]++;
			for(int i=1;i<=num;i++) cnt[i]+=cnt[i-1];
	        for(int i=n;i;i--) sa[cnt[rk[i]]--]=i;
	        for(int t=1;t<=n;t<<=1)
	        {
	            int tot=0;
	            for(int i=n-t+1;i<=n;i++) id[++tot]=i;
	            for(int i=1;i<=n;i++) if(sa[i]>t) id[++tot]=sa[i]-t;
	            tot=0;
	            memset(cnt,0,sizeof(cnt));
	            for(int i=1;i<=n;i++) cnt[tmp[i]=rk[id[i]]]++;
	            for(int i=1;i<=num;i++) cnt[i]+=cnt[i-1];
	            for(int i=n;i;i--) sa[cnt[tmp[i]]--]=id[i];
	            memcpy(oldrk,rk,sizeof(rk));
	            for(int i=1;i<=n;i++) rk[sa[i]]=check(sa[i-1],sa[i],t)?tot:++tot;
	            num=tot;
	        }
	        for(int i=1,j=0;i<=n;i++)
	        {
	            if(j)j--;
	            while(ch[i+j]==ch[sa[rk[i]-1]+j]) j++;
	            ht[rk[i]][0]=j;
	        }
	        for(int j=1;j<=18;j++)
	        {
	            for(int i=1;i+(1<<j)-1<=n;i++)
	            {
	                ht[i][j]=min(ht[i][j-1],ht[i+(1<<(j-1))][j-1]);
	            }
	        }
		}
		
		int query(int ql,int qr)
		{
			int l=min(rk[ql],rk[qr])+1,r=max(rk[ql],rk[qr]);
			int t=lg[r-l+1];
			return min(ht[l][t],ht[r-(1<<t)+1][t]);
		}
		
		void clear()
		{
			memset(sa,0,sizeof(sa));
			memset(rk,0,sizeof(rk));
			memset(cnt,0,sizeof(cnt));
			memset(ht,0,sizeof(ht));
			memset(tmp,0,sizeof(tmp));
		}
		
	}s1,s2;
	
	void clear()
	{
		s1.clear();s2.clear();
		memset(f,0,sizeof(f));
		memset(g,0,sizeof(g));
		ans=0;
	}
	
	void work()
	{
		lg[0]=-1;for(int i=1;i<=30000;i++) lg[i]=lg[i>>1]+1;
		scanf("%d",&t);
		while(t--)
		{
			scanf("%s",ch+1);n=strlen(ch+1);
			s1.build();
			reverse(&ch[1],&ch[n+1]);
			s2.build();
			for(int len=1;len<=n/2;len++)
			{
				for(int i=len,j=i+len;j<=n;i+=len,j+=len)
				{
					int lcp=min(s1.query(i,j),len),lcs=min(s2.query(n-i+2,n-j+2),len-1);
					int tmp=lcp+lcs-len+1;
					if(lcp+lcs>=len)
					{
						g[i-lcs]++;g[i-lcs+tmp]--;
						f[j+lcp-tmp]++;f[j+lcp]--;
					}
				}
			}
			for(int i=1;i<=n;i++) f[i]+=f[i-1],g[i]+=g[i-1];
			for(int i=1;i<n;i++) ans+=1ll*f[i]*g[i+1];
			printf("%lld\n",ans);
			clear();
		}
	}
	
}

int main()
{
	zzc::work();
	return 0;
}