Splay伸展树学习笔记
Splay伸展树
有篇Splay入门必看文章 —— CSDN链接
经典引文
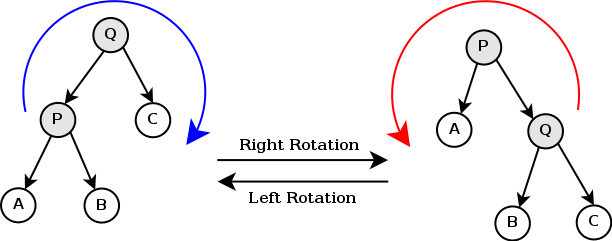
- 节点x是父节点p的左孩子还是右孩子
- 节点p是不是根节点,如果不是
- 节点p是父节点g的左孩子还是右孩子

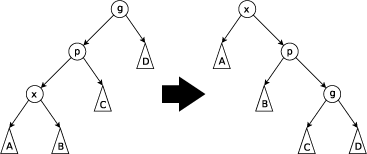
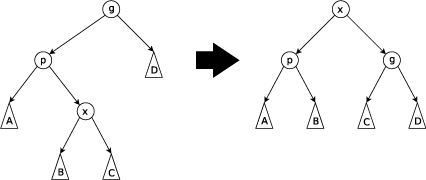
自学笔记
今天开始自己动手写Splay。身边的小伙伴大多是用下标和数组来维系各个结点的联系,但是我还是一如既往的喜欢C++的指针(❤ ω ❤)。
结点以一个struct结构体的形式存在。
struct node { int value; node *father; node *son[2]; node (int v = 0, node *f = NULL) { value = v; father = f; son[0] = NULL; son[1] = NULL; } };
其中,son[0]代表左儿子,son[1]代表右儿子。
用一个函数来判断子节点是父节点的哪个儿子。
inline bool son(node *f, node *s) { return f->son[1] == s; }
返回值就是son[]数组的下标,这个函数很方便。
最关键的是旋转操作,有别于常见的zig,zag旋转,我喜欢用一个函数实现其两者的功能,即rotate(x)代表将x旋转到其父节点的位置上。
inline void rotate(node *t) { node *f = t->father; node *g = f->father; bool a = son(f, t), b = !a; f->son[a] = t->son[b]; if (t->son[b] != NULL) t->son[b]->father = f; t->son[b] = f; f->father = t; t->father = g; if (g != NULL) g->son[son(g, f)] = t; else root = t; }
函数会自行判断x实在父节点的左儿子上还是右儿子上,并自动左旋或右旋。这里要注意改变祖父结点的儿子指针,以及结点的父亲指针,切忌马虎漏掉。同时还要事先做好特判,放止访问非法地址。这里用指针相较于用下标的一个好处就是,如果你不小心访问了NULL即空指针,也是下标党常用的0下标,指针写法一定会RE,而下标写法可能就不会崩溃,因而不易发现错误,导致一些较为复杂而智障的错误。
然后是核心函数——Splay函数,貌似也有人叫Spaly的样子,然而我并没有考证什么。Splay(x,y)用于将x结点旋转到y结点的某个儿子上。特别地,Splay(x,NIL)代表将x旋转到根节点的位置上。根节点的父亲一般是NIL或0。
inline void spaly(node *t, node *p) { while (t->father != p) { node *f = t->father; node *g = f->father; if (g == p) rotate(t); else { if (son(g, f) ^ son(f, t)) rotate(t), rotate(t); else rotate(f), rotate(t); } } }
这里值得注意的是两种双旋。如果t(该节点),f(父亲节点),g(祖父节点)形成了一条单向的链,即[右→右]或[左→左]这样子,那么就先对父亲结点进行rotate操作,再对该节点进行rotate操作;否则就对该节点连续进行两次rotate操作。据称单旋无神犇,双旋O(logN),这句话我也没有考证,个人表示不想做什么太多的探究,毕竟Splay的复杂度本来就挺玄学的了,而且专门卡单旋Splay的题也没怎么听说过。对了,这个双旋操作和AVL的双旋是不是有那么几分相似啊,虽然还是不太一样的吧,好吧其实也不怎么像╮(╯-╰)╭。
接下来谈谈插入操作。插入操作就和普通的二叉搜索树类似,先找到合适的叶子结点,然后在空着的son[]上新建结点,把值放入。不同的是需要把新建的结点Splay到根节点位置,复杂度需要,不要问为什么。
inline void insert(int val) { if (root == NULL) root = new node(val, NULL); for (node *t = root; t; t = t->son[val >= t->value]) { if (t->value == val) { spaly(t, NULL); return; } if (t->son[val >= t->value] == NULL) t->son[val >= t->value] = new node(val, t); } }
注意,这个插入函数实现的是非重集合。
与之对应的就是删除操作,相对的复杂一些。删除一个元素,需要先在树中找到这个结点,然后把这个结点Splay到根节点位置,开始分类讨论。如果这个结点没有左儿子(左子树),直接把右儿子放在根的位置上即可;否则的话就需要想方设法合并左右子树:在左子树种找到最靠右(最大)的结点,把它旋转到根节点的儿子上,此时它一定没有右儿子,因为根节点的左子树中不存在任何一个元素比它更大,那么把根节点的右子树接在这个结点的右儿子上即可。
inline void erase(int val) { node *t = root; for ( ; t; ) { if (t->value == val) break; t = t->son[val > t->value]; } if (t != NULL) { spaly(t, NULL); if (t->son[0] == NULL) { root = t->son[1]; if (root != NULL) root->father = NULL; } else { node *p = t->son[0]; while (p->son[1] != NULL) p = p->son[1]; spaly(p, t); root = p; root->father = NULL; p->son[1] = t->son[1]; if (p->son[1] != NULL) p->son[1]->father = p; } } }
相较于insert()确实复杂了不少。
以上就是Splay的框架了,是Splay必不可少的部分,在此基础上可以加入许多新的功能。
例如,手动实现垃圾回收,这样新建结点的常数会小很多,毕竟C++的new是很慢的。
node tree[siz], *stk[siz]; int top; inline node *newnode(int v, node *f) { node *ret = stk[--top]; ret->size = 1; ret->value = v; ret->father = f; ret->son[0] = NULL; ret->son[1] = NULL; ret->reverse = false; return ret; } inline void freenode(node *t) { stk[top++] = t; }
有的时候需要我们维护子树大小。
inline int size(node *t) { return t == NULL ? 0 : t->size; } inline void update(node *t) { t->size = 1; t->size += size(t->son[0]); t->size += size(t->son[1]); }
简单,安全。
维护区间翻转的时候需要用到打标记的方式。
inline bool tag(node *t) { return t == NULL ? false : t->reverse; } inline void reverse(node *t) { if (t != NULL) t->reverse ^= true; } inline void pushdown(node *t) { if (tag(t)) { std::swap(t->son[0], t->son[1]); reverse(t->son[0]); reverse(t->son[1]); t->reverse ^= true; } }
还有更为简洁的rotate函数。
inline void connect(node *f, node *s, bool k) { if (f == NULL) root = s; else f->son[k] = s; if (s != NULL) s->father = f; } inline void rotate(node *t) { node *f = t->father; node *g = f->father; bool a = son(f, t), b = !a; connect(f, t->son[b], a); connect(g, t, son(g, f)); connect(t, f, b); update(f); update(t); }
@Author: YouSiki


 浙公网安备 33010602011771号
浙公网安备 33010602011771号