Codeforces Round #379 (Div. 2)

A. Anton and Danik

Anton likes to play chess, and so does his friend Danik.

Once they have played n games in a row. For each game it's known who was the winner — Anton or Danik. None of the games ended with a tie.

Now Anton wonders, who won more games, he or Danik? Help him determine this.

Input

The first line of the input contains a single integer n (1 ≤ n ≤ 100 000) — the number of games played.

The second line contains a string s, consisting of n uppercase English letters 'A' and 'D' — the outcome of each of the games. The i-th character of the string is equal to 'A' if the Anton won the i-th game and 'D' if Danik won the i-th game.

Output

If Anton won more games than Danik, print "Anton" (without quotes) in the only line of the output.

If Danik won more games than Anton, print "Danik" (without quotes) in the only line of the output.

If Anton and Danik won the same number of games, print "Friendship" (without quotes).

 

问字符串中是A多还是D多，亦或者是一样多的水题。

#include <bits/stdc++.h>
using namespace std;

signed main(void)
{
    int n; cin >> n;
    string s; cin >> s;
    
    int t = 0;
    
    for (auto i : s)
        if (i == 'A')
            ++t;
        else
            --t;
    
    if (!t)
        cout << "Friendship" << endl;
    else if (t > 0)
        cout << "Anton" << endl;
    else
        cout << "Danik" << endl;
}

 

B. Anton and Digits

Recently Anton found a box with digits in his room. There are k2 digits 2, k3 digits 3, k5 digits 5 and k6 digits 6.

Anton's favorite integers are 32 and 256. He decided to compose this integers from digits he has. He wants to make the sum of these integers as large as possible. Help him solve this task!

Each digit can be used no more than once, i.e. the composed integers should contain no more than k2 digits 2, k3 digits 3 and so on. Of course, unused digits are not counted in the sum.

Input

The only line of the input contains four integers k2, k3, k5 and k6 — the number of digits 2, 3, 5 and 6 respectively (0 ≤ k2, k3, k5, k6 ≤ 5·106).

Output

Print one integer — maximum possible sum of Anton's favorite integers that can be composed using digits from the box.

 

问用k2个2，k3个3，k5个5，k6个6，能组合出的32和256中最大的和。

贪心地优先组合256，然后尽可能多地组合32即可。

#include <bits/stdc++.h>
using namespace std;

signed main(void)
{
    int a, b, c, d, t, ans;
    cin >> a >> b >> c >> d;
    
    t = min(a, min(c, d));
    ans = t * 256;
    a -= t;
    t = min(a, b);
    ans += t * 32;
    cout << ans << endl;
}

 

C. Anton and Making Potions

Anton is playing a very interesting computer game, but now he is stuck at one of the levels. To pass to the next level he has to prepare npotions.

Anton has a special kettle, that can prepare one potions in x seconds. Also, he knows spells of two types that can faster the process of preparing potions.

1. Spells of this type speed up the preparation time of one potion. There are m spells of this type, the i-th of them costs bi manapoints and changes the preparation time of each potion to ai instead of x.
2. Spells of this type immediately prepare some number of potions. There are k such spells, the i-th of them costs di manapoints and instantly create ci potions.

Anton can use no more than one spell of the first type and no more than one spell of the second type, and the total number of manapoints spent should not exceed s. Consider that all spells are used instantly and right before Anton starts to prepare potions.

Anton wants to get to the next level as fast as possible, so he is interested in the minimum number of time he needs to spent in order to prepare at least n potions.

Input

The first line of the input contains three integers n, m, k (1 ≤ n ≤ 2·109, 1 ≤ m, k ≤ 2·105) — the number of potions, Anton has to make, the number of spells of the first type and the number of spells of the second type.

The second line of the input contains two integers x and s (2 ≤ x ≤ 2·109, 1 ≤ s ≤ 2·109) — the initial number of seconds required to prepare one potion and the number of manapoints Anton can use.

The third line contains m integers ai (1 ≤ ai < x) — the number of seconds it will take to prepare one potion if the i-th spell of the first type is used.

The fourth line contains m integers bi (1 ≤ bi ≤ 2·109) — the number of manapoints to use the i-th spell of the first type.

There are k integers ci (1 ≤ ci ≤ n) in the fifth line — the number of potions that will be immediately created if the i-th spell of the second type is used. It's guaranteed that ci are not decreasing, i.e. ci ≤ cj if i < j.

The sixth line contains k integers di (1 ≤ di ≤ 2·109) — the number of manapoints required to use the i-th spell of the second type. It's guaranteed that di are not decreasing, i.e. di ≤ dj if i < j.

Output

Print one integer — the minimum time one has to spent in order to prepare n potions.

 

需要制造n瓶毒药（也许是饮料，不知道），制造一瓶需要x单位时间。现在有2类魔法，每类最多只能使用一种且一次。

魔法一：有m种，花费bi金钱，使得制造一瓶毒药的时间变成ai。

魔法二：有k种，花费di金钱，使得在0单位时间内制造ci瓶毒药。

先给出最多花费金钱，求最小完成时间。

 

对于每种魔法，按照花费从小到大排序后，花费大而效果差的一定没用，直接忽略即可。

筛出两个按照花费单调上升的魔法序列，从左向右枚举一种魔法的时候，根据最大金钱的限制，另一种魔法对应的最优决策一定是从右向左，维护两个指针即可。

#include <bits/stdc++.h>
using namespace std;

#define N 200005
#define int long long

typedef long long LL;
typedef pair<int, int> pr;

int n, m, k, c, s;

pr sp1[N]; int t1;
pr sp2[N]; int t2;

signed main(void)
{
    cin >> n >> m >> k >> c >> s;
    
    for (int i = 1; i <= m; ++i)
        cin >> sp1[i].second;
        
    for (int i = 1; i <= m; ++i)
        cin >> sp1[i].first;
        
    for (int i = 1; i <= k; ++i)
        cin >> sp2[i].second;
    
    for (int i = 1; i <= k; ++i)
        cin >> sp2[i].first;
        
    sp1[++m] = make_pair(0, c);
    sp2[++k] = make_pair(0, 0);
        
    sort(sp1 + 1, sp1 + 1 + m);
    sort(sp2 + 1, sp2 + 1 + k);
    
    t1 = t2 = 0;
    
    for (int i = 1; i <= m; ++i)if (sp1[i].first <= s)
        if (!t1 || sp1[i].second < sp1[t1].second)sp1[++t1] = sp1[i];
            
    for (int i = 1; i <= k; ++i)if (sp2[i].first <= s)
        if (!t2 || sp2[i].second > sp2[t2].second)sp2[++t2] = sp2[i];
        
    if (sp1[t1].second <= 0)return puts("0"), 0;
    if (sp2[t2].second >= n)return puts("0"), 0;
    
    LL answer = 4e18 + 7;
    
    for (int i = 1, j = t1; i <= t2; ++i)
    {
        while (j && sp1[j].first + sp2[i].first > s)--j;
            
        if (j)answer = min(answer, (LL)sp1[j].second * (n - sp2[i].second));
    }
    
    cout << answer << endl;
}

 

D. Anton and Chess

Anton likes to play chess. Also, he likes to do programming. That is why he decided to write the program that plays chess. However, he finds the game on 8 to 8 board to too simple, he uses an infinite one instead.

The first task he faced is to check whether the king is in check. Anton doesn't know how to implement this so he asks you to help.

Consider that an infinite chess board contains one white king and the number of black pieces. There are only rooks, bishops and queens, as the other pieces are not supported yet. The white king is said to be in check if at least one black piece can reach the cell with the king in one move.

Help Anton and write the program that for the given position determines whether the white king is in check.

Remainder, on how do chess pieces move:

• Bishop moves any number of cells diagonally, but it can't "leap" over the occupied cells.
• Rook moves any number of cells horizontally or vertically, but it also can't "leap" over the occupied cells.
• Queen is able to move any number of cells horizontally, vertically or diagonally, but it also can't "leap".

Input

The first line of the input contains a single integer n (1 ≤ n ≤ 500 000) — the number of black pieces.

The second line contains two integers x0 and y0 ( - 109 ≤ x0, y0 ≤ 109) — coordinates of the white king.

Then follow n lines, each of them contains a character and two integers xi and yi ( - 109 ≤ xi, yi ≤ 109) — type of the i-th piece and its position. Character 'B' stands for the bishop, 'R' for the rook and 'Q' for the queen. It's guaranteed that no two pieces occupy the same position.

Output

The only line of the output should contains "YES" (without quotes) if the white king is in check and "NO" (without quotes) otherwise.

 

在无限大的国际象棋棋盘上，给出白子King的位置，以及一些黑子的种类(后，车，象）和位置，求是否in check。注意棋子不能 越“子”强杀。

 

枚举王的8个方向，看最近的棋子是否符合这个方向即可。

#include <bits/stdc++.h>
using namespace std;

#define N 500005
#define inf 2e9 + 7

int n;
int tx;
int ty;
int vis[8];
int dis[8];

signed main(void)
{
    cin >> n >> tx >> ty;
    
    for (int i = 0; i < 8; ++i)
        dis[i] = inf;
    
    for (int i = 1; i <= n; ++i)
    {
        char c; int x, y; 
        cin >> c >> x >> y;

        if (x == tx && y < ty && ty - y < dis[0])
            dis[0] = ty - y, vis[0] = (c == 'Q' || c == 'R');
        if (x == tx && y > ty && y - ty < dis[1])
            dis[1] = y - ty, vis[1] = (c == 'Q' || c == 'R');
        if (y == ty && x < tx && tx - x < dis[2])
            dis[2] = tx - x, vis[2] = (c == 'Q' || c == 'R');
        if (y == ty && x > tx && x - tx < dis[3])
            dis[3] = x - tx, vis[3] = (c == 'Q' || c == 'R');
            
        if (tx + ty == x + y && x < tx && tx - x < dis[4])
            dis[4] = tx - x, vis[4] = (c == 'Q' || c == 'B');
        if (tx + ty == x + y && x > tx && x - tx < dis[5])
            dis[5] = x - tx, vis[5] = (c == 'Q' || c == 'B');
        if (tx - ty == x - y && x < tx && tx - x < dis[6])
            dis[6] = tx - x, vis[6] = (c == 'Q' || c == 'B');
        if (tx - ty == x - y && x > tx && x - tx < dis[7])
            dis[7] = x - tx, vis[7] = (c == 'Q' || c == 'B');
    }
    
    int answer = 0;
    
    for (int i = 0; i < 8; ++i)
        answer |= vis[i];
        
    puts(answer ? "YES" : "NO");
}

 

E. Anton and Tree

Anton is growing a tree in his garden. In case you forgot, the tree is a connected acyclic undirected graph.

There are n vertices in the tree, each of them is painted black or white. Anton doesn't like multicolored trees, so he wants to change the tree such that all vertices have the same color (black or white).

To change the colors Anton can use only operations of one type. We denote it as paint(v), where v is some vertex of the tree. This operation changes the color of all vertices u such that all vertices on the shortest path from v to u have the same color (including v and u). For example, consider the tree

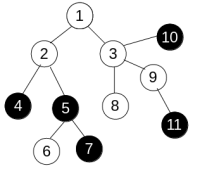
and apply operation paint(3) to get the following:

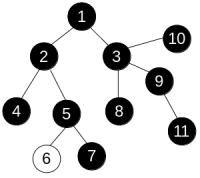
Anton is interested in the minimum number of operation he needs to perform in order to make the colors of all vertices equal.

Input

The first line of the input contains a single integer n (1 ≤ n ≤ 200 000) — the number of vertices in the tree.

The second line contains n integers colori (0 ≤ colori ≤ 1) — colors of the vertices. colori = 0 means that the i-th vertex is initially painted white, while colori = 1 means it's initially painted black.

Then follow n - 1 line, each of them contains a pair of integers ui and vi (1 ≤ ui, vi ≤ n, ui ≠ vi) — indices of vertices connected by the corresponding edge. It's guaranteed that all pairs (ui, vi) are distinct, i.e. there are no multiple edges.

Output

Print one integer — the minimum number of operations Anton has to apply in order to make all vertices of the tree black or all vertices of the tree white.

 

在树上求最小的染色次数使得全树为一个颜色。

求出缩点后的树的直径，除以二上取整即可。

#include <bits/stdc++.h>
using namespace std;

const int N = 500005;

int n;
int cnt;
int c[N];
int bel[N];
int dis[N];
queue<int> que;
vector<int> to[N];
vector<int> TO[N];

void dfs(int u, int f)
{    
    bel[u] = cnt;
    
    for (auto v : to[u])
        if (c[v] == c[u])
            if (v != f)dfs(v, u);
}

signed main(void)
{
    cin >> n;
    
    for (int i = 1; i <= n; ++i)
        cin >> c[i];
    
    for (int i = 1; i < n; ++i)
    {
        int x, y; cin >> x >> y;
        to[x].push_back(y);
        to[y].push_back(x);
    }
    
    for (int i = 1; i <= n; ++i)
        if (!bel[i])++cnt, dfs(i, -1);
        
    for (int i = 1; i <= n; ++i)
    {
        int u = bel[i];
        for (auto j : to[i])
        {
            int v = bel[j];
            if (u != v)
            {
                TO[u].push_back(v);
                TO[v].push_back(u);
            }
        }
    }
    
    memset(dis, -1, sizeof(dis));
    
    dis[1] = 0, que.push(1);
    
    while (!que.empty())
    {
        int top = que.front(); que.pop();
        for (auto v : TO[top])if (dis[v] == -1)
            dis[v] = dis[top] + 1, que.push(v);
    }
    
    int s = 1; 
    for (int i = 2; i <= cnt; ++i)
        if (dis[i] > dis[s])s = i;
        
    memset(dis, -1, sizeof(dis));
    
    dis[s] = 0, que.push(s);
    
    while (!que.empty())
    {
        int top = que.front(); que.pop();
        for (auto v : TO[top])if (dis[v] == -1)
            dis[v] = dis[top] + 1, que.push(v);
    }
    
    int t = 1; 
    for (int i = 2; i <= cnt; ++i)
        if (dis[i] > dis[t])t = i;
        
    cout << (dis[t] + 1) / 2 << endl;
}

 

 

后记：貌似这次CF的题都很友（水）好（水）。

 

@Author: YouSiki