图灵机之雕虫小技

之前写了一篇文章，家里狗狗是否图灵完备？，得出结论，能进行程序计算的一定是图灵完备的，图灵完备的不一定能进行程序计算。

这个结论，不严谨，后来我一直在思考。如果这个问题想清楚了，可能未来对人工智能的重大突破，都来源于对图灵停机问题的深入理解。

我们下面再次从小虫的角度来理解一下图灵机模型、图灵机计算、模拟、计算等问题。

 

原文首发于我的公众号：优前程，点击链接跳转

图灵机之雕虫小技

图灵机

 

 

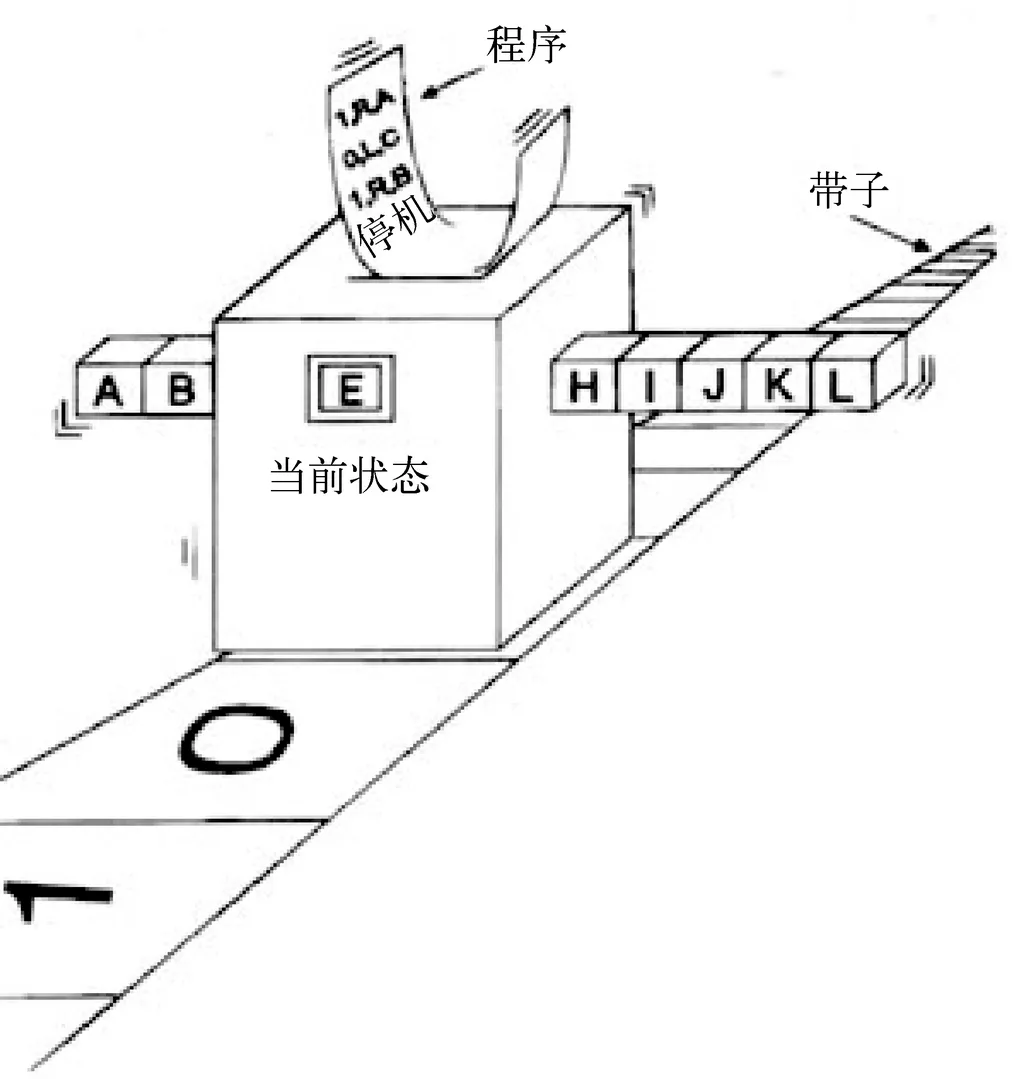
这个装置由下面几个部分组成：一条无限长的纸带；一个读写头（中间那个大盒子）；内部状态（盒子上的方块，比如A、B、D、E）；还有一个程序对这个盒子进行控制。这个装置就是根据程序的命令及其内部状态进行磁带的读写和移动。

它工作的时候是这样的：从读写头在纸带上读出一个方格的信息，并且根据它当前的内部状态开始在程序表中查找对应的指令，然后得出一个输出动作，也就是往纸带上写信息，还是移动读写头到下一个方格。程序也会告诉它下一时刻内部状态转移到哪一个。

具体的程序就是一个列表，也叫作规则表或指令表。

因此，图灵机只要根据每一时刻读写头读到的信息和当前的内部状态进行查表，就可以确定它下一时刻的内部状态和输出动作了。

图灵机就是这么简单！不可思议吧？而只要你修改它的程序（也就是上面的规则表），它就可以为你做计算机能够完成的任何工作。因此可以说，图灵机就是一个最简单的计算机模型！

也许，你会觉得图灵机模型太简单，怎么可能完成计算机的复杂任务呢？问题的关键是如何理解这个模型。

理解图灵机模型

首先我们现实世界给图灵机建模。我们假设纸袋上有一只小虫，它思想很简单，只会根据纸带颜色，决定当前的行动。

小虫1.0

目前给它的指令是，看到黑色格子，前移一格；看到白色格子，后移一格。

• 黑色 前移
• 白色 后移

如下图

 

小虫会在后面两个格子之间永远循环下去……

无论怎样，小虫比起真实世界中的虫子来说，有一个致命的弱点：那就是如果你给它固定的输入信息，它就会给你固定的输出信息！因为程序是固定的，每当黑色信息输入的时候，无论如何小虫都仅仅前移一个方格，而不会做出其他的反应。它似乎真的是机械的！

小虫2.0

上面的小虫，没有内部状态，就是说没脑子，不能做判断，我们现在给它内部状态，升级一下程序。

输入	当前内部状态	输出	下一时刻的内部状态
黑	饥饿	涂白	吃饱
黑	吃饱	后移	饥饿
白	饥饿	涂黑	饥饿
白	吃饱	前移	吃饱

这里就比较绕了，比1.0复杂很多。你不仅需要指定每一种输入情况下小虫应该采取的动作，而且还要指定在每种输入和内部状态的组合情况下小虫应该怎样行动。

第一步：

 

 

第二步：

 

 

第三步：

 

 

第四步：

 

 

第五步：

 

 

第六步：

 

第七步：

 

第八步：

 

这时候的情况已经跟第四步的完全一样了，因而小虫会完全重复五、六、七、八步的动作，并永远循环下去。最后的黑色方格似乎是一个门槛，小虫无论如何也跨越不过去了。

小虫的行为比以前的程序复杂了一些。尽管从长期来看，它最后仍然会落入机械的循环或者无休止的重复。然而这与前面的程序从本质上已经完全不同了，因为当你给小虫输入白色信息的时候，它的反应是你“不能预测”的。它有可能涂黑方格也有可能前移一个格。当然前提是你不能打开小虫看到它的内部结构，也不能知道它的程序，那么你所看到的就是一个“不能预测”的满地乱爬的小虫。如果小虫的内部状态数再增多呢？那么它的行为会更加地“不可预测”。

说到这里，你可能对于“小虫的行为不可预测”这句话持反对意见。因为所有可能的输入状态是固定的，所有的内部状态无论多少也是固定的，那么小虫所有可能的行为就应该是有限的。然而，不要忘记纸带的长度是无限的，虽然每个具体的输入可能只有0和1两种状态，然而这些0和1的输入组合却是无限的。

退一步说，输入纸带的情况是有限的（你可以理解为01组合经过若干长度就会出现循环，比如011011011…），那么我们的小虫最终会不会必然陷入到无休止的循环中呢？答案是肯定的，因为这个时候输入的组合数乘以内部状态总数是一个有限的数值，因而小虫必然会在某时开始重复。

无论哪种情况，似乎你都可以通过某种聪明的“数学”判断小虫是否会循环以及在什么时候循环。也就是说，通过你那聪明的数学，只要看看小虫的程序，而不用执行它就能够预言小虫在多少步之后必然会“傻傻地”重复以前的动作。这样一来，那可真是名副其实的“雕虫小技”了。然而真的是这样吗？这种判定小虫傻傻循环的一般定理或程序存在吗？这个问题留待我们后面进行讨论。

好了，如果你已经彻底搞懂了我们的小虫是怎么工作的，那么你已经明白了图灵机的工作原理。因为从本质上讲，最后的小虫模型就是一个图灵机。

如何理解图灵机模型

刚才用小虫说明了图灵机的工作原理，相信你的第一个反应就是，这样的模型太简单了！它根本说明不了现实世界中的任何问题！下面，我就要试图说服你，图灵机这个模型是伟大的。

首先，我想说的是，其实我们每一个会决策、会思考的人就可以被抽象地看成一台图灵机。

小虫模型本质是：输入集合、输出集合、内部状态、固定的程序。就是这四样东西抓住了小虫信息处理的根本，也就是图灵机模型。

IPO模型

IPO ——input，progress，output。

再抽象一点，这就是个IPO模型。我们大脑就是这样的，看到美丽的景色，脑袋里面遣词造句，输出优美的文字；看到小孩跌倒，生出同情心，帮助小孩站起来；用手触摸水，太烫，兑冷水……

 

 

五官六感输入信息，大脑有内部状态进行处理，行动作出调整和改变（即输出）。

 

再回到开头，说的狗狗，也是一样的，所有动物都是这样的，又如前文比喻的小虫。

包括，记忆（内部状态），学习（程序的改变或升级），情绪（内部状态，情绪好和坏的时候，对应的不同规则的反应）。人的行为反应不固定，并非是机械化的。

我们也可以争辩，无论神经元如何传递信息、变化状态的规律都是固定的，可以被程序化的。那么脑作为神经元的整体，它的运作必然也要遵循固定的规则也就是程序了。如果是这样，正如图灵相信的，人脑也不会超越图灵机这个模型，所以，人工智能也必然是可能的。然而，我认为这个问题的答案很有可能没有这么简单。

无论如何，我相信你已经能够体会到了图灵机模型实际上是非常强有力的。数学家们早已经提出了邱奇-图灵论题以概括图灵机的计算能力，任何可计算过程都可以用图灵机来模拟。这是一个论题而非定理，因为它实际上是对可计算过程的定义，而非证明。但迄今为止，人们尚未发现一个可以视为计算的过程是图灵机不能模拟的，这就是图灵机模型的厉害之处了。

计算

前文讲过IPO模型，input 和output好理解，那我们再来看看progress，我们可以将其理解为“计算”。

如何理解？

如果我们把一切都看作信息，那么广义上讲，计算就是对信息的变换。你会发现，其实自然界充满了计算。如果我们把一个小球扔到地上，小球又弹起来了，那么大地就完成了一次对小球的计算。因为你完全可以把小球的运动都抽象成信息，它无非是一些位置、速度、形状等能用信息描述的东西，而大地把小球弹起来无非是对小球的这些信息进行了某种变换，因而大地就完成了一次计算。你可以把整个大地看作一个系统，而扔下去的小球是对这个系统的输入，那么弹回来的小球就是该系统的输出，因而也可以说，计算就是某个系统完成了一次从输入到输出的变换。

如果这样理解，你会发现，世间万物，到处都是“计算”。

计算的组合

更有意思的是，我们可以把若干个计算系统进行合并，构成更大的计算系统。比如还是那个小球，如果往地上放了一个跷跷板，小球掉到地上会弹起这个跷跷板的另一端，而跷跷板的另一端可能还是一个小球，于是这个弹起的小球又会砸向另一个跷跷板……

我们自然可以通过组合若干图灵机完成更大更多的计算，如果把一个图灵机对纸带信息变换的结果输入给另一台图灵机，然后再输入给别的图灵机……这就是把计算进行了组合。也许你还在为前面说的无限多的内部状态和无限复杂的程序而苦恼，那么现在不难明白，实际上我们并不需要写出无限复杂的程序列表，仅仅将这些图灵机组合到一起就可以产生复杂的行为了。

有了图灵机的组合，我们就能够从最简单的图灵机开始构造复杂的图灵机。那么最简单的图灵机是什么呢？我们知道最简单的信息就是0和1，最简单的计算就是对0或1进行的布尔运算。而布尔运算本质上其实就三种：与、或、非。从最简单的逻辑运算操作最简单的二进制信息出发，我们其实可以构造任意的图灵机。这点不难理解：任何图灵机都可以把输入、输出信息进行01编码，任何一个变换也可以最终分解为对01编码的变换，而对01编码的所有计算都可分解成前面说的三种运算。也许，现在你明白了为什么研究计算机的人都要去研究基本的布尔电路，cpu基本组成原理也是这个。奥秘就在于，用布尔电路可以组合出任意的图灵机。

征服无限的方法

我们会想小时候学加法，当理解了1+1=2原理了，几乎十以内加法都可以做，理解了进位，就可以做几百加几千的运算了。这个是小学四年级就会的，我们并不是将所有的加法都背下来的哦，我们是知道了相加的规则和进位的规则，这样多么复杂的两个数字相加，我们都可以求出解。

这就是归纳方法。

之前看到过一个问题，如果人类将要灭亡，最后留给后人一张纸，上面写什么？其中就有1+1=2。数学之美：关于两条直线的平行和相交

 

 

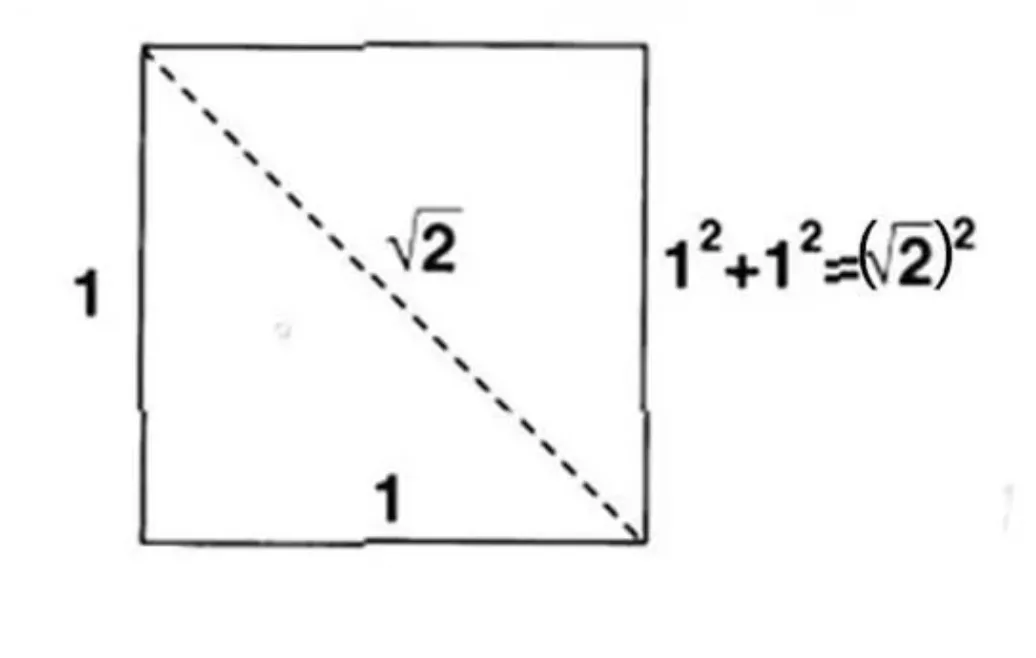
有了加法，就推出减法，有了减法，就自然会有“负数”概念；为了快速算加法，就有了乘法；有了乘法，就有了平方；有了平方，就会有人想到开方；当有古希腊好事者想对2开方，就有了引发第一次数学危机的无理数……

这就是人类数学大厦地基的一部分。如果我们能找出一些归纳方法，编出能让机器进行归纳的程序，然后机器能自己进行归纳学习，我们再也不用给它编制程序和规则了。这正是人工智能的终极目标。

归纳

上文讲了归纳的重要性，就是什么叫“开悟”。不管是看武侠小说，还是现实生活中说谁聪明。除了记忆力好以外，更重要的是，他能从一些原来输入的一些招式中，变幻出新的招式，从理解了1到能演绎出100种打法。

就像知道了11+17=28，几千上百个加法题，你都可以解开一样。

回到计算机，如果计算机能自动归纳，也就意味着我们可以为归纳方法编写一段程序P。这个程序可以理解为输入的是一些特殊的数对，输出的是能够生成这些数对的程序。也就是说输入具体的“招术”，输出的是这些“招术”的一般规律。如果程序P真的可以归纳，那么P就必然可以归纳出所有的规律。

大概是这样:

输入：[1,a],[3,b],[4,c],[7,d]…… 

获取归纳程序：P

把这1000个特殊情况输入到P中，那么P就应该能够产生这些对子的共性，也就是P自己这个程序了。换句话说，程序P产生了它自己，P自己把自己给归纳出来了。这似乎陷入了怪圈之中！另外，我们人类设计出来P，如果P可以归纳所有的规律，那么P能否归纳出“人归纳P”本身这个规律呢？仍然是怪圈问题！这样的问题似乎还有很多。

事实上，索洛莫诺夫（Solomonoff）很早就提出了通用归纳（universal reduction）模型，并对这个问题给出了明确的回答：虽然我们可以数学地写出通用归纳模型，但它却是不可计算的，也就是程序P并不存在，这与后面讨论的图灵停机程序有关。

模拟

什么是模拟？又是一个基本的问题，阿尔伯特·爱因斯坦说过，越是基本的概念就越是难以刻画清楚。模拟这个概念就是一个很难说清的问题。

比如，你跟孩子做了个鬼脸😜，她也学你做了一摸一样的鬼脸。你可以说她对你进行了模拟。得一摸一样才行，如果你做鬼脸，她摇头就不是模拟了。

因而，模拟的关键是对应。如果集合A中的元素可以完全对应B中的元素，那么A就可以模拟B。

仍然是以做鬼脸为例，假如这次你做出的鬼脸以及动作没有被他立即模仿而是被他用某种符号语言记录到了日记本上，比如“X年X月X日，疯子XX冲我做了一个鬼脸：他伸出了左手食指放到了右眼下面往下拉他脸上的肉，并且吐出了他长长的舌头！”。过了N多天后，你的这位朋友掏出了日记本，按照上面的描述冲着大家做了这个鬼脸。很显然他仍然模拟了你当时的动作。

那么，你朋友日记本上的那段描述是不是对你鬼脸动作的模拟呢？答案似乎是否，因为这段文字跟你没有半点相像。然而你的朋友正是根据这段描述才做出了对鬼脸动作的模拟。也就是说，他把那段文字翻译成了他的动作，而他这个动作就是对你的模拟。这个翻译的过程很显然就是某种信息的变换，我们完全可以把它理解为一个计算的过程，也就是可以用图灵机来实现的算法过程。所以，我们说日记本上的那段指令也构成了对你鬼脸动作的模拟，原因是这些信息也与你的鬼脸动作构成了对应。

 

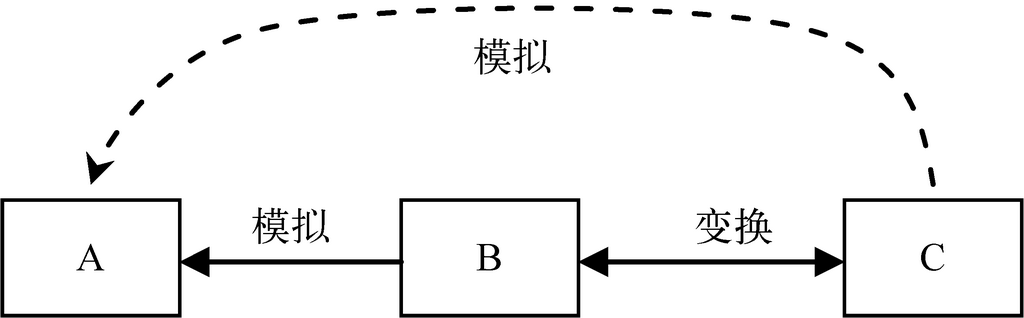
图中A是你的鬼脸动作，B是你朋友做出来的鬼脸动作，C是日记本上的描述。你朋友的动作B模拟了你的动作A，而B的动作信息是通过执行C上的描述得到的，也就是说，存在着一个从C到B的信息变换。这样我们认为C也对A进行了模拟。

图灵机的模拟

下面来考虑图灵机之间的模拟。按照前面的定义，一台图灵机包括输入集合I、输出集合O、内部状态集合S、程序规则表T四个要素。那么，如果两个图灵机之间的这些元素都存在刚才说的对应关系，就认为这两个图灵机可以相互模拟了。然而图灵机的功能是完成对输入信息进行变换得到输出信息的计算。我们关心的也仅仅是输入输出之间的对应关系。因而一台图灵机A如果要模拟B，并不一定要模拟B中的所有输入、输出、内部状态、程序规则表这些元素，而只要在给定输入信息的时候能够模拟B的输出信息就可以了。

因此，我们可以用下图表示图灵机之间的模拟。

 

 

 

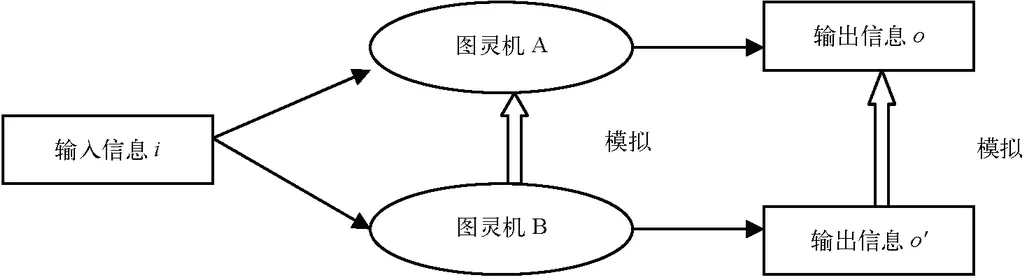
也就是说，在给定相同输入信息的情况下，只要输出信息 o' 能够模拟信息 o，也就认为B模拟了A。而信息 o' 对信息 o 的模拟又符合我们上面对一般集合之间模拟的定义。也就是说，如果存在另外一台图灵机能够把信息 o' 计算并映射成信息 o，就认为 o' 模拟了 o。说白了也就是 o' 可以与 o 不一样，但是只要你能用一个图灵机把 o' 经过一系列运算变换到相同的 o，就认为 o' 模拟了 o。因而也就是图灵机B模拟了图灵机A。

进一步地，我们可以假设A和B输入的信息也不一样，一个是 i，另一个是 i'，那么如果 i 和 i' 之间也存在着模拟对应关系的话，我们仍然认为B可以模拟A，

计算等价性

讲了这么多关于模拟的知识有什么用呢？模拟的一个关键作用就是阐明什么是等价的。比如为了完成加法运算，你写了一段程序，我也写了一段程序，虽然我们两个的程序可能完全不一样，然而只要我们两个程序之间能够相互模拟，也就是说只要给定两个数，我们都能正确地一模一样地算出它们的和，那么我们两个程序就是等价的。

比如做加法，不管是js写，还是python、c、c++、go，写法不同，结果都能进行加法计算。那么他们计算就是等价的。所以，加法是永恒而独立的，只是计算实现的方式不一样。

看！我们在宇宙中找到某种永恒性了，这种永恒性反映了宇宙规律中某种本质上的美。计算等价性就和能量守恒定律一样具有这种高级的对称性，我甚至觉得计算等价性要比能量守恒定律更加深刻。因为无论如何能量守恒定律仍然刻画了物理系统的某种属性，而计算等价性刻画的则是非常广泛的信息系统之间的对称性，而一切系统都可以被抽象为信息系统，甚至是物质世界。所以，计算等价性是跨越所有系统之间的某种高级对称的、永恒的、美的东西。

理解了这一点，我相信你也能理解为什么说，任何计算是图灵机的翻版这一观点了。

意义

考虑下面三句话：

• i love you;
• 我爱你；
• 月が绮丽ですね（今晚月色很美，日本我爱你的含蓄表达）；

你跟美国人说，i love you，对中国人说，我爱你，对日本对象说月が绮丽ですね，他们都会理解你说的什么，也许还会一阵脸红心跳。

显然，这三句话说法不同，但是意义是一样的。

如果将此场景设想成图灵机，那么三个人不同的输入，输出是相同的，就是前文说的“计算等价性”。

我们不难得出结论：所谓语言的意义，就是执行这个语言系统的计算等价性。

我们目前都是如何计算语言的等价性的呢？翻译。

然而，当不存在从一种语言到另外一种语言的翻译的时候，我们也并不能断定某一个符号序列对于固定的图灵机是否有意义。例如，我们虽然不能明白鸟叫是什么含义，但并不能否认它们的叫声可能有意义，因为只有鸟自己才能明白叫声的含义。

万能图灵机

前面已经讲述了模拟的概念，那么自然会产生这样一个问题：是否存在一台图灵机能够模拟所有其他的图灵机呢？答案是存在的。这种能够模拟其他所有图灵机的图灵机叫作通用图灵机（Universal Turing Machine），也就是我所说的“万能图灵机”。我之所以这么称呼它，是因为这种机器在图灵计算这个范畴内是万能的。

万能图灵机会怎样工作呢？假如我把信息 x 输入到了图灵机M 中，M就能计算出一个结果 o。那么如果我把 x 和M的信息都输入给万能图灵机，那么它也会输出 o，也就是万能图灵机可以模拟任何一台特殊的图灵机。这样的话我们仅仅通过改变输入 x 和M的值就能“改变”万能图灵机的程序规则了，因而也可以认为万能图灵机就是可以任意编程的。这里的“改变”两个字加上了引号，是因为事实上任何图灵机在诞生之后就不能改变规则了，因而虽然看上去改变了万能图灵机的规则，其实根本没有改变。

如果一台图灵机的编码是M，它读入的信息是x，这样只要把M和 x 用“.”号隔开，分开作为数据输入到万能图灵机中，运用特殊的算法，这个万能的机器就能得出对M计算 x 的模拟结果了。事实上可以由定理证明万能图灵机对于任意的编码都是存在的，在这里我们就不叙述证明过程了。

自食其尾

既然万能图灵机能够模拟任何一台图灵机的动作，那么它能不能模拟它自己呢？答案是肯定的。我们首先看到万能图灵机也是图灵机，也有固定的输入、输出、状态的集合、固定的程序，因而它也能被编码。于是我们就可以把它自己的编码信息输入给它自己。这就好像一条蛇咬到了自己的尾巴，自食其尾就会产生怪圈，虽然我们现在还没有看到任何不好的征兆。

有了万能图灵机，还能得到很多有趣的结论，比如假设有一大群图灵机，让它们随机地相互碰撞，当碰到一块的时候，一个图灵机可以读入另一个图灵机的编码，并且修改这台图灵机的编码。那么这样一个图灵机“汤”中会产生什么呢？美国圣塔菲研究所的方塔纳（Walter Fontana）完成了这个实验，并得出了惊人的结论：在这样的系统中会诞生自我维护的类似生命的复杂组织，而且这些组织能进一步联合起来构成更大的组织！

停机问题

尽管图灵机如此强大，它也有解决不了的问题。例如，一个著名的不可解问题就是图灵停机问题。

死循环

还记得我们前面提到的可怜的“小虫”吗？当时我们就提出来一个问题：会不会存在某种聪明的算法P，只要检查一下小虫的程序和纸带信息，而不用执行它，就能够让我们预言小虫是否会陷入死循环，无休止地重复前面的动作？

可惜的是，这种判断任意程序作用到任意数据上是否停机的程序P并不存在。我们可以给出一个证明。

在进行正式讨论之前，我们先来看一个非常简单的猜硬币游戏。

假如我两只手中有一个攥着一枚硬币，另一个什么都没有，然后让你猜硬币在哪一个手中？于是你告诉我左手。这时候我不会把手张开，而是背过身去做一番手脚，然后把手伸过来，张开手！哈，你错了吧，硬币在右手中！

大概傻子都能看出来我的伎俩之所在。不用说，采用这种方法我保证百战百胜。因为我总是等你说出来是哪只手有硬币之后再动态地改变我的策略。所以，改变之后的状态已经不是你猜的了。

大概你会觉得不可思议：其实图灵停机问题的证明就与这个游戏有点类似。

你想猜对我的硬币，就必须告诉我你的答案是左手还是右手，然而问题是我总能根据你给出的答案进行动态调整，让你永远也猜不对！停机问题也是如此，我总能根据你的程序P来构造P判定不出来的问题Q，我总会赢！很简单，因为你总要在我之前构造好P，就相当于你总要先说出硬币在哪个手中。

意味着什么

我们已经看到了，的确存在着一些我们人类能构造出来而图灵机不能解的问题。我们知道图灵机不能解的问题也就是一切计算机都不能解的问题，因而这类问题是不可计算的。因此，必然存在着计算机的极限。实际上，根据我们前面叙述的计算等价性原理，很多问题都可以被归结为图灵停机问题，也就是说图灵停机问题揭示了宇宙中的某种共性，所有计算机不能解决的问题从本质上讲都和图灵停机问题是计算等价的。比如在最开始我们提到的希尔伯特第十问题，就是一个典型的不可计算问题。还有很多问题是不可计算的，尤其是那些涉及计算所有程序的程序。比如是否存在一个程序能够检查所有的计算机程序会不会出错，这是一个非常实际的问题，然而这样的程序仍然是不存在的，其实可以证明这个问题和图灵停机问题实质上是一样的。于是我们的梦想又破灭了。

图灵停机问题也和复杂系统的不可预测性有关。我们总希望能够预测出复杂系统的运行结果。那么能不能发明一种聪明的程序，输入某个复杂系统的规则，输出的是这些规则运行的结果呢？从原则上讲，这种事情是不可能的。它也和图灵停机问题等价。因而，我们得出来的结论就是：要想弄清楚某个复杂系统运行的结果，唯一的办法就是让这样的系统实际运作，没有任何一种计算机算法能够事先给出这个系统的运行结果。但这并不是说不存在一个特定的程序能够预测某个或者某类复杂系统的结果。那么这种特定的程序怎么得到呢？显然需要我们人为地编程得到。也就是说存在着某些机器做不了而人能做的事情。这对人工智能的崇拜者来说似乎是沉重的打击。

人工智能真的是不可能的吗？彭罗斯曾经写过一本科普名著《皇帝新脑》来论证人工智能的不可能性。书中所运用的方法就是我们上面的逻辑。因为对于任何一个人工智能程序来说，总存在着它解决不了的问题。但是似乎我们人类却不受这种限制，我们总是能够发现一个程序是否有死循环，总是能够找到对某类复杂系统预测的方法，并且我们还能构造出图灵停机这样的问题。

超越图灵机

我们仍然以那个猜硬币的游戏为例来说明。

在进行了几轮猜硬币的游戏之后，你已经很恼火了，认为这样的游戏不公平。于是你想了一个妙招来对付我：每当我让你说硬币在哪只手中时，你先胡乱说一个答案，比如左手。于是我会根据你的答案进行动态调整，把硬币放到了右手中。这个时候你赶紧抢着说：不对，我猜你的硬币在右手！我没办法只能再次调整策略把硬币放到了左手中。你又赶快说：是在左手！……就是这样，你也学会了我的方法，根据我的策略不断调整你的策略从而让我不可能赢你。能不能把这种方法用到超越图灵停机问题呢？

前面我们已经看到了类似这样的过程。如你写出了一个程序P能够判断所有程序是否停机，那么我就能构造一个你的程序判断不了的程序Q。这时你又根据我的程序Q构造了新的程序P'，然而我又能构造一个程序Q'，仍然让你的程序P' 判断不了。但是你没有结束，又构造了新的程序P''，于是我又构造了Q''……

乍一看，似乎这个过程并不能说明任何问题。原因很简单，我要求的是构造一个固定的程序P判断出所有程序是否停机，而你给我的并不是一个具体的实实在在的程序，而是一个不断变化、捉摸不定、虚无飘渺的程序序列，并且你的这些总在变化的程序序列总是要根据我构造的程序才会确定改变。

首先值得肯定的一点是，运用这种方法，你的确能够超越图灵计算了，只要反复不停地变换你的程序，就不可能找出它不能解的问题。然而，另一方面又会让我们很失望：这样的变换过程并不能给出一个实实在在的程序来。我们拥有的仅仅是不断改变的程序序列，而不是一个实际存在的程序。

这正是问题的关键所在：要想彻底超越图灵计算的限制，我们必须放弃程序的实在性。也就是说程序每时每刻都要变化。那么这样一个不断变化得不是它自己的怪东西存在吗？

几千年的人类科学一直在研究实实在在的东西。无论是原子、分子还是计算机程序，它们必须是一个实实在在存在的个体，在这种前提下科学才能够对它进行研究。如果当我们研究它的时候，它已经变得不是它自己了，那么科学就对它无能为力了。然而，我不禁要提出这样的问题：真的一切都是固定不变地存在着的吗？有没有某种东西在每一时刻都在变得不是它自己呢？

这似乎是一个古老的哲学问题了。记得赫拉克利特就曾经提到过：一个人不能两次踏入同一条河流。《悉达多》里面有描述到，我想他说的正是这样的问题：因为河流在每时每刻都不再是它自己了。河流是一大群流动的水滴构成的整体，这些水滴每时每刻都在不停地运动、流逝，因而当你两次踏入这条河的时候，所有的水滴可能都不一样了，那么我们怎么能说这些水滴构成的整体还是同一条河呢？

再考虑我们人自己。你很可能拿着一个3岁时的照片兴奋地对你的朋友说：“看，我3岁的时候多可爱呀！”然而你这句话意味着什么呢？意味着照片反映的3岁的你和现在的你是同一个个体。然而，3岁的你和现在的你是多么不同呀！我们知道，你无疑就是一大堆细胞构成的整体。而基本生理学知识告诉我们，人体的所有细胞每隔大约4年就会因为新陈代谢的作用全部更新一遍，也就是说，你的细胞全被调了包了，更何况3岁的你和现在的你差了多少个4年呀？那凭什么说那个3岁的你就是现在的你呢？

这个问题看似玄学，不过我认为现在我们的确应该认真对待该问题了。尽管从分析的角度来说，3岁的你和现在的你的确不是一个个体，然而常识告诉我们，这两个你的确都是同一个人。那就意味着，你这个个体并不是一些一成不变的固定的细胞，而是一个每时每刻都在变化和更新的一大堆细胞组成的构形。这个构形在每时每刻都要利用更新的一大堆细胞去维持自己的存在。和我们前面叙述的超越图灵机的讨论结合起来就会发现，人和赫拉克利特的河流这种东西刚好就满足超越图灵计算的要求。也就是说人和赫拉克利特的河流在每时每刻都在不停地更新自己从而变得不是它自己了。那么很有可能，某一种做类似变化的个体的变化规律就是不停超越它自己的图灵停机程序，这样的虚幻的个体就真的能够超越图灵计算了。

总结前面的讨论，我们不难得出结论，一个写出就不再变化的固死的程序不可能超越图灵计算的限制，然而如果一个程序每时每刻都变化得不是它自己了，那么这个程序就能够超越图灵计算。联系到人这个个体，我们就能得到：因为每时每刻的人都已经由于细胞的变化而变得不再是它自己了，所以人是超越图灵计算的。还记得我在前面提到的一个问题吗：人脑的信息处理过程能不能被表示成固定的程序呢？我这里的答案就是否定的，也就是说人脑信息处理的过程并不是一个固定的程序。如何制造真正的人工智能呢？我们的答案就是：一个能不断改变自己的程序，而且这种改变也不是一个固定的程序。

所以，人只有是不断学习，进化，变化的，才是真正的智能。否则25岁死，75岁才埋，就是接近真实的。