一、逢“几”中奖
逢“几”中奖,即通过预估抽奖人数和奖品数来判断,“几”=(抽奖人数/奖品数)*N。这是一种最简单抽奖算法,适合抽奖人数众多,而且互相无联系的情况。如今大为流行的微博转发得奖就常常使用这种算法,即根据转发次数来决定奖品归属,透明而且具有激励性。
当然这个“几”也不单只次数,还可能是时间,逢某个时间点就可以抽中,不过这种方案可能产生无人中奖和很多人中奖的情况,时间点的安排很关键!这个时间点一旦公布出去,那就是秒杀,霍霍。。
逢“几”中奖有很多弊端,但是非常简单,很容易实现,被很多抽奖活动所采用,有些会公布抽奖规则,激励抽奖,有些则不会公布,其实后台运行的可能也是这个算法,简单高效又不失公平。在信息不透明的情况下,鬼知道你是第几个抽奖的,哈哈。。
二、概率抽奖
所谓概率抽奖是最容易想到的抽奖算法了,这个概率可以是一成不变的,也可以是一直在变化调整的,最难的是采用多大的概率,何种情况下采用何种概率。这个也没有什么通用的方案,不同的应用场景,所用的概率算法不同。下面介绍一种算法,根据奖品的过期日期来计算它当前时间的中奖率,当时间逐渐接近奖品过期时间时,中奖概率会逐渐发生变化,如果设为1表示线性衰减,2为平方衰减,以此类推。
importjava.util.Date; importjava.util.Random; publicclass LotteryTool { private double factor; private double probability; private Random rand; private LotteryTool(double probability, long expireTime, int reduce){ this.factor = (double) System.currentTimeMillis() / expireTime; this.probability = probability * Math.pow(factor, reduce); this.rand = new Random(System.currentTimeMillis()); } public static LotteryTool getInstance(double probability, longexpireTime, int reduce) { return new LotteryTool(probability, expireTime, reduce); } public boolean isLucky(long expected) { long token = generateLong(); expected = expected % (int) (1 / probability); if (expected == token) { return true; } return false; }
三、依赖不可控的物理随机数
什么意思呢,先看个图,看完你就知道了

明白了吧,呵呵,这就是现如今灰常流行的一种抽奖算法,绝对公平、绝对透明、绝对木有暗箱(除非偷偷给你换了抽奖号码)!但是这种方法唯一的缺点是无法实时抽奖,只能事后抽奖。也就是只能拿个抽奖号等着上帝的眷顾,阿门。。。
例如游戏中打败一个boss,会掉落下面其中一个物品,而每个物品都有一定概率: 1. 靴子 20% 2. 披风 25% 3. 饰品 10% 4. 双手剑 5% 5. 金币袋 40% 现在的问题就是如何根据概率掉落一个物品给玩家。
一. 一般算法:生成一个列表,分成几个区间,例如列表长度100,1-20是靴子的区间,21-45是披风的区间等,然后随机从100取出一个数,看落在哪个区间。算法时间复杂度:预处理O(MN),随机数生成O(1),空间复杂度O(MN),其中N代表物品种类,M则由最低概率决定。
二、离散算法:也就是上面的改进,竟然1-20都是靴子,21-45都是披风,那抽象成小于等于20的是靴子,大于20且小于等于45是披风,就变成几个点[20,45,55,60,100],然后也是从1到99随机取一个数R,按顺序在这些点进行比较,知道找到第一个比R大的数的下标,比一般算法减少占用空间,还可以采用二分法找出R,这样,预处理O(N),随机数生成O(logN),空间复杂度O(N)。 请点击查看详细:http://www.cnblogs.com/miloyip/archive/2010/04/21/1717109.html
三、Alias Method Alias Method就不太好理解,实现很巧妙,推荐先看看这篇文章:http://www.keithschwarz.com/darts-dice-coins/ 大致意思:把N种可能性拼装成一个方形(整体),分成N列,每列高度为1且最多两种可能性,可能性抽象为某种颜色,即每列最多有两种颜色,且第n列中必有第n种可能性,这里将第n种可能性称为原色。 想象抛出一个硬币,会落在其中一列,并且是落在列上的一种颜色。这样就得到两个数组:一个记录落在原色的概率是多少,记为Prob数组,另一个记录列上非原色的颜色名称,记为Alias数组,若该列只有原色则记为null。
之前的例子,为了便于演示换成分数 1. 靴子 20% -> 1/4 2. 披风 25% -> 1/5 3. 饰品 10% -> 1/10 4. 双手剑 5% -> 1/20 5. 金币袋 40% -> 2/5 然后每个都乘以5(使每列高度为1),再拼凑成方形 拼凑原则:每次都从大于等于1的方块分出一小块,与小于1的方块合成高度为1
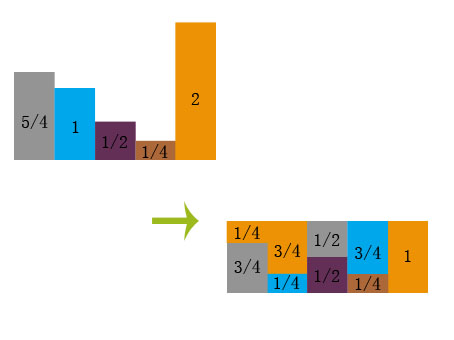
由上图方形可得到两个数组: Prob: [3/4, 1/4, 1/2, 1/4, 1] Alias: [4, 4, 0, 1, null] (记录非原色的下标)
之后就根据Prob和Alias获取其中一个物品 随机产生一列C,再随机产生一个数R,通过与Prob[C]比较,R较大则返回C,反之返回Alias[C]。
Alias Method 复杂度:预处理O(NlogN),随机数生成O(1),空间复杂度O(2N)



 浙公网安备 33010602011771号
浙公网安备 33010602011771号