LeetCode74 搜索二维矩阵-----二分查找

题目表述

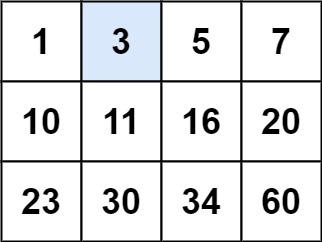
编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

二分查找

• 从题目可以看出，矩阵的每一行是递增的，每行的第一个元素大于前一行的最后一个元素，所以每列也是递增的。

• 对矩阵最后一列的元素进行二分查找，如果等于target直接返回，否则找到一个大于目标值得元素

• 判断当前大于目标值元素所在的行，如果所在等于了矩阵的行数，则说明矩阵中的所有元素都小于target，return false。

• 否则的话二分搜索当前行，找到target则返回。否则返回false。

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int l = 0, r = matrix.length - 1;
        while(l <= r){
            int mid = l + ( r- l) / 2;
            
            if(matrix[mid][matrix[0].length - 1] < target){
                l = mid + 1;
            }else{
                r = mid - 1;
            }
        }
        if(l == matrix.length){
            return false;
        }
        if(matrix[l][matrix[0].length - 1] == target){
            return true;
        }
        int left = 0; int right = matrix[0].length - 1;
        while(left <= right){
            int mid = left + (right - left) / 2;
            if(matrix[l][mid] == target){
                return true;
            }else if(matrix[l][mid] < target){
                left = mid + 1;
            }else{
                right = mid - 1;
            }
        }
        return false;
    }
}

__EOF__

本文作者：Younger
本文链接：https://www.cnblogs.com/youngerwb/p/16184113.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！