LeetCode1609奇偶树-----BFS广度优先搜索

题目表述

如果一棵二叉树满足下述几个条件，则可以称为 奇偶树 ：

• 二叉树根节点所在层下标为 0 ，根的子节点所在层下标为 1 ，根的孙节点所在层下标为 2 ，依此类推。
• 偶数下标 层上的所有节点的值都是 奇 整数，从左到右按顺序 严格递增
• 奇数下标 层上的所有节点的值都是 偶 整数，从左到右按顺序 严格递减

给你二叉树的根节点，如果二叉树为 奇偶树 ，则返回 true ，否则返回 false 。

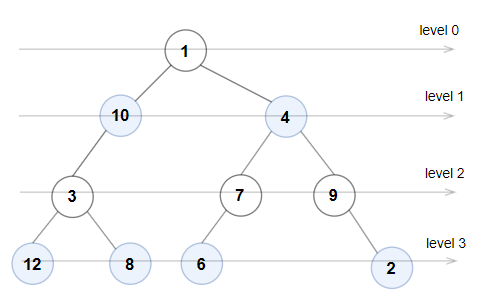
广度优先搜索

使用广度优先搜索遍历每一层的节点，，初始时将根节点加入队列。
在每一轮搜索前，队列中的节点就是同一层的全部节点，将这一层节点的个数记为size，每轮访问只访问size个节点。这样可以确保访问的恰好是同一层的全部节点。

• 判断一棵二叉树是否为奇偶树，需要考虑两个条件，一是节点值的奇偶性，二是节点值的单调性，这两个条件都由层下标的奇偶性决定。因此，需要维护搜索到的层下标，以及对于每一层搜索都需要维护上一个节点值。

• 如果当前层下标是偶数，则要求当前层的所有节点的值都是奇数，且节点值从左到右严格递增。如果遇到节点值是偶数，或者当前节点值小于等于上一个节点值，则二叉树一定不是奇偶树。

• 如果当前层下标是奇数，则要求当前层的所有节点的值都是偶数，且节点值从左到右严格递减。如果遇到节点值是奇数，或者当前节点值大于等于上一个节点值，则二叉树一定不是奇偶树。

• 如果二叉树的所有节点都满足奇偶树的条件，则二叉树是奇偶树。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isEvenOddTree(TreeNode root) {
        Deque<TreeNode> que = new ArrayDeque<>();
        que.add(root);
        int level = 0;
        while(!que.isEmpty()){
            int size = que.size();
            TreeNode pre = que.poll();
            if(pre.left != null) que.add(pre.left);
            if(pre.right != null) que.add(pre.right);
            if(level % 2 == 0){
                if(pre.val % 2 == 0) return false;
                for(int i = 1; i < size; i++){
                    TreeNode tmp = que.poll();
                    if(tmp.left != null) que.add(tmp.left);
                    if(tmp.right != null) que.add(tmp.right);
                    if(tmp.val % 2 == 0 || tmp.val <= pre.val) return false;
                    pre = tmp;
                }
            }else if(level % 2 == 1){
                if(pre.val % 2 == 1) return false;
                for(int i = 1; i < size; i++){
                    TreeNode tmp = que.poll();
                    if(tmp.left != null) que.add(tmp.left);
                    if(tmp.right != null) que.add(tmp.right);
                    if(tmp.val % 2 == 1 || tmp.val >= pre.val) return false;
                    pre = tmp;
                }
            }
            level++;
        }
        return true;
    }
}