冒泡排序&插入排序&其他排序

开始学习第二课，排序相关的知识，以前只接触过冒泡排序，今天还学习了其他的排序方法，主要学习了选择排序、冒泡排序、插入排序，希尔排序和快速排序。

主要排序方法

主要排序方法的解释，其中部分借鉴了百度，主体内容为子龙老师的讲解内容。另外代码中对for循环代码进行优化，以及元素交换做出了新的思路讲解，表示很不错。这里先逐一记录各种排序方法的解释，以及代码实现。在学习排序的过程中，插入排序费了很大力气才理解老师的意思，由于水平有限全程没看到插入的过程，理解插入排序后再理解希尔排序就相对轻松一点，最后的快速排序也是最难理解，花费的时间最多，看完代码才发现老师的代码高度浓缩。

选择排序

它的工作原理有多种解释，这里的理解是其中一种。每一次从待排序的数据中选出最小（或最大）的一个元素，存放在序列的起始位置，然后，再从剩余未排序元素中继续寻找最小（大）元素，然后接着放到已排序序列的后面。以此类推，直到全部待排序的数据元素排完。选择排序是一种不稳定的排序方法，下面自己简单的写了一段代码来记录选择排序，下面这段为初始代码。

 1 import java.util.Scanner;
 2 
 3 public class SelectSort {
 4     /**
 5      * 选择排序，就是每次循环比较都得到一个最值，将其放到指定的位置，然后再循环比较剩余的序列，再次得到最值，放到新的指定位置
 6      * 最后比较完成，完成排序，这就是选择排序。
 7      */
 8 
 9     public static void main(String[] args) {
10         //获取数组
11         Scanner scan = new Scanner(System.in);
12         System.out.println("输入数组长度");
13         int n = scan.nextInt();
14         int[] data = new int[n];
15         System.out.println("开始输入数组具体内容");
16         for (int i = 0; i < n; i++) {
17             data[i] = scan.nextInt();
18         }
19 
20         //排序前
21         System.out.println("排序前");
22         for (int i = 0; i < data.length; i++) {
23             System.out.print(data[i] + " ");
24         }
25         System.out.println();
26 
27         //选择排序
28         for (int i = 0; i < data.length-1; i++) {
29             //外层循环定义下标需要比较的范围，为0到data.length-2
30             for(int j=i+1;j<data.length;j++){
31                 //内层排序，就是拿当前位置的后面元素，一一和它进行比较，如果比它小就进行数组交换，直到比较到数组末尾
32                 //升序排列
33                 if(data[i]>data[j]){
34                     int temp=data[i];
35                     data[i]=data[j];
36                     data[j]=temp;
37                 }
38             }
39         }
40 
41         System.out.println("选择排序后");
42         //重新打印
43         for (int i = 0; i < data.length; i++) {
44             System.out.print(data[i] + " ");
45         }
46 
47     }
48 }

控制台输出结果，可以看出能正常的进行升序排列，选择排序的时间复杂度为O(n^2)，如果数组的长度为n，则上述例子中比较的次数为(n-1)+(n-2)+(n-3)+...+1=n(n-1)/2次，约等于(n^2)/2，但交换次数大于等于n次，因为比较的过程中只要找到比目前小的就进行交换，因此有很多多余的交换，下面会进行修改。

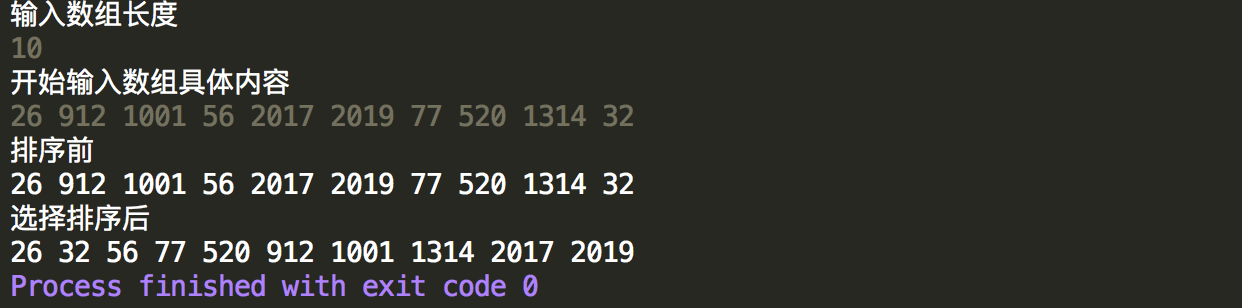
选择排序过程中，如果找到比当前位置数小的，先不进行交换，只记录待交换数的索引值，然后后面的数接着继续和新索引的数比较，如果有找到比它小的继续更新索引直到找到最后的索引。最后将当前位置数和索引位置对应的数进行交换，这才是选择排序的正确理解，前面自己写的可能是错误的，但是也是一种排序的方式。

动画示意如下：

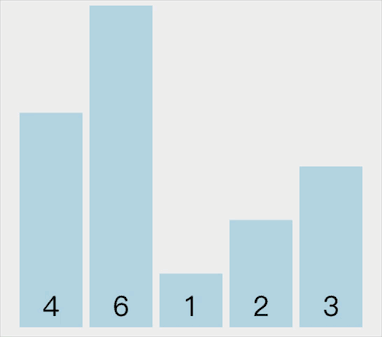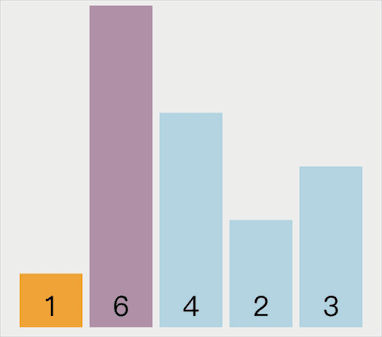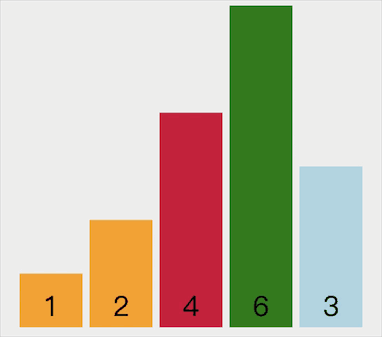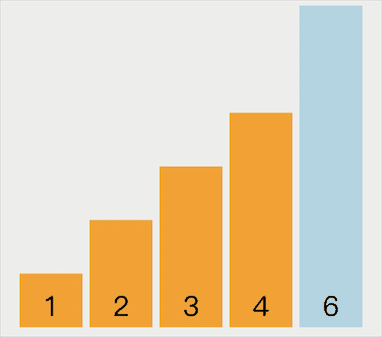
代码实现如下：

 1 import java.util.Scanner;
 2 
 3 public class SelectSortNew {
 4     /**
 5      * 选择排序，就是每次循环比较都得到一个最值，将其放到指定的位置，然后再循环比较剩余的序列，再次得到最值，放到新的指定位置
 6      * 最后比较完成，完成排序，这就是选择排序。
 7      */
 8 
 9     public static void main(String[] args) {
10         //获取数组
11         Scanner scan = new Scanner(System.in);
12         System.out.println("输入数组长度");
13         int n = scan.nextInt();
14         int[] data = new int[n];
15         System.out.println("开始输入数组具体内容");
16         for (int i = 0; i < n; i++) {
17             data[i] = scan.nextInt();
18         }
19 
20         //排序前
21         System.out.println("排序前");
22         for (int i = 0; i < data.length; i++) {
23             System.out.print(data[i] + " ");
24         }
25         System.out.println();
26 
27         //选择排序
28         for (int i = 0; i < data.length; i++) {
29             //外层循环定义下标需要比较的范围，为0到data.length-1
30             //初始下标为i，后面比较后进行下标更新
31             int minIndex=i;
32             for(int j=i+1;j<data.length;j++){
33                 if(data[j]<data[minIndex]){
34                     minIndex=j;
35                 }
36             }
37             //更新完后交换数值
38             if(i!=minIndex){
39                 int temp=data[i];
40                 data[i]=data[minIndex];
41                 data[minIndex]=temp;
42             }
43         }
44 
45         System.out.println("选择排序后");
46         //重新打印
47         for (int i = 0; i < data.length; i++) {
48             System.out.print(data[i] + " ");
49         }
50 
51     }
52 }

修改完代码后，可以看到，选择排序的比较次数为n(n-1)/2，交换次数为n，与冒泡排序有相同的比较次数，但是交换次数控制到了非常低的水平，与数组的长度成线性关系。

冒泡排序

冒泡排序是任何学习编程的人都会接触的，其排序过程是相邻元素两两进行交换，将最大的元素慢慢移动到最后或者最前面，类似水中冒泡的过程，因此形象的叫做冒泡排序，其主要比较过程如下：

比较相邻的两个元素，如果前面元素比后面元素大，就进行数值交换，直到比较到只有data[0]和data[1]进行比较，从比较的过程可以看出，大的元素交换到后面位置后，比较的范围越来越小。

第1次比较：data[0]和data[1]进行比较，data[1]和data[2]进行比较...data[data.length-2]和data[data.length-1]进行比较。

第2次比较：data[0]和data[1]进行比较，data[1]和data[2]进行比较...data[data.length-3]和data[data.length-2]进行比较。

...

第data.length-2次交换：data[0]和data[1]进行比较。

总结成代码就是如下，其中对for循环进行了优化，写成 for (int i = 0,len=data.length; i < len-1; i++)，正常来说data.length写在第二个位置，但是这样每次循环都要执行一次data.length进行取值，如果写到第一个位置，只需要取一次即可，可以说是一个小小的性能优化。

动画示意如下：

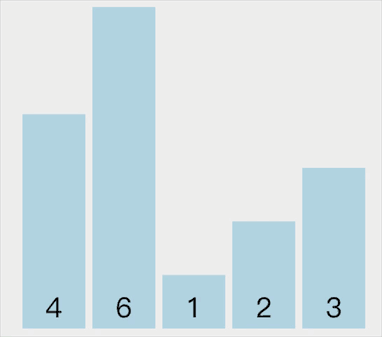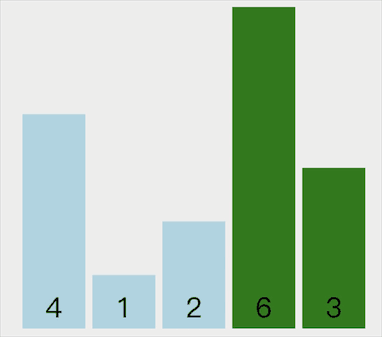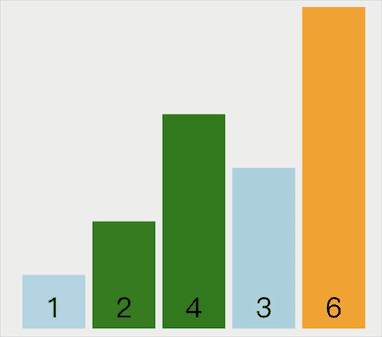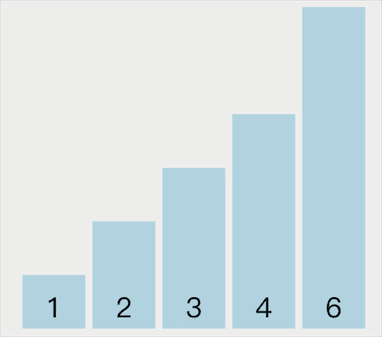
代码实现如下：

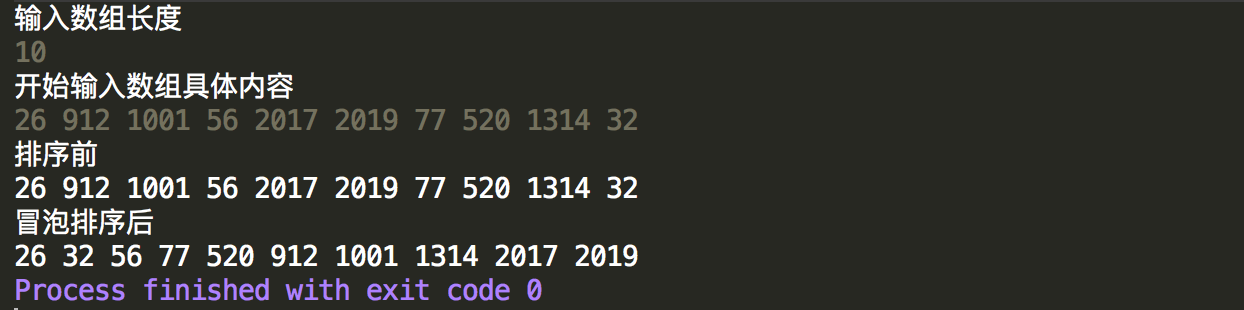
 1 import java.util.Scanner;
 2 
 3 public class BubbleSort {
 4 
 5     public static void main(String[] args) {
 6         /**
 7          * 冒泡排序，主要就是两两比较，这个是最熟悉的算法，没有之一
 8          */
 9 
10         //获取数组
11         Scanner scan = new Scanner(System.in);
12         System.out.println("输入数组长度");
13         int n = scan.nextInt();
14         int[] data = new int[n];
15         System.out.println("开始输入数组具体内容");
16         for (int i = 0; i < n; i++) {
17             data[i] = scan.nextInt();
18         }
19 
20         //排序前
21         System.out.println("排序前");
22         for (int i = 0; i < data.length; i++) {
23             System.out.print(data[i] + " ");
24         }
25         System.out.println();
26 
27         //冒泡排序开始
28         for (int i = 0,len=data.length; i < len-1; i++) {
29             //外层循环为控制内层循环比较的范围，逐一压缩比较范围
30             for (int j = 0; j < len-1-i; j++) {
31                 //第一次冒泡从data[0]-data[1]比较到data[len-2]-data[len-1]
32                 //第二次冒泡从data[0]-data[1]比较到data[len-3]-data[len-2]
33                 //...
34                 //最后一次冒泡比较data[0]-data[1]
35                 if(data[j]>data[j+1]){
36                     data[j]=data[j]+data[j+1];
37                     data[j+1]=data[j]-data[j+1];
38                     data[j]=data[j]-data[j+1];
39                 }
40             }
41         }
42 
43         System.out.println("冒泡排序后");
44         //重新打印
45         for (int i = 0; i < data.length; i++) {
46             System.out.print(data[i] + " ");
47         }
48     }
49 }

控制台输出结果，可以看出能正常的进行升序排列。根据上面排序的过程可以简单的计算一下，第一次比较次数为n-1，随后为n-2，最后只比较1次，因此时间复杂度为(n-1)+(n-2)+...+1=n(n-1)/2，时间复杂度表示为O(n^2)。和选择排序一样，有相同的比较次数，但是交换次数却不止n次，如果每次比较有一半的概率发生交换，则交换的次数为n(n-1)/4，可以看出交换的增长是平方级的。

插入排序

插入排序的基本操作就是将一个数据插入到已经排好序的有序序列中，从而得到一个新的、长度加一的有序序列，插入排序算法适用于少量数据的排序，是一种稳定类型的排序方法。插入排序下面还分为直接插入排序、二分插入排序、链表插入排序和希尔插入排序等，这里先从最基础的直接插入排序开始，以数组4 6 1 2 3为例感受一下插入排序的过程。

第1次插入排序：先取出第一位放到新数组第一位，变成4，这个过程不需要比较。
第2次插入排序：再取出第二位6，跟4进行比较，变成4 6
第3次插入排序：再取出第三位1，跟6比较，发现比它小，交换位置，变成4 1 6，然后1再与4比较，比4小再交换位置，变成1 4 6
第4次插入排序：再取出第四位2，与前面类似，它会逐渐跟6 4 比较，变成 1 2 4 6 ，然后2比1大不再变换位置
第5次插入排序：再取出最后一位3，与前面类似，他会逐一跟4 6进行比较，变成1 2 3 4 6

总结成代码就是如下，其中依然会用来位置交换，除了新建一个临时变量进行交换的方法外，还有直接使用相加的方法，即先将要交换的两个数相加到一起，然后用这个数减去相加的两个数，错位赋值（自己想的名词，不一定准确）即可，如a=1，b=2，sum=3，sum-a按理来说是b，不赋值给b赋值给a就是自己说的错位赋值。

动画示意图如下：

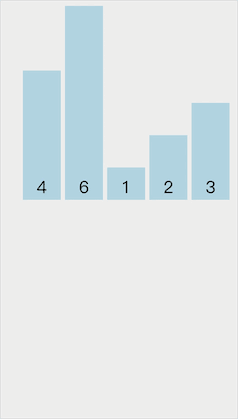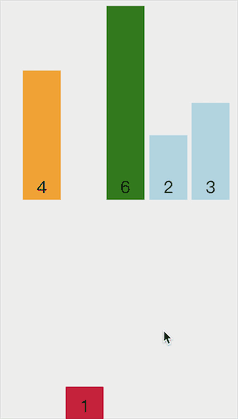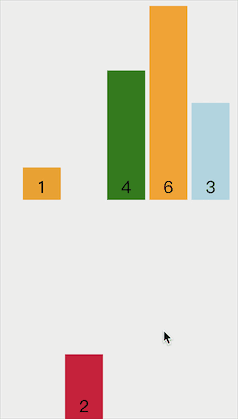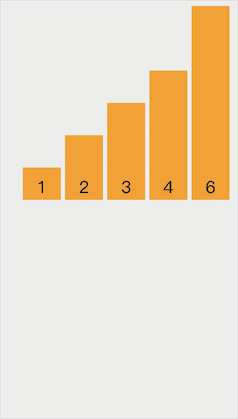
代码实现如下：

 1 import java.util.Scanner;
 2 
 3 public class InsertSort {
 4 
 5     public static void main(String[] args) {
 6         /**
 7          * 插入排序
 8          * 下面例子插入排序，就在原来数组的基础上进行，先从下标1的开始，因此下标为0的直接不用排，放到新数组的第一位即可
 9          * 如 4 6 1 2 3 升排序
10          * 1 先取出第一位放到新数组第一位，变成4
11          * 2 再取出第二位6，跟4进行比较，变成4 6
12          * 3 再取出第三位1，跟6比较，发现比它小，交换位置，变成4 1 6，然后1再与4比较，比4小再交换位置，变成1 4 6
13          * 4 再取出第四位2，与前面类似，它会逐渐跟6 4 比较，变成 1 2 4 6 ，然后2比1大不再变换位置
14          * 5 再取出最后一位3，与前面类似，他会逐一跟4 6进行比较，变成1 2 3 4 6
15          *
16          */
17 
18         //获取数组
19         Scanner scan = new Scanner(System.in);
20         System.out.println("输入数组长度");
21         int n = scan.nextInt();
22         int[] data = new int[n];
23         System.out.println("开始输入数组具体内容");
24         for (int i = 0; i < n; i++) {
25             data[i] = scan.nextInt();
26         }
27 
28         //排序前
29         System.out.println("排序前");
30         for (int i = 0; i < data.length; i++) {
31             System.out.print(data[i] + " ");
32         }
33         System.out.println();
34 
35         //插入排序，其实下面初略看好像不是插入排序，其实是比较浓缩的写法感觉是
36         for (int i = 1; i < n; i++) {//从索引1的位置开始逐一取出数准备进行插入比较
37             for (int j = i; j > 0; j--) {//拿出的这个数，逐一和它前面的数字进行比较
38                 if (data[j] < data[j - 1]) {
39                     //交换位置，使用另一种交换方法
40                     data[j] = data[j] + data[j - 1];
41                     data[j - 1] = data[j] - data[j - 1];
42                     data[j] = data[j] - data[j - 1];
43                 } else {
44                     //不用交换直接跳出内层循环，后面的不需要比了
45                     break;
46                 }
47             }
48         }
49         System.out.println("插入排序后");
50         //重新打印
51         for (int i = 0; i < data.length; i++) {
52             System.out.print(data[i] + " ");
53         }
54 
55     }
56 }

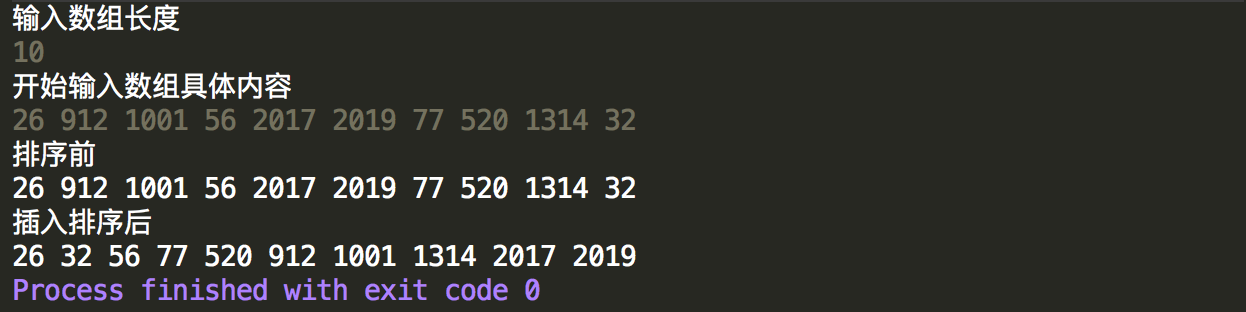
控制台输出结果，可以看出能正常的进行升序排列。直接插入排序的时间复杂度虽然也为O(n^2)，但是与冒泡排序有一点区别，冒泡是两两都要比较，因此其比较的次数必然为(n-1)+(n-2)+...+1=n(n-1)/2，而插入排序有点不同，虽然每次插入也要两两进行比较，但是比较到正确的插入位置就不再继续比较，因为以前的序列都是排好序的，因此它最坏的情况才是比较n(n-1)/2次。

参考《算法》，插入排序需要的交换次数和数组序列中倒置的对数相等，所谓倒置指的是数组中两个顺序颠倒的元素。另外比较的次数大于等于倒置的数量，小于等于倒置的数量加上（数组长度-1），倒置的必须要交换，因此也需要比较，所以比较次数大于等于倒置的数量很好理解，另外当插入的数理论上不是最左边的那个，这样除了要完成倒置所需要的比较外，还需要和左边的元素进行一次额外比较，确定插入的数是否到达了序列最左边的位置，其中除了第一个数外每一个数都需要一次额外的比较，因此比较次数小于等于倒置的数量加上（数组长度-1）。

希尔排序

学完了插入排序后，可以考虑一个极端的例子，如果数组序列中最小的数在最右边，而且序列要按照升序排序的话，那这个最小数如果插入要逐渐一步步的交换到最前面，并且每一步都需要交换，这样如果考虑性能肯定不是最优的，希尔排序就是出于提高插入排序的性能而出现的，其可以实现数据的大跨越交换，减少无意义的交换。

希尔排序中引入了步长的概念，插入排序是相邻元素一个一个的进行对比，希尔排序是按照步长间隔对元素进行对比。其过程是先初步对按照步长h分组的数据进行排序，最后再组合起来最后进行一次插入排序，单独分组排序再组合起来虽然看上去整体还是无序，但是实际上它的局部已经是有序状态，即任意间隔为h的元素都是有序的，当h为1时，就是完全有序状态。在排序的过程中，步长会逐渐递归直到变成1，即h=h/约数来递归缩小步长，这个约数一般常用就是2，当选择2时就是希尔增量。

import java.util.Scanner;

public class ShellSort {

    public static void main(String[] args) {
        /**
         * 希尔排序，是在插入排序的基础上进行了优化，引入了步长的概念，以前是一个一个的插入比较，现在是按照步长来先一一比较，
         * 意味着比较的两个元素不一定相邻，有可能索引相隔好几个数字，希尔排序每排完一次，步长会更新为新的步长，然后按照新的步长，
         * 继续比较排序，最后步长变成1，完成一次完整的插入排序，这样整个希尔排序完成。
         */

        //获取数组
        Scanner scan = new Scanner(System.in);
        System.out.println("输入数组的长度");
        int n = scan.nextInt();
        int[] data = new int[n];
        System.out.println("开始输入数组的具体内容");
        for (int i = 0; i < n; i++) {
            data[i] = scan.nextInt();
        }

        //排序前
        System.out.println("希尔排序前");
        for (int i = 0; i < data.length; i++) {
            System.out.print(data[i] + " ");
        }
        System.out.println();

        //希尔排序，引入了步长的概念
        int step = n;
        while (step >= 1) {
            step = step / 2;
            for (int i = step; i < n; i++) {//刚开始比较以数组长度/2作为步长，从步长的索引位置开始，往后开始比较
                for (int j = i; j - step >=0; j -= step) {
                    if (data[j] < data[j - step]) {
                        //交换位置，使用另一种交换方法
                        data[j] = data[j] + data[j - step];
                        data[j - step] = data[j] - data[j - step];
                        data[j] = data[j] - data[j - step];
                    } else {
                        //不用交换直接跳出内层循环，后面的不需要比了
                        break;
                    }
                }
            }
        }

        System.out.println("希尔排序后");
        //重新打印
        for (int i = 0; i < data.length; i++) {
            System.out.print(data[i] + " ");
        }

    }
}

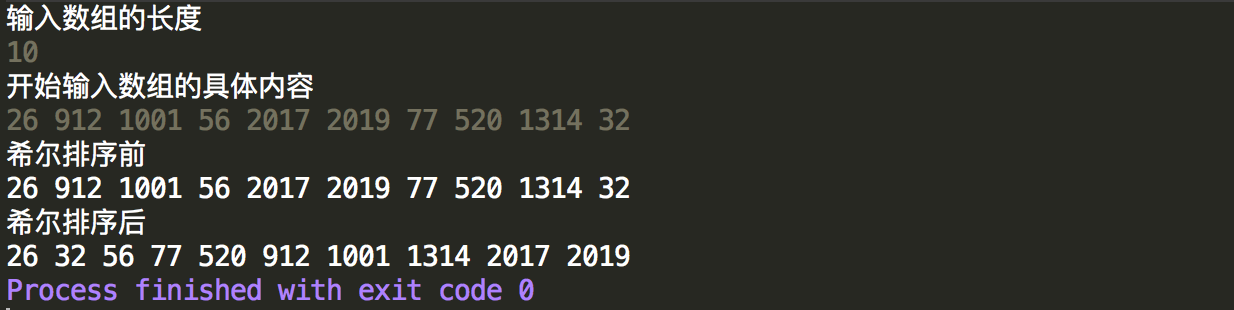
控制台输出结果，可以看出能正常的进行升序排列，希尔排序在希尔增量为2的情况下时间复杂度为O(n^2)。到目前为止依然不能确定哪种希尔增量就一定最好，这上升为一个数学问题了，暂时不深究。

快速排序

快速排序引入了基准数的概念，即比较的过程中数组元素都和基准数进行比较，一般基准数最理想就是取中值，比较完后比基准数小的在左边，比基准数大的在右边，这样完成一次快速排序并且确定一个元素的位置，然后再针对基准数左边的序列和右边的序列再次执行相同的快速排序，如此反复最后完成整个排序过程。

快速排序动画示意图（本想用上面同类型动画，但是发现实际算法跟这里的代码有点不一样就拷贝一个流行的动画图）：

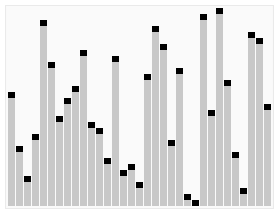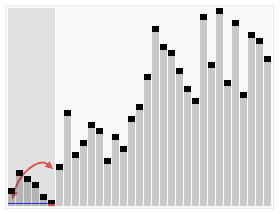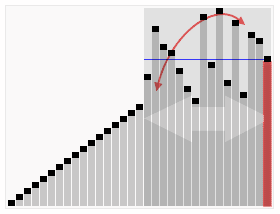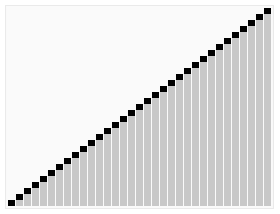
代码和例子分析如下，这是快速排序中的一种写法：

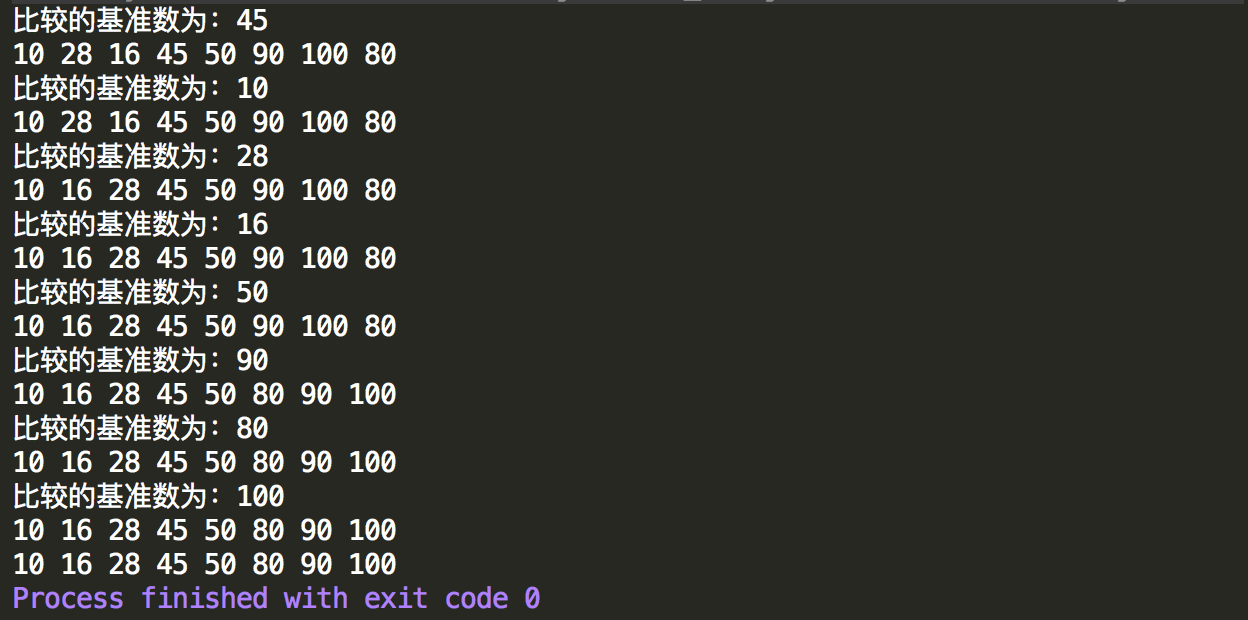
 1 public class QuickSort {
 2     /**
 3      * 快速排序，引入了基准数的概念，即根据基准数分成了2组，一组比基准数小，一组比基准数大。
 4      * 然后再次对两个分组使用快速排序，最后完成排序过程。
 5      * 排序需要遵守的规则：
 6      * （1）从右边开始，逐一和基准数进行比较，如果找到比基准数小的就进行更换
 7      * （2）从左边开始，逐一和基准数进行比较，如果找到比基准树大的就进行更换
 8      * 举例数组 45 28 80 90 50 16 100 10
 9      * 第一次排序 基准数为45
10      * 规则1执行后：10 28 80 90 50 16 100 45
11      * 规则2执行后：10 28 45 90 50 16 100 80
12      * 第二次排序，基准数还是45
13      * 规则1执行后：10 28 16 90 50 45 100 80
14      * 规则2执行后：10 28 16 45 50 90 100 80
15      * 第三次排序，基准数还是45
16      * 规则1执行后：没变，基准数右边找不到比它更小的
17      * 规则2执行后：没变，基准数左边找不到比它更大的
18      * 结束第一次快速排序，数组变成{10 28 16} 45 {50 90 100 80}
19      * 然后开始对左边和右边进行快速排序，继续执行上面的逻辑判断，很显然快速排序用到了递归的思想，因此需要写一个通用的排序方法可以反复调用
20      */
21 
22     public static void main(String[] args) {
23         int[] data=new int[]{45,28,80,90,50,16,100,10};
24         //快速排序
25         quickSort(data,0,data.length-1);
26         for (int i = 0; i < data.length; i++) {
27             System.out.print(data[i]+" ");
28         }
29     }
30 
31     /**
32      * 快速排序通用方法，参考子龙老师的代码学习
33      * @param data 需要进行快排的数组
34      * @param left 排序的范围：左边起始位置
35      * @param right 排序的范围：右边的起始位置
36      */
37     public static void quickSort(int[] data,int left,int right){
38         //在排序的过程中左边起始位置和右边起始位置会更新，因此需要定义变量先初始化
39         int ll=left;
40         int rr=right;
41         int base=data[left];//比较的基准数这里选择第一个数字
42 
43         //在比较的过程中，ll和rr会更新，最后当ll==rr时会停止比较
44         while(ll<rr){
45             //从右边开始跟基准数相比，如果比它小就进行数值更换
46             while(ll<rr&&data[rr]>=base){
47                 rr--;//如果从右边开始没找到比基准数小的，查找范围继续往数组左边移动
48             }
49             //最后有两种情况，一种是找到了，一种是没找到，如果是没找到，则最终ll==rr，找到了就是ll<rr
50             if(ll<rr){
51                 //将ll和rr位置对应的数字进行更换，其中data[ll]是基准数，替换完后data[rr]就是基准数
52                 int temp=data[ll];
53                 data[ll]=data[rr];
54                 data[rr]=temp;
55                 //左侧已经替换完一个小的数，从被替换位置开始往后移动一位，因为下次从左侧寻找比基准数大的数，这个数已经是小的所以不需要再找
56                 ll++;
57             }
58             //接着马上从左边开始跟基准数进行比较，如果比基准数大就进行更换
59             while(ll<rr&&data[ll]<=base){
60                 ll++;
61             }
62             if(ll<rr){
63                 //同上，进行更换，此时data[rr]就是基准数，与它进行更换，更换完成后data[ll]又变回了基准数，下一个循环依然是这个基准数
64                 int temp=data[ll];
65                 data[ll]=data[rr];
66                 data[rr]=temp;
67                 //跟上面类似，右侧rr索引处替换完一个比基准数大的数，下次从右侧找比基准数小的数就不需要从这个位置找了，直接左边移动一位开始找
68                 rr--;
69             }
70 
71         }
72 
73         System.out.println("比较的基准数为："+base);
74         printArray(data);
75 
76         //上面循环完成后完成第一次快速排序，接下来对基准数左边和右边继续进行快速排序
77         //左边快速排序
78         if(left<ll){
79             quickSort(data,left,ll-1);
80         }
81         //右边快速排序
82         if(right>rr){
83             quickSort(data,ll+1,right);
84         }
85 
86     }
87 
88     /**
89      * 为了方法，写一个输出数组的方法
90      * @param data
91      */
92     public static void printArray(int[] data){
93         for (int i = 0; i < data.length; i++) {
94             System.out.print(data[i]+" ");
95         }
96         System.out.println();
97     }
98 }

控制台输出结果，可以看出能正常的进行升序排列，快速排序的时间复杂度糟糕情况下为O(n^2)，一般情况为O(nlgn)。所谓的糟糕情况是数组完全有序，算法就退化成了冒泡排序，如数组本来是从小到大排列的，这样根据代码基准数都是取得左边第一个数，导致从右边找比它小的需要整个遍历才能确定其位置，然后将第一个数划去，右边剩余的数组序列继续使用快速排序，发现还是需要再循环遍历一遍数组，因此比较的次数跟冒泡排序一样，这是最极端的情况。

另外参考网上博客，修改了上面快速排序的代码，也可以实现排序，对于快速排序还需要以后多多理解，个人感觉自己还没有完全懂。

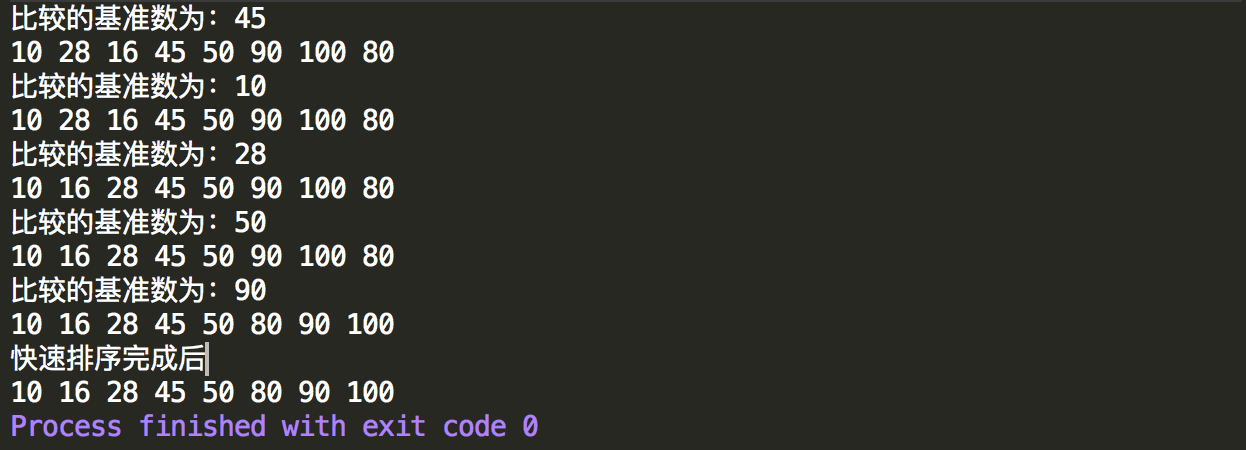
 1 public class QuickSortNew {
 2     /**
 3      *快速排序重写，换另外一种写法
 4      */
 5 
 6     public static void main(String[] args) {
 7         int[] data=new int[]{45,28,80,90,50,16,100,10};
 8         //测试快速排序
 9         quickSort(data,0,data.length-1);
10 
11         System.out.println("快速排序完成后");
12 
13         for (int i = 0; i < data.length; i++) {
14             System.out.print(data[i]+" ");
15         }
16     }
17 
18     /**
19      * 快速排序具体实现，配合递归
20      */
21     public static void quickSort(int[] data,int left,int right){
22         if(left<right){
23             int pivot=partion(data,left,right);
24             //对基准值左边的数组继续进行划分
25             quickSort(data,left,pivot-1);
26             //对基准值左边的数组继续进行划分
27             quickSort(data,pivot+1,right);
28         }
29     }
30 
31     /**
32      * 参考博客，先对数组进行划分，变成两部分，并返回基准数的位置
33      * @param data 需要进行快排的数组
34      * @param left 排序的范围：左边起始位置
35      * @param right 排序的范围：右边的起始位置
36      */
37     public static int partion(int[] data,int left,int right){
38         //在排序的过程中左边起始位置和右边起始位置会更新，因此需要定义变量先初始化
39         int ll=left;
40         int rr=right;
41         int base=data[left];//比较的基准数为第一个数字
42 
43         //在比较的过程中，ll和rr会更新，最后当ll==rr时会停止比较
44         while(ll<rr){
45             //从右边开始跟基准数相比，如果比它小就进行数值更换
46             while(ll<rr&&data[rr]>=base){
47                 rr--;//如果从右边开始没找到比基准数小的，查找范围继续往数组左边移动
48             }
49             //最后有两种情况，一种是找到了，一种是没找到，如果是没找到，则最终ll==rr，找到了就是ll<rr
50             if(ll<rr){
51                 //将ll和rr位置对应的数字进行更换，其中data[ll]是基准数，替换完后data[rr]就是基准数
52                 int temp=data[ll];
53                 data[ll]=data[rr];
54                 data[rr]=temp;
55                 //左侧已经替换完一个小的数，从被替换位置开始往后移动一位，因为下次从左侧寻找比基准数大的数，这个数已经是小的所以不需要再找
56                 ll++;
57             }
58             //接着马上从左边开始跟基准数进行比较，如果比基准数大就进行更换
59             while(ll<rr&&data[ll]<=base){
60                 ll++;
61             }
62             if(ll<rr){
63                 //同上，进行更换，此时data[rr]就是基准数，与它进行更换，更换完成后data[ll]又变成了基准数
64                 int temp=data[ll];
65                 data[ll]=data[rr];
66                 data[rr]=temp;
67                 //跟上面类似，右侧替换完一个比基准数大的数，下次从右侧找比基准数小的数就不需要从这个位置找了，直接左边移动一位开始找
68                 rr--;
69             }
70         }
71 
72         System.out.println("比较的基准数为："+base);
73         printArray(data);
74 
75         //比较完一次后，可以确定新的基准值的位置
76         return ll;
77     }
78 
79     /**
80      * 为了方法，写一个输出数组的方法
81      * @param data
82      */
83     public static void printArray(int[] data){
84         for (int i = 0; i < data.length; i++) {
85             System.out.print(data[i]+" ");
86         }
87         System.out.println();
88     }
89 
90 }