Java集合-数据结构之栈、队列、数组、链表和红黑树
数据结构部分,复习栈,队列,数组,链表和红黑树,参考博客和资料学习后记录到这里方便以后查看,感谢被引用的博主。
栈
栈(stack)又称为堆栈,是线性表,它只能从栈顶进入和取出元素,有先进后出,后进先出(LIFO, last in first out)的原则,并且不允许在除了栈顶以外任何位置进行添加、查找和删除等操作。栈就相当如手枪的弹夹,先进入栈的数据被压入栈底(bottom),而后入栈的数据存放在栈顶(top)。当需要出栈时,是先让栈顶的数据出去后,下面的数据才能出去,这就是先进后出的特点。插入数据一般称为进栈或压栈(push),删除数据则称为出栈或弹栈(pop)。
下面参考博文,地址:https://www.cnblogs.com/ysocean/p/7911910.html,底层使用数组来模拟一个栈的功能,具有push,pop,peek等常用方法,原生的stack是继承自vector类的子类,其具备父类的所有方法,这里模拟除了前面三种方法外,还写了判断自定义栈是否为空,以判断自定义栈是否满等方法。
自定义栈,底层采用数组模拟
1 package dataStructure; 2 /** 3 * 自定义栈,使用数组来实现 4 */ 5 public class MyStack { 6 7 private int size;//数组大小 8 private String[] arr;//数组 9 private int top=-1;//默认栈顶位置 10 11 //构造方法 12 public MyStack(int size) { 13 this.size = size; 14 arr=new String[size]; 15 } 16 17 //压栈 18 public void push(String value){ 19 //top范围0到size-1 20 if(top<=size-2){ 21 arr[++top]=value; 22 } 23 } 24 25 //出栈 26 public String pop(){ 27 //原栈顶元素设置为null,等待gc自动回收 28 return arr[top--]; 29 } 30 31 //查看栈顶 32 public String peek(){ 33 if(top>-1){ 34 return arr[top]; 35 }else{ 36 return null; 37 } 38 } 39 40 //检查栈是否为空 41 public boolean Empty(){ 42 return top<0; 43 } 44 45 //检查栈是否满 46 public boolean Full(){ 47 return top==size-1; 48 } 49 50 //检查栈中元素数量 51 public String size(){ 52 int count=top+1; 53 return "栈中元素:"+count+" | 栈容量"+size; 54 } 55 56 }
测试代码,验证自定义栈中的方法。
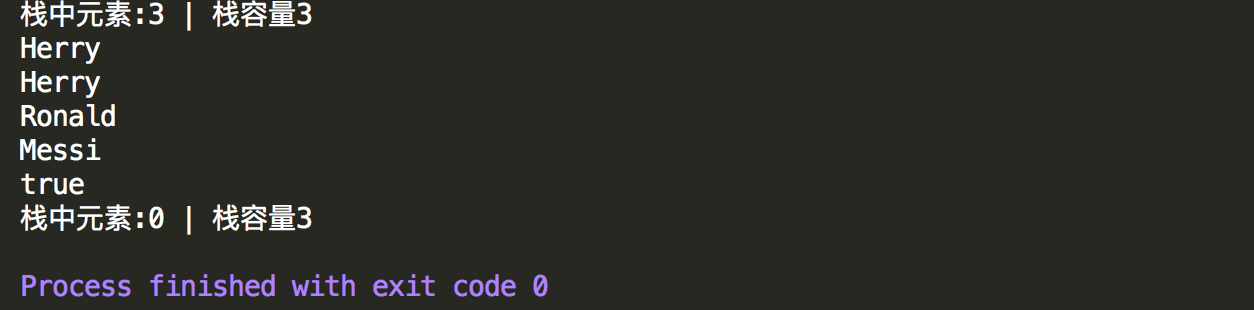
1 package dataStructure; 2 3 public class TestMyStack { 4 5 public static void main(String[] args) { 6 //测试自定义Stack 7 MyStack stack=new MyStack(3); 8 //压入栈顶 9 stack.push("Messi"); 10 stack.push("Ronald"); 11 stack.push("Herry"); 12 13 //查看栈中元素数量 14 System.out.println(stack.size()); 15 16 //查看栈顶元素 17 System.out.println(stack.peek()); 18 19 //循环遍历栈中元素 20 while(!stack.Empty()){ 21 System.out.println(stack.pop()); 22 } 23 24 //判断栈是否为空 25 System.out.println(stack.Empty()); //true 26 System.out.println(stack.size()); 27 28 } 29 30 }
控制台输出情况。
自定义一个栈,实现数组自动扩容并能储存不同的数据类型
在上面例子的基础上,依然参考上述博文,自定义一个栈并能实现栈容量自动扩容,以及栈中可以存储不同的数据类型。
1 package dataStructure; 2 3 import java.util.Arrays; 4 import java.util.EmptyStackException; 5 6 /** 7 * 自定义栈,使用数组来实现,可以实现数组自动扩容,以及存储不同的数据类型 8 */ 9 public class MyArrayStack { 10 //定义属性 11 private int size;//容量 12 private Object[] arr;//对象数组 13 private int top;//栈顶位置 14 15 //默认构造方法 16 public MyArrayStack() { 17 this.size=10; 18 this.arr=new Object[10]; 19 this.top=-1; 20 } 21 22 //自定义数组容量的构造方法 23 public MyArrayStack(int size) { 24 if(size<0){ 25 throw new IllegalArgumentException("栈容量不能小于0"+size); 26 } 27 this.size = size; 28 this.arr=new Object[size]; 29 this.top=-1; 30 } 31 32 //压栈 33 public Object push(Object value){ 34 //压栈之前欠判断数组容量是否足够,不够就扩容 35 getNewCapacity(top+1); 36 arr[++top]=value; 37 return value; 38 } 39 40 //出栈 41 public Object pop(){ 42 if(top==-1){ 43 throw new EmptyStackException(); 44 } 45 Object obj=arr[top]; 46 //删除原来栈顶的位置,默认设置为null,等待gc自动回收 47 arr[top--]=null; 48 return obj; 49 } 50 51 //查找栈顶的元素 52 public Object peek(){ 53 return arr[top]; 54 } 55 56 //判断栈是否为空 57 public boolean Empty(){ 58 return top==-1; 59 } 60 61 //检查栈中元素 62 public String size(){ 63 int count=top+1; 64 return "栈中元素:"+count+" | 栈容量"+size; 65 } 66 67 //返回栈顶到数组末端内容 68 public void printWaitPosition(){ 69 if(top<arr.length-1){ 70 for(int i=top+1;i<arr.length;i++){ 71 System.out.println("空闲位置数值为:"+arr[i]); 72 } 73 }else{ 74 System.out.println("没有空闲位置"); 75 } 76 } 77 78 79 //写一个方法判断数组是否需要自动扩容 80 public boolean getNewCapacity(int index){ 81 //判断压入后的数组下标,是否超过了数组容量限制,超出就扩容 82 if(index>size-1){ 83 //扩容2倍 84 int newSize=0; 85 if((size<<1)-Integer.MAX_VALUE>0){ 86 newSize=Integer.MAX_VALUE; 87 }else{ 88 newSize=size<<1; 89 } 90 //数组扩容后复制原数组数据,扩容的部分,默认为Object初始值 91 this.size=newSize; 92 arr=Arrays.copyOf(arr, newSize); 93 return true; 94 }else{ 95 return false; 96 } 97 } 98 }
测试代码,验证自动扩容,空闲位置是什么。
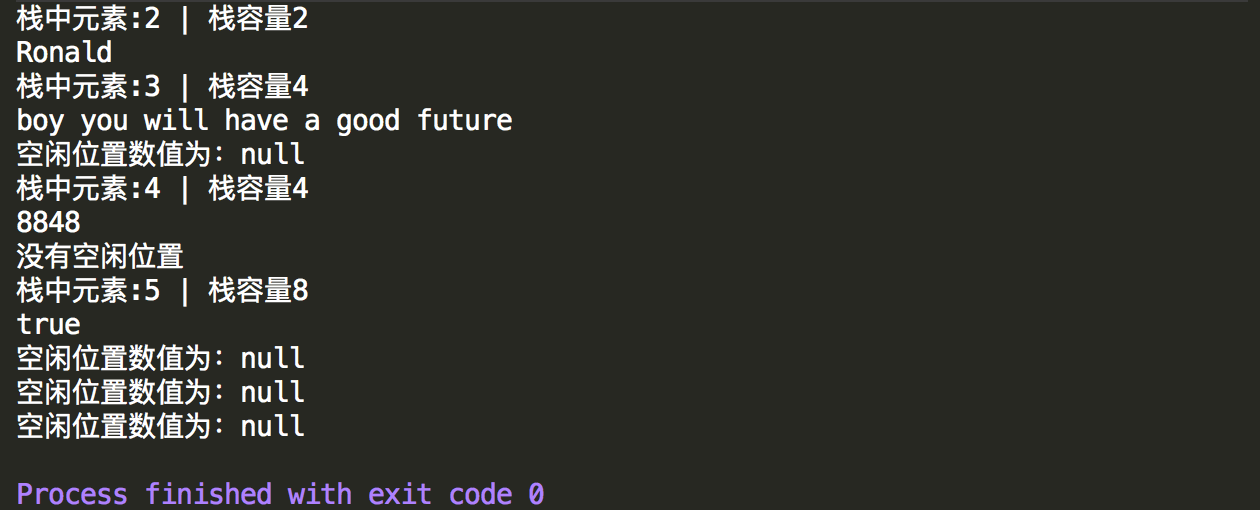
1 package dataStructure; 2 3 public class TestMyArrayStack { 4 5 public static void main(String[] args) { 6 // 测试自定义MyArrayStack 7 MyArrayStack stack=new MyArrayStack(2); 8 stack.push("Messi"); 9 stack.push("Ronald"); 10 System.out.println(stack.size()); 11 System.out.println(stack.peek()); 12 //超出容量后继续压栈 13 stack.push("boy you will have a good future"); 14 System.out.println(stack.size()); 15 System.out.println(stack.peek()); 16 //打印stack中空闲位置内容 17 stack.printWaitPosition(); 18 //压入数字 19 stack.push(8848); 20 System.out.println(stack.size()); 21 System.out.println(stack.peek()); 22 stack.printWaitPosition(); 23 //压入布尔类型 24 stack.push(true); 25 System.out.println(stack.size()); 26 System.out.println(stack.peek()); 27 stack.printWaitPosition(); 28 } 29 }
控制台输出情况。
在参考博文中,栈除了以上用途外,还可以巧妙用在将字符串反转,还有验证分隔符是否匹配,以后如果有需要可以参考引用的博文。
队列
队列(queue),跟堆栈类似,也是线性表,它是仅允许在尾部(tail)进行插入,在头部(head)进行删除,满足先进先出(FIFO)的原则,类似火车头进入山洞,先进入山洞的车厢就先出来山洞,后进入山洞的火车头后出来山洞。查看队列源码,可以看到接口有如下方法。
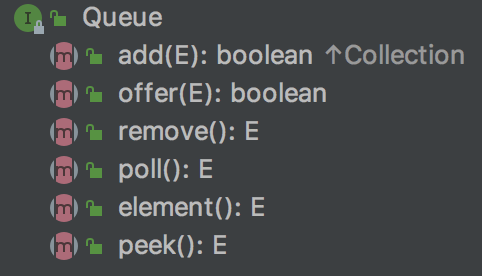
简单的整理一下如下。
(1)插入元素到tail尾部:add(e),offer(e),前者为执行失败时抛出异常,后者不会抛出但返回特殊值(null或false)。
(2)移除head头部元素:remove(),poll(),前者为执行失败时抛出异常,后者不会抛出但返回特殊值(null或false)。
(3)查看列头head元素:element(),peek(),前者为执行失败时抛出异常,后者不会抛出但返回特殊值(null或false)。
下面分别使用两种类型的方法进行queue操作。
使用会抛出异常的方法
1 package DataCompose; 2 3 import java.util.LinkedList; 4 import java.util.PriorityQueue; 5 import java.util.Queue; 6 7 /** 8 * 测试队列,队列Queue具有先进先出的特点 9 */ 10 public class QueueTest { 11 12 public static void main(String[] args) { 13 //创建一个队列,使用LinkedList来创建对象,并被接口指向 14 Queue<String> queue=new LinkedList<String>(); 15 //Queue<String> queue=new PriorityQueue<String>(); 16 //使用会抛出异常的方法,添加元素到尾部,删除头部元素,以及查看头部元素操作 17 18 //1 添加元素 add方法 19 queue.add("Messi"); 20 queue.add("Herry"); 21 queue.add(null); 22 System.out.println(queue); 23 24 //2 删除头部元素 remove方法 25 String str=queue.remove(); 26 System.out.println(str); 27 System.out.println(queue); 28 29 //3 查看头部元素 element方法 30 System.out.println(queue.element()); 31 32 } 33 }
控制台输出结果,可以看出如果实现类为LinkedList时可以插入null,并且看出先加入的Messi,如果执行remove方法后也是先移除,执行element方法也是先查询得到头部元素,因此遵循先进先出原则。
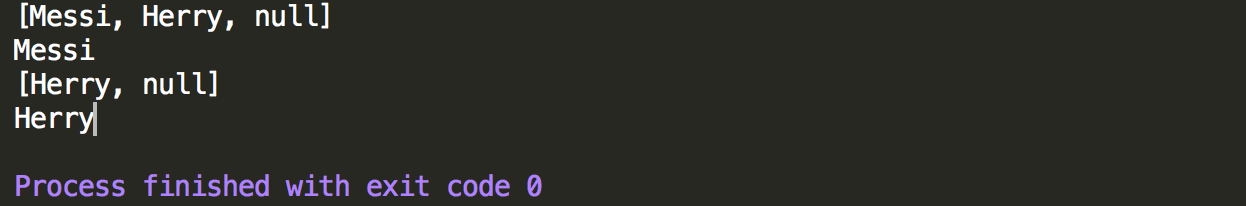
如果不往集合中add元素,直接执行remove方法会发生如下报错,提示没有元素异常,并发现执行remove方法,会执行LinkedList底层的removeFirst方法,说明其移除的就是第一个元素。

同样如果不往集合中添加元素,直接执行element方法会报如下错,也提示没有元素异常,并发现执行element方法时会调用底层的getFirst方法,说明它取得是第一个元素。

可以看出当队列的实现类为LinkedList时,是可以插入null的,如果把实现类更换为PriorityQueue,会发生什么呢?发现会报空指针异常,原因是优先队列不允许插入null。

以上是使用queue的add,remove和element方法,上述同样的情况下,如果更换成offer,poll和peek方法后会是什么情况,看如下代码测试。
1 package DataCompose; 2 3 import java.util.LinkedList; 4 import java.util.PriorityQueue; 5 import java.util.Queue; 6 7 /** 8 * 测试队列,队列Queue具有先进先出的特点 9 */ 10 public class QueueTest1 { 11 12 public static void main(String[] args) { 13 //创建一个队列,使用LinkedList来创建对象,并被接口指向 14 Queue<String> queue=new LinkedList<String>(); 15 //Queue<String> queue=new PriorityQueue<String>(); 16 //使用会抛出异常的方法,添加元素到尾部,删除头部元素,以及查看头部元素操作 17 18 //1 添加元素 offer方法 19 queue.offer("Messi"); 20 queue.offer("Herry"); 21 queue.offer(null); 22 System.out.println(queue); 23 24 //2 删除头部元素 poll方法 25 String str=queue.poll(); 26 System.out.println(str); 27 System.out.println(queue); 28 29 //3 查看头部元素 peek方法 30 System.out.println(queue.peek()); 31 32 } 33 }
以上代码正常情况下执行跟第一种情况一模一样的结果,如果集合为空,直接调用poll方法和peek方法,查看执行结果如下,发现输出均为null,说明在集合为空的情况下这两种方法不会抛出异常。

同样如果将实现类更换为PriorityQueue,往里面添加null,会是什么结果呢?发现依然抛出异常,主要原因查看offer源码发现,如果实现类不支持null就会抛出异常。

另外还有一个deque,是queue的子接口,为双向队列,可以有效的在头部和尾部同时添加或删除元素,其实现类为ArrayDeque和LinkedList类,如果需要一个循环数组队列,选择ArrayDeque,如果需要一个链表队列,使用实现了Queue接口的LinkedList类。
由于Deque实现了Queue接口,因此其可以表现为完全的Queue特征,同时也可以当做栈来使用,具体是Queue还是栈,根据执行的方法来选择,一般来说如果添加元素和删除元素都是在同一端执行(方法后面都为First),就表现为栈的特性,否则就是Queue的特性,以下是Deque接口的方法。
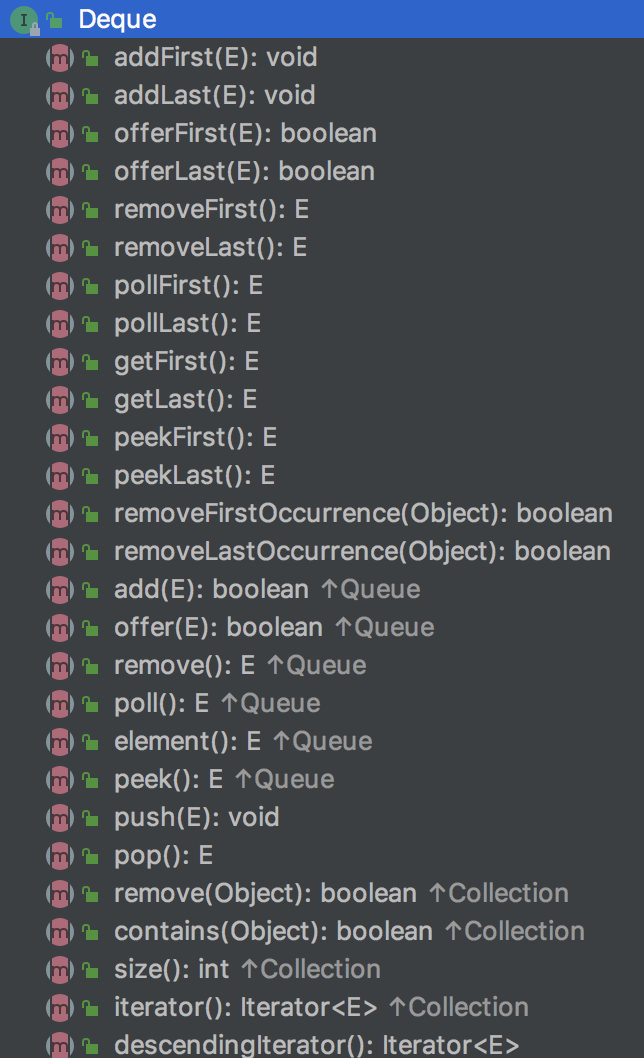
从以上的方法列表中,大概可以总结出以下几个特点:
(1)凡是以add,remove和get开头的方法,都可能在执行的过程中抛出异常,而以offer,poll和peek的方法往往返回null或者其他。
(2)凡是方法后面有Queue接口标志的方法,说明其是继承自接口Queue的方法,有Collection标志的说明是继承自Collection接口的通用方法。
Deque方法参考博文,分类总结如下:
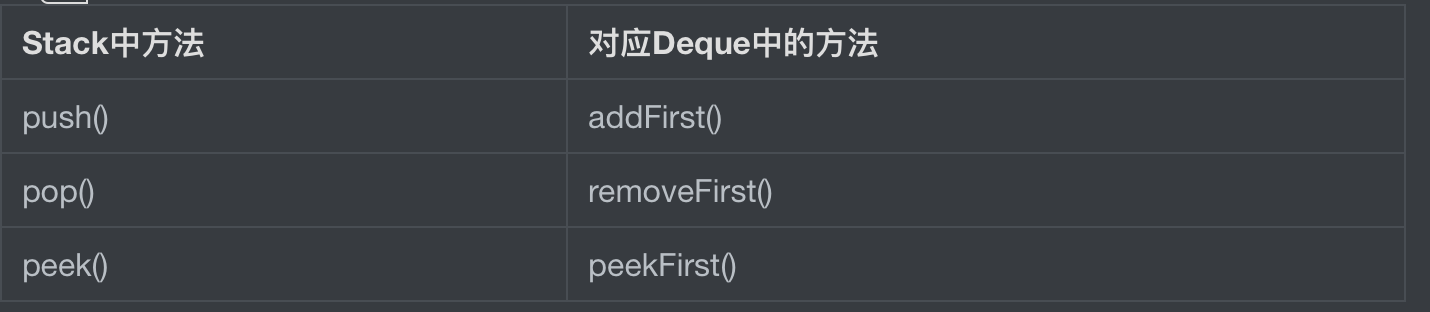
deque和栈的方法对照表
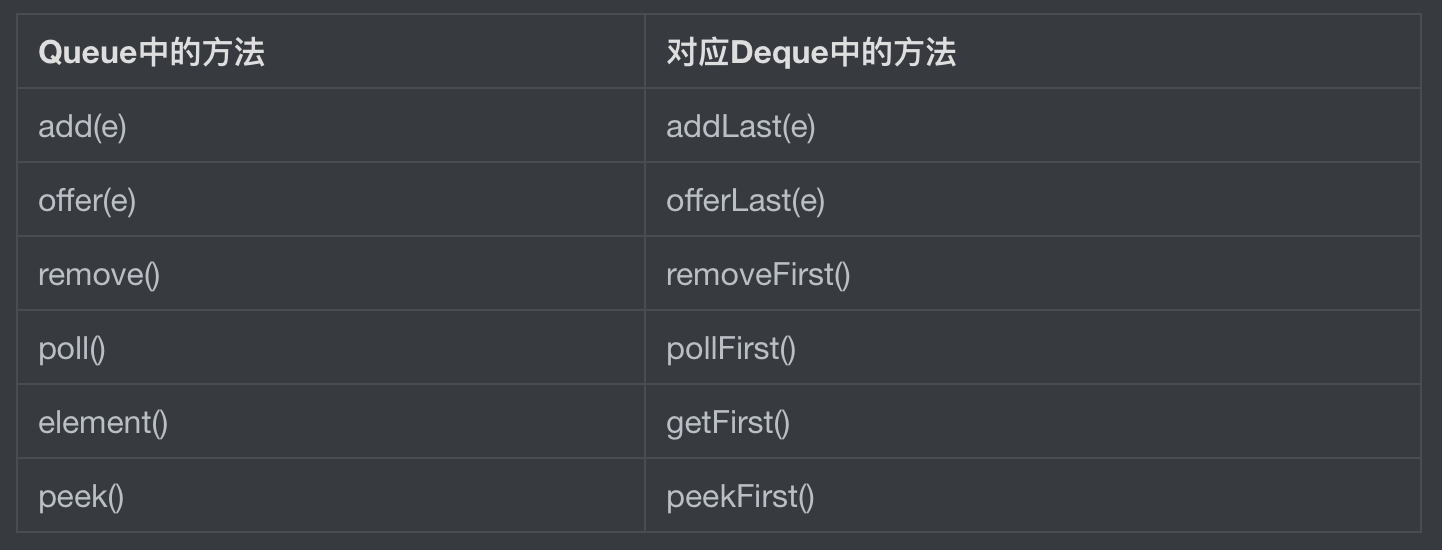
deque和queue的方法对照表
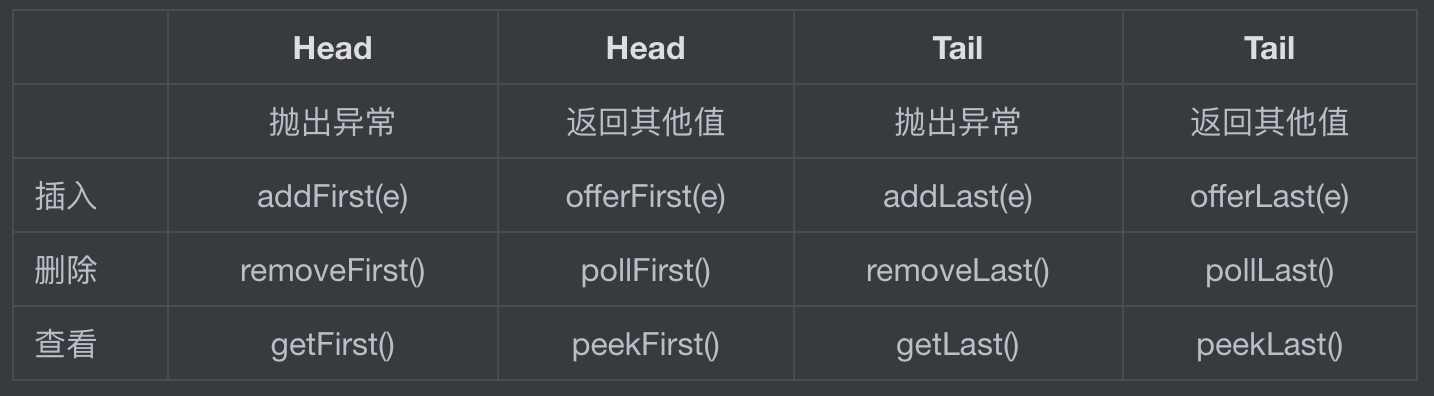
deque中抛出异常和返回其他值的方法
下面简单的用deque的方法来实现集合操作,从队列两端添加,删除和查看元素,和栈以及queue的相关方法不在这里测试了,未来工作中继续感受。
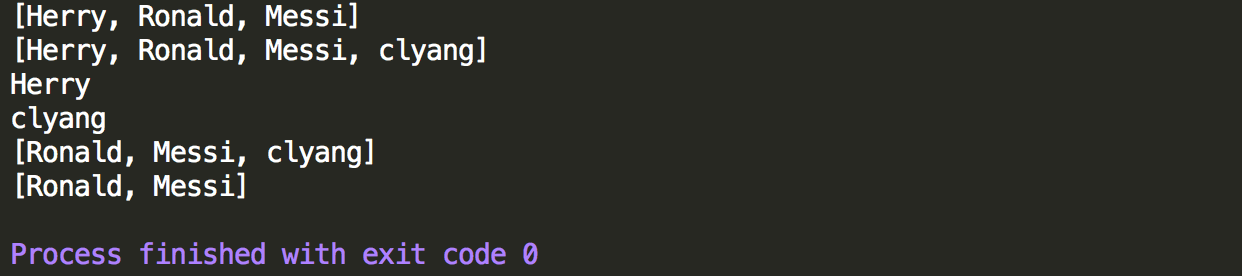
1 package DataCompose; 2 3 import java.util.Deque; 4 import java.util.LinkedList; 5 6 /** 7 * 测试双向队列,其可以表现为Queue,也可以表现为Stack,这里测试双向列队 8 */ 9 public class DequeTest { 10 11 public static void main(String[] args) { 12 //使用链表实现 13 Deque<String> deque=new LinkedList<>(); 14 15 //先在head插入元素 16 deque.offerFirst("Messi"); 17 deque.offerFirst("Ronald"); 18 deque.offerFirst("Herry"); 19 System.out.println(deque); 20 21 //在tail插入元素 22 deque.offerLast("clyang"); 23 System.out.println(deque); 24 25 //在head查看元素 26 System.out.println(deque.peekFirst()); 27 28 //在tail查看元素 29 System.out.println(deque.peekLast()); 30 31 //在head删除元素 32 deque.pollFirst(); 33 System.out.println(deque); 34 35 //在tail删除元素 36 deque.pollLast(); 37 System.out.println(deque); 38 39 } 40 }
控制台输出结果,可以看出deque可以在head和tail两端进行插入、删除和查看操作。
数组
数组(Array),是一种有序的元素序列,数组在内存中开辟一段连续的空间,并在连续的空间存放数据,查找数组可以通过数组索引来查找,因此查找速度快,但是增删元素慢。数组创建以后在程序运行期间长度是不变的,如果要增加一个元素,会创建一个新的数组,将新元素存储到索引位置,并将原数组根据索引一一复制到新数组,原来的数组被gc回收,新数组的内存地址赋值给数组变量。
关于数组部分,直接可以从自己写的博客查看具体内容,博客地址:https://www.cnblogs.com/youngchaolin/p/10987960.html,另外参考了大牛博客,进行一些知识面的扩展。
底层利用数组,也可以实现数据结构的基本功能,简单概括一下,就是需要具备增删改查循环遍历的功能,这样才能算实现基本的数据结构,下面参考博客,进行这些功能的封装,实现一个基于数组的简单数据结构。
1 package DataCompose; 2 3 /** 4 * 数组测试,理解最基本数据结构,利用数组封装一个简单的数据结构,实现增删改查和循环遍历 5 */ 6 public class ArrayTest { 7 //底层数组,使用Object类型 8 private Object[] arr; 9 //数组占用长度 10 private int length; 11 //数组容量 12 private int maxSize; 13 14 //默认构造方法,仿造ArrayList,默认长度为10 15 public ArrayTest() { 16 this.length=0; 17 this.maxSize=10; 18 arr=new Object[maxSize]; 19 } 20 21 //自定义数组长度 22 public ArrayTest(int maxSize) { 23 this.maxSize = maxSize; 24 this.length=0; 25 arr=new Object[maxSize]; 26 } 27 //增加元素 28 public boolean add(Object obj){ 29 //增加元素暂时不使用底层再创建一个新的数组,进行数组内容复制,参考博客直接添加 30 if(length==maxSize){ 31 System.out.println("数组容量达到极限,无法自动扩容"); 32 return false; 33 } 34 //原数组后面再添加一个元素,否则就是初始值null 35 arr[length++]=obj; 36 return true; 37 } 38 //查找元素,本来先要写删,但是删元素之前需要先查是否存在,因此先写查询方法 39 public int find(Object obj){ 40 int n=-1; 41 for (int i= 0; i< length; i++) { 42 if(obj.equals(arr[i])){ 43 n=i; 44 break; 45 } 46 } 47 return n; 48 } 49 //删除元素 50 public boolean remove(Object obj){ 51 52 if(obj==null){ 53 System.out.println("不能删除null,请输入正常内容"); 54 return false; 55 } 56 int index=find(obj); 57 if(index==-1){ 58 System.out.println("不存在的元素:"+obj); 59 return false; 60 } 61 //数组元素覆盖操作 62 if(index==length-1){ 63 length--; 64 }else{ 65 for(int i=index;i<length-1;i++){ 66 arr[i]=arr[i+1]; 67 } 68 length--; 69 } 70 return true; 71 } 72 //修改元素,直接修改数组索引上的元素 73 public boolean modify(int index,Object obj){ 74 if(index<0||index>length-1){ 75 System.out.println("数组下标越界"); 76 return false; 77 }else{ 78 arr[index]=obj; 79 return true; 80 } 81 } 82 //遍历输出内容 83 public void toArrayString() { 84 System.out.print("["); 85 for (int i = 0; i < length; i++) { 86 if(i<length-1){ 87 System.out.print(arr[i] + ","); 88 }else{ 89 System.out.print(arr[i]); 90 } 91 } 92 System.out.print("]"); 93 //换行 94 System.out.println(); 95 } 96 97 }
测试类来测试上面写的数据结构。
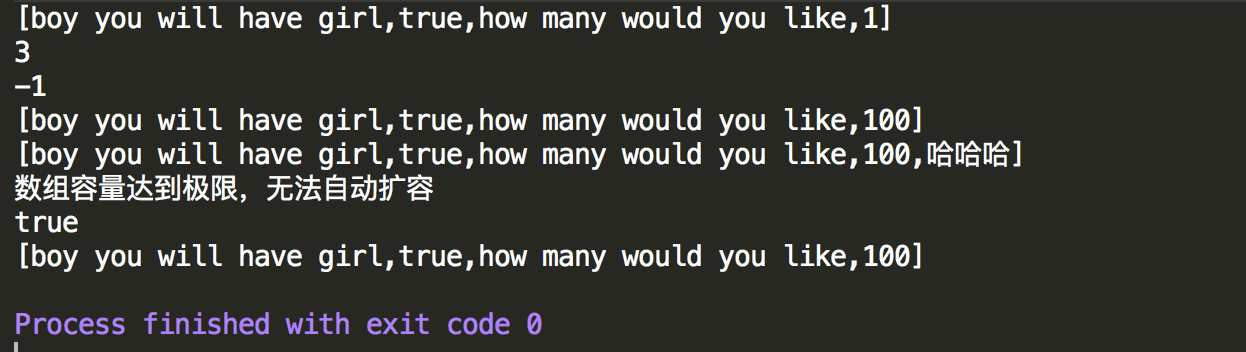
1 package DataCompose; 2 3 /** 4 * 测试自己底层用数组写的数据结构 5 */ 6 public class TestArrayTest { 7 8 public static void main(String[] args) { 9 ArrayTest arr=new ArrayTest(5); 10 //添加元素 11 arr.add("boy you will have girl"); 12 arr.add(true); 13 arr.add("how many would you like"); 14 arr.add(1); 15 16 //打印数组 17 arr.toArrayString(); 18 19 //查询为1的元素 20 System.out.println(arr.find(1)); 21 22 //查询'你好' 23 System.out.println(arr.find("你好")); 24 25 //修改下标为3的数组为100 26 arr.modify(3,100); 27 arr.toArrayString(); 28 29 //再添加一个元素 30 arr.add("哈哈哈"); 31 arr.toArrayString(); 32 33 //继续添加 34 arr.add("ok?"); 35 36 //删除最后的元素 37 boolean result=arr.remove("哈哈哈"); 38 System.out.println(result); 39 arr.toArrayString(); 40 41 } 42 }
控制台输出情况,发现可以正常的实现增删改查和循环遍历的功能。
链表
链表(linked list),是由一系列结点node组成,结点包含两个部分,一个是存储数据的数据域,一个是存储下一个节点地址以及自己地址的地址域,即链表是双向链接的(double linked),多个节点通过地址进行连接,组成了链表,其特点是增删元素快,只要创建或删除一个新的节点,内存地址重新指向规划就行,但是查询元素慢,需要通过连接的节点从头开始依次向后查找。
链表有单向链表和双向链表之分。
单向链表:链表中只有一条'链子',元素存储和取出的顺序可能不一样,不能保证元素的顺序。
双向链表:链表中除了有单向链表一条链子外,还有一条链子用于记录元素的顺序,因此它可以保证元素的顺序。
单向链表的实现
依然参考博主系列文章的链表,自己实现一个自定义的链表,并具有增加头部元素、删除指定元素、修改指定元素、查找元素以及展示链表内容等功能。
1 package DataCompose; 2 3 /** 4 * 单向列表测试, 5 */ 6 public class SingleLinkTest { 7 //定义链表大小 8 private int size; 9 //定义头节点,只需要定义一个头,其他元素都可以通过这个节点头来找到 10 private Node head; 11 12 public SingleLinkTest() { 13 this.size = 0; 14 this.head = null; 15 } 16 17 //在链表头部增加元素 18 public Object addHead(Object obj) { 19 //得到一个新的节点 20 Node newNode = new Node(obj); 21 //链表为空,将头元素数据设置为obj 22 if (size == 0) { 23 head = newNode; 24 } else { 25 newNode.next = head; 26 head = newNode; 27 } 28 this.size++; 29 return obj; 30 } 31 32 //在链表中删除元素 33 public boolean delete(Object obj) { 34 //要删除一个元素,需要首先找到这个元素,将这个元素前一个元素next属性指向这个元素的下一个元素 35 if (size == 0) { 36 System.out.println("链表为空,无法删除!"); 37 return false; 38 } 39 //都是从头部开始查询,有找到需要删除的节点就删除,删除后将这个节点前一个节点next属性指向删除节点的下一个节点 40 //需要重新指向的话,需要删除节点数据,也需要删除节点前一个节点的数据,刚开始都使用头部节点数据 41 Node previousNode = head; 42 Node currentNode = head; 43 //什么时候找到这个元素什么时候停止 44 while (!currentNode.data.equals(obj)) { 45 //节点往后遍历,寻找下一个节点数据 46 if (currentNode.next == null) { 47 System.out.println("已到链表末尾,无需要删除的元素"); 48 return false; 49 } else { 50 //重置当前结点和当前结点前一个结点 51 previousNode = currentNode; 52 currentNode = currentNode.next; 53 } 54 } 55 56 //能执行到这里说明有需要删除的元素 57 size--; 58 if (currentNode == head) { 59 head = currentNode.next; 60 } else { 61 previousNode.next = currentNode.next; 62 } 63 return true; 64 } 65 66 //修改元素 67 public boolean modify(Object old, Object newObj) { 68 if (size == 0) { 69 System.out.println("链表为空,无法修改元素"); 70 return false; 71 } 72 Node currentNode = head; 73 while (!currentNode.data.equals(old)) { 74 if (currentNode.next == null) { 75 System.out.println("已到链表末尾,无需要删除的元素"); 76 return false; 77 } else { 78 currentNode = currentNode.next; 79 } 80 } 81 82 //能执行到这里说明有相同的元素 83 currentNode.data = newObj; 84 return true; 85 86 } 87 88 //查找元素 89 public boolean find(Object obj) { 90 if (size == 0) { 91 System.out.println("链表为空"); 92 } 93 Node currentNode = head; 94 while (!currentNode.data.equals(obj)) { 95 if (currentNode.next == null) { 96 System.out.println("已到链表末尾,无查找的元素"); 97 return false; 98 } else { 99 currentNode = currentNode.next; 100 } 101 } 102 103 //能执行到这里说明查找到了元素 104 System.out.println("查找元素存在链表中"); 105 return true; 106 } 107 108 //遍历输出元素 109 public void toLinkString() { 110 if (size > 0) { 111 if (size == 1) { 112 System.out.println("[" + head.data + "]"); 113 } 114 //结点先从头部开始 115 Node currentNode = head; 116 for (int i = 0; i < size; i++) { 117 if (i == 0) { 118 System.out.print("[" + currentNode.data); 119 } else if (i < size - 1) { 120 System.out.print("--->" + currentNode.data); 121 } else{ 122 System.out.print("--->"+currentNode.data+"]"); 123 } 124 currentNode = currentNode.next; 125 } 126 } else { 127 System.out.println("[]"); 128 } 129 System.out.println(); 130 } 131 132 }
Node外部类,参考很多博客都是写成内部类,也可以写成外部类。

1 package DataCompose; 2 3 /** 4 * 节点,外部类实现,自定义链表用 5 */ 6 public class Node { 7 //数据部分 8 public Object data; 9 //指向下一个节点,没有修改其中值得情况下默认为null 10 public Node next; 11 12 public Node(Object data) { 13 this.data = data; 14 } 15 16 }
测试类代码。
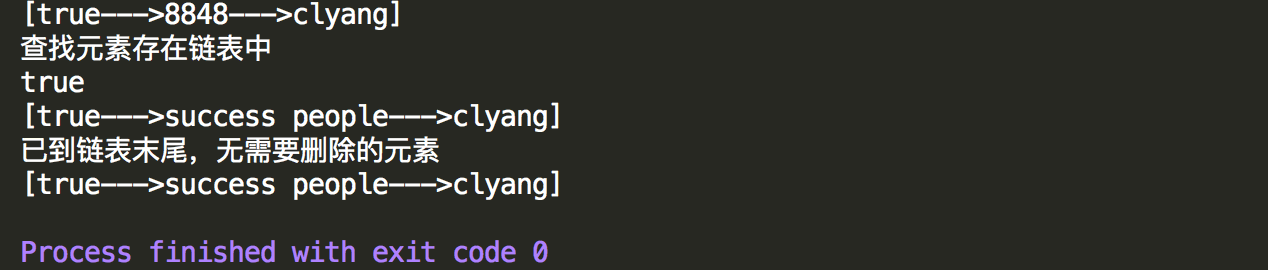
1 package DataCompose; 2 3 /** 4 * 测试自定义单向链表 5 */ 6 public class TestSingleLinkTest { 7 8 public static void main(String[] args) { 9 //默认容量为0的链表 10 SingleLinkTest Link=new SingleLinkTest(); 11 //头部添加元素 12 Link.addHead("clyang"); 13 Link.addHead(8848); 14 Link.addHead(true); 15 Link.toLinkString(); 16 17 //查找元素8848 18 boolean r=Link.find(8848); 19 System.out.println(r); 20 21 //更新元素 22 Link.modify(8848,"success people"); 23 Link.toLinkString(); 24 25 //删除元素 26 Link.delete("Messi"); 27 Link.toLinkString(); 28 29 } 30 }
控制台输出结果,发现可以正常表现为链表的功能。
双向链表的实现
参考博客,以及自己的理解,实现一个双向链表,同时可以保持链表的有序,可以根据索引来查找链表内容。
1 package DataCompose; 2 3 import java.util.Random; 4 5 /** 6 * 双向链表,自定义一个双向列表,具备增删改查和循环遍历的功能 7 */ 8 public class DoubleLinkTest { 9 //属性 10 private int size; 11 private Node head; 12 private Node tail; 13 14 15 //内部类,里面定义一个属性保存数据,再定义两个属性分别指向上一个节点以及下一个节点 16 private class Node { 17 //数据部分 18 private Object data; 19 //上一个节点和下一个节点的引用 20 private Node prev; 21 private Node next; 22 //序号部分 23 private int number; 24 25 //构造方法 26 public Node(Object data) { 27 this.data = data; 28 } 29 30 public Node(Object data, int number) { 31 this.data = data; 32 this.number = number; 33 } 34 } 35 36 //默认构造方法 37 public DoubleLinkTest() { 38 this.size = 0; 39 this.head = null; 40 this.tail = null; 41 } 42 43 //往头增加节点 44 public void addHead(Object obj) { 45 //往头部增加节点,默认索引号为-1 46 Node myNode = new Node(obj, -1); 47 //链表为空 48 if (size == 0) { 49 head = myNode; 50 tail = myNode; 51 head.number = 0; 52 tail.number = 0; 53 } else { 54 head.prev = myNode; 55 myNode.next = head; 56 //头节点重新赋值 57 head = myNode; 58 } 59 size++; 60 //刷新编号,所有索引号往后面移动一位 61 flushNumber(1); 62 //System.out.println("头部增加一个结点成功"); 63 } 64 65 //往尾部添加节点 66 public void addTail(Object obj) { 67 Node myNode = new Node(obj); 68 //链表为空 69 if (size == 0) { 70 tail = myNode; 71 head = myNode; 72 head.number = 0; 73 tail.number = 0; 74 } else { 75 tail.next = myNode; 76 myNode.prev = tail; 77 //尾部节点重新赋值 78 tail = myNode; 79 } 80 size++; 81 //尾部序号直接赋值,相比头部序号操作简单很多 82 tail.number = size - 1; 83 //System.out.println("尾部增加一个结点成功"); 84 } 85 86 //往链表内部,除了头部节点之前的任意一个结点插入新节点 87 public void add(Object obj) { 88 if (size == 0) { 89 addHead(obj); 90 } else if (size == 1) { 91 addTail(obj); 92 } else if (size >= 2) { 93 //根据链表中的现有长度,获取0~长度-1之间的随机数,将这个随机数作为要插入结点的前一个索引号 94 Random ran = new Random(); 95 int insertIndex = ran.nextInt(size); 96 //得到要插入位置的前后索引编号 97 int before = insertIndex; 98 int after = insertIndex + 1; 99 //如果before的索引已经达到链表末尾 100 if (before == size - 1) { 101 //尾部添加即可 102 addTail(obj); 103 } else { 104 //获取插入结点的前后结点 105 Node beforeNode = getNodeByIndexAndStartNode(before, head); 106 Node afterNode = getNodeByIndexAndStartNode(after, head); 107 Node startNode = afterNode; 108 //获取要插入的结点 109 Node currentNode = new Node(obj, after); 110 //重新连接前后结点 111 beforeNode.next = currentNode; 112 currentNode.prev = beforeNode; 113 afterNode.prev = currentNode; 114 currentNode.next = afterNode; 115 //序号更新,将后面一个结点的所有索引号+1 116 int startIndex = after; 117 while (startIndex <= size - 1) { 118 int newIndex = startNode.number + 1; 119 startNode.number = newIndex; 120 startNode = startNode.next; 121 startIndex++; 122 } 123 size++; 124 } 125 System.out.println("当元素大于或等于2个时,随机插入结点成功"); 126 } 127 } 128 129 //通过索引位置,找到对应的节点,另外第二个参数代表从头开始找还是从尾开始找 130 public Node getNodeByIndexAndStartNode(int index, Node node) { 131 if (index < 0 || index > size - 1) { 132 System.out.println("索引越界,无效索引"); 133 return null; 134 } else { 135 //当前结点 136 Node currentNode = node; 137 int count = size; 138 while (count > 0) { 139 if (currentNode.number != index) { 140 //区分node是从头开始还是从尾开始 141 if (node.equals(head)) { 142 currentNode = currentNode.next; 143 } else if (node.equals(tail)) { 144 currentNode = currentNode.prev; 145 } 146 } else { 147 break; 148 } 149 count--; 150 } 151 return currentNode; 152 } 153 } 154 155 //查找一个节点,可以使用二分查找,调用上面写的底层查找方法 156 public Node findNodeByIndex(int index) { 157 Node deleteNode=null; 158 if (size == 0) { 159 System.out.println("链表为空"); 160 return null; 161 } else { 162 if (index < size / 2) { 163 //从头开始寻找 164 Node node = getNodeByIndexAndStartNode(index, head); 165 //System.out.println(node.data); 166 deleteNode=node; 167 } else { 168 //从尾开始寻找 169 Node node = getNodeByIndexAndStartNode(index, tail); 170 //System.out.println(node.data); 171 deleteNode=node; 172 } 173 } 174 System.out.println(deleteNode.data); 175 return deleteNode; 176 } 177 178 //删除一个节点,根据链表中索引来删除 179 public boolean deleteNodeByIndex(int index) { 180 if (index < 0 || index > size - 1) { 181 System.out.println("下标越界,无法删除"); 182 return false; 183 } else { 184 //判断是否是首尾节点 185 if (index == 0) { 186 head = head.next; 187 size--; 188 //序号重置 189 flushNumber(-1); 190 } else if (index == size - 1) { 191 tail = tail.prev; 192 size--; 193 //依然从0开始,无需重置序号 194 } else { 195 //中间位置删除 196 Node beforeNode = findNodeByIndex(index - 1); 197 Node afterNode = findNodeByIndex(index + 1); 198 Node currentNode = findNodeByIndex(index); 199 //当前位置节点赋值为null,等待gc自动回收 200 currentNode = null; 201 //前后结点重新连接 202 beforeNode.next = afterNode; 203 afterNode.prev = beforeNode; 204 //重新设置后一个结点后面的索引号 205 Node startNode=afterNode; 206 int startIndex=startNode.number; 207 while(startIndex<=size-1){ 208 int newIndex=startNode.number-1; 209 startNode.number=newIndex; 210 startNode=startNode.next; 211 startIndex++; 212 } 213 size--; 214 } 215 return true; 216 } 217 } 218 219 //修改一个节点内容 220 public boolean modify(int index, Object obj) { 221 if (index < 0 || index > size - 1) { 222 System.out.println("索引越界,无效索引"); 223 return false; 224 } else { 225 Node currentNode = findNodeByIndex(index); 226 currentNode.data = obj; 227 System.out.println("修改成功"); 228 return true; 229 } 230 } 231 232 //遍历节点 233 public void toDoubleLinkArray() { 234 if (size > 0) { 235 if (size == 1) { 236 System.out.println("[" + "(" + head.data + ":" + head.number + ")" + "]"); 237 return; 238 } 239 //依然从头部开始遍历 240 Node currentNode = head; 241 int count = size;//需要遍历的次数 242 while (count > 0) { 243 if (currentNode.equals(head)) { 244 System.out.print("[" + "(" + currentNode.data + ":" + currentNode.number + ")"); 245 } else if (currentNode.next == null) { 246 System.out.print("--->" + "(" + currentNode.data + ":" + currentNode.number + ")" + "]"); 247 } else { 248 System.out.print("--->" + "(" + currentNode.data + ":" + currentNode.number + ")"); 249 } 250 //每输出一个往后移动一个节点 251 currentNode = currentNode.next; 252 count--; 253 } 254 //换行 255 System.out.println(); 256 } else { 257 System.out.println("[]"); 258 } 259 } 260 261 //更新所有节点顺序编号,往前或者后移动一位 262 public void flushNumber(int number) { 263 if (size > 1) { 264 int count = size; 265 Node currentNode = head; 266 while (count > 0) { 267 if (number != 1&&number != -1) { 268 System.out.println("移动数字非法"); 269 return; 270 } else { 271 if (number == 1) { 272 int newNumber = currentNode.number + 1; 273 currentNode.number = newNumber; 274 } else if(number==-1){ 275 int newNumber = currentNode.number - 1; 276 currentNode.number = newNumber; 277 } 278 currentNode = currentNode.next; 279 count--; 280 } 281 } 282 System.out.println("链表序号刷新完成"); 283 } else { 284 System.out.println("链表为空,或者无需刷新节点编号"); 285 } 286 } 287 288 }
测试代码
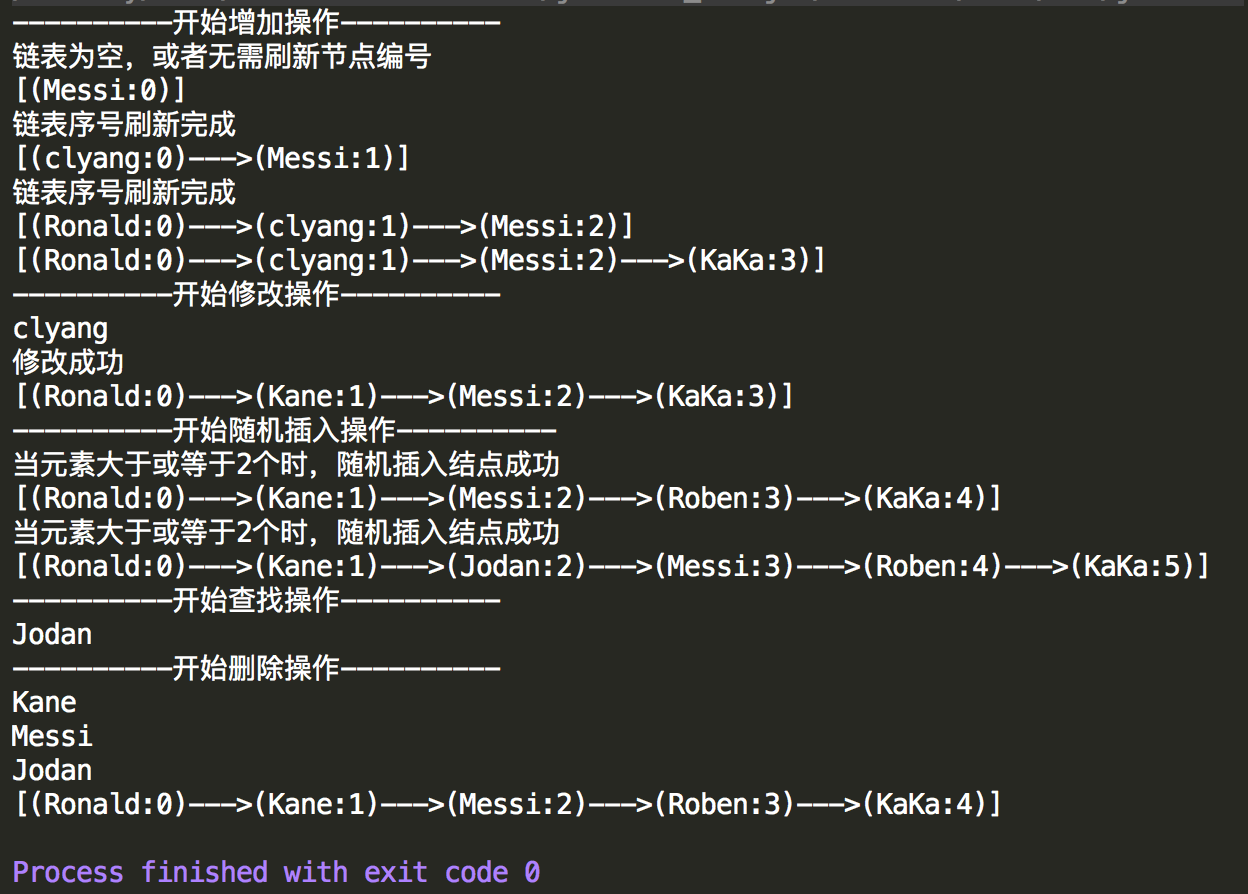
1 package DataCompose; 2 3 public class TestDoubleLinkTest { 4 5 public static void main(String[] args) { 6 //测试双向链表 7 DoubleLinkTest Link=new DoubleLinkTest(); 8 //添加 9 System.out.println("----------开始增加操作----------"); 10 Link.addHead("Messi"); 11 Link.toDoubleLinkArray(); 12 13 Link.addHead("clyang"); 14 Link.toDoubleLinkArray(); 15 16 Link.addHead("Ronald"); 17 Link.toDoubleLinkArray(); 18 19 Link.addTail("KaKa"); 20 Link.toDoubleLinkArray(); 21 22 System.out.println("----------开始修改操作----------"); 23 //修改位置1的元素 24 Link.modify(1,"Kane"); 25 Link.toDoubleLinkArray(); 26 27 System.out.println("----------开始随机插入操作----------"); 28 //随机插入一个结点 29 Link.add("random"); 30 Link.toDoubleLinkArray(); 31 32 //再次随机插入一个结点 33 Link.add("Jodan"); 34 Link.toDoubleLinkArray(); 35 36 System.out.println("----------开始查找操作----------"); 37 //查找位置为2的节点 38 Link.findNodeByIndex(2); 39 40 System.out.println("----------开始删除操作----------"); 41 //删除节点2的位置 42 Link.deleteNodeByIndex(2); 43 Link.toDoubleLinkArray(); 44 } 45 46 }
控制台输出情况,可以正常的实现增删改查循环遍历的功能,并且插入删除后依然可以保证节点的顺序。
红黑树
树型数据结构
树形结构名词介绍,比较形象,类似于现实中的树,只是计算机中的树其根部在上面,叶子在下面。
结点:树中的一个元素
结点的度:结点拥有的子树的个数,二叉树的话,度不能大于2
高度:叶子节点的高度为1,逐渐往上越来越高,根节点高度是最高的
叶子:高度为0的结点,也是终端结点
层:以根开始是第一层,往下面开始逐一增加
父结点:若一个结点包含若干个子结点,则这个结点就是子结点的父结点
子结点:子结点就是父节点的下一个节点
结点的层次:以根节点开始,根节点为第一层,根的子结点为第二层,逐一类推
兄弟结点:拥有共同父结点的结点称为兄弟结点
平衡因子:该结点左子树的高度-该结点右子树的高度,即平衡因子
二叉树(binary tree)
是每个结点不超过2个子结点的有序树(tree),每个结点上最多只能有两个子结点,顶上的结点叫做根结点,两边的分支分别叫做左子树和右子树。
平衡树
也是基于二叉树,平衡因子的绝对值不能超过1,即左右子树高度差不能达到2。当往父结点上添加一个子结点后破坏了平衡条件,就会进行平衡旋转,有LL、LR、RR和RL四种类型的平衡旋转,为了想看动画演示旋转,可以登录后面参考的网址(https://www.cs.usfca.edu/~galles/visualization/AVLtree.html)即可。
(1)LL型平衡旋转
如果往如图所示的结点6下面再添加一个子结点4,可以分析一下各个结点的平衡因子,叶子结点4的平衡因此为0,父结点6的平衡因子为1,根结点8的平衡因子为2,破坏了二叉树的平衡条件,因此需要右旋,即6上升到根结点,8移动到根结点的右边,作为子结点。
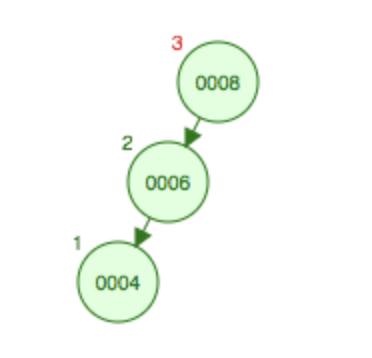 旋转后
旋转后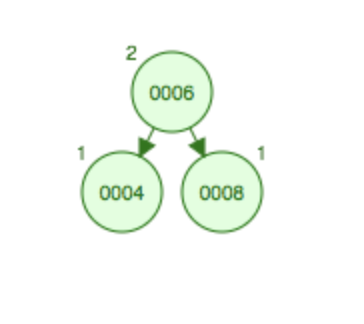
(2)LR型平衡旋转
同样在结点6的下面增加一个子结点7,添加后在6子结点的右边,其平衡依然被破坏,因此也需要旋转,首先7结点的位置会移动到6的位置,6的位置移动到7的左子结点,这个过程为左旋,变成6-7-8的LL型,然后再右旋转,将7上升到根节点,8变成根结点的右结点。
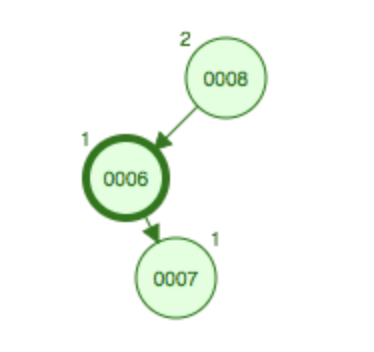 旋转后
旋转后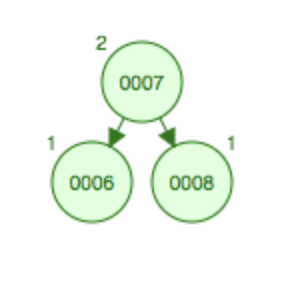
(3)RR型平衡旋转
在父节点10的下面添加一个子结点12,也破坏了平衡性,因此需要左旋,即10上升到根结点的位置,8变成根节点的左子结点。
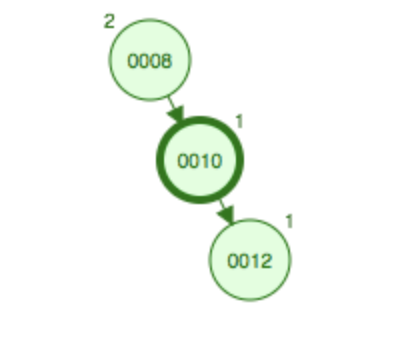 左旋转
左旋转 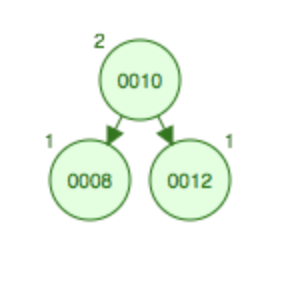
(4)RL型平衡旋转
在父节点10下面添加子结点9,发现比10小因此为左子结点,与上面情况类似,添加子结点后依然破坏了平衡性,因此需要旋转,首先需要右旋转将9上升到父节点10的位置,将10变成9的右子结点,即变成10-9-8的RR型,这样还需要进行一次左旋转,将9上升到根结点的位置,原根结点8变成9的左子结点。
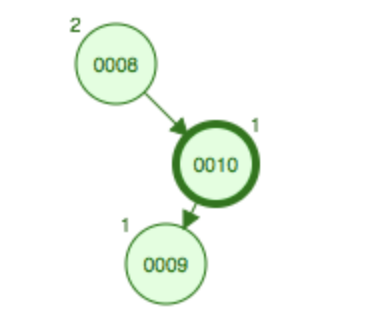 旋转后
旋转后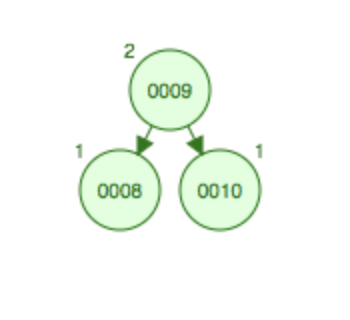
旋转实战演练,先在左子树添加元素,先调整成LL型,然后右旋
往下面平衡树下添加子结点4,可以分析一下,4比20小,往左边子树走,然后比5小,依然往左边子树走,最后到了字结点2,发现比2大因此挂在了2的右子结点,这样显然是破坏了二叉树的平衡的。因此随后需要对2-4-5三个结点进行LR平衡型旋转,首先2左旋,将4移动到2结点的位置,2变成4结点的左子结点,这样就变成了2-4-5的LL型,然后右旋,将4上升到父结点5的位置,而5变成4的右子结点。
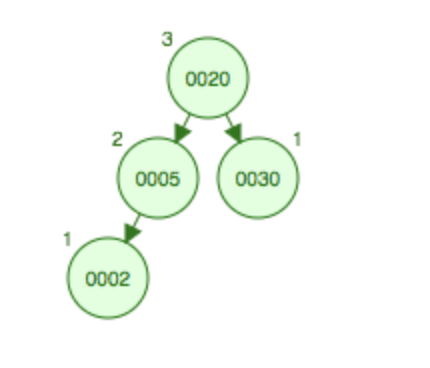 添加4后
添加4后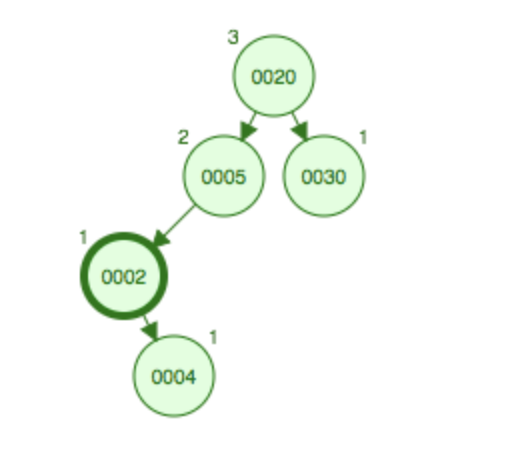 先左旋后右旋
先左旋后右旋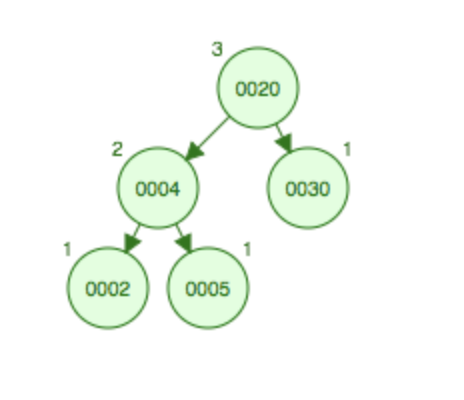
如果继续在上面二叉树的基础上在添加字结点1,显然会破坏平衡,因此4需要上升为根节点,将20进行右旋,20右旋会跟4的右结点5发生碰撞,这种情况就将5挂到20的左边,达到平衡。
 右旋转
右旋转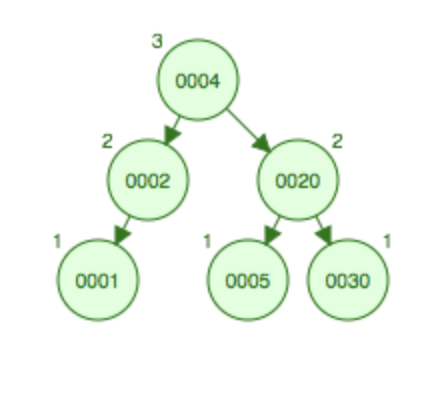
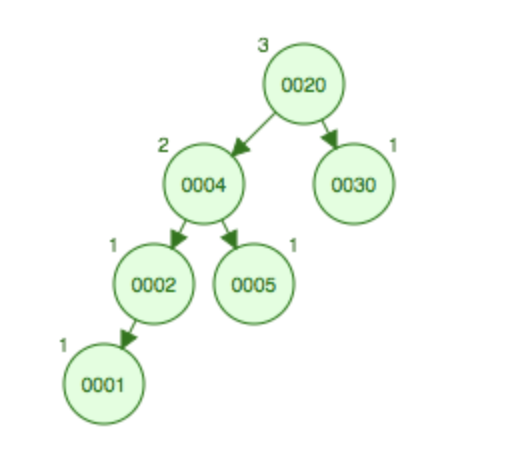
如果要在如图所示的树上增加结点6,需要先左旋变成LL型,将7移动到父节点5的位置,5移动到7的左节点,这个时候5和6会发生碰撞,将6挂到5结点的右边,变成LL型,然后将7上升到根结点,然后进行右旋,将20和30都挂到7的右边。
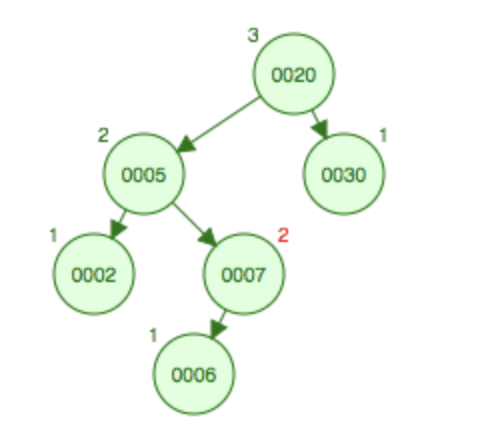 先左旋后右旋
先左旋后右旋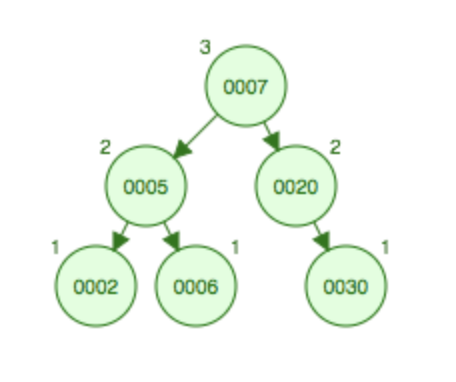
如果在如图所示的树上添加8,依然先需要进行左旋变成LL型,将7上升到父结点5的位置,5和2变成7的左子树,8变成7的的右结点,然后进行右旋,将7上升到根结点的位置,这样20和8都为7的右结点会发生碰撞,将8挂到20的下面。
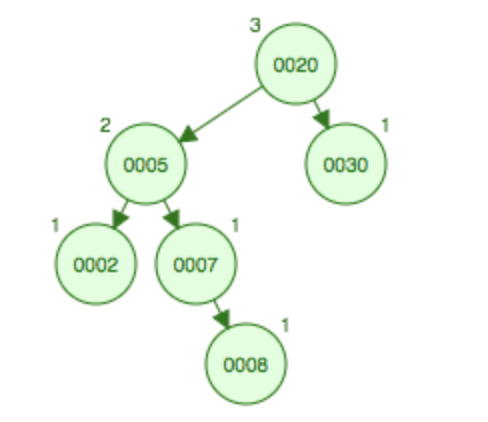 先左旋后右旋
先左旋后右旋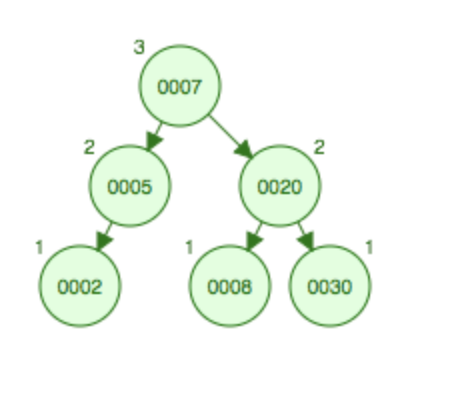
旋转实战演练,在右子树添加元素,先调整成RR型,然后左旋
如果在二叉树中添加结点60,破坏了二叉树的平衡,由于右子树已经是RR型,因此需要左旋就行,30左旋变成50的子结点,50上升到原先30的位置。
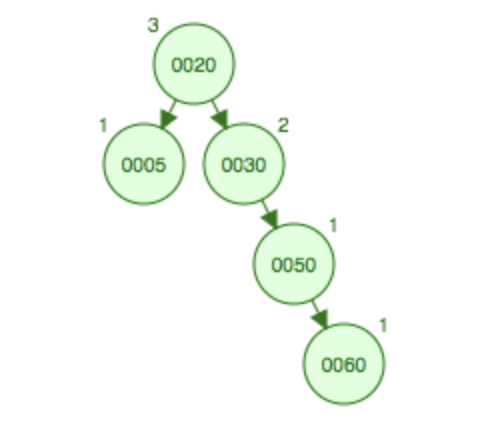 左旋
左旋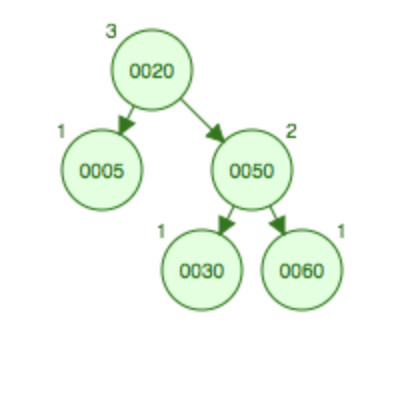
继续在上面的二叉树上添加结点70,发现右边也已经是RR型,无需调整,只要将50上升到根结点,将20结点进行左旋即可,左旋后20和30会发生碰撞,由于30比20大因此及会挂在20的右边。
 已经是RR型,直接左旋
已经是RR型,直接左旋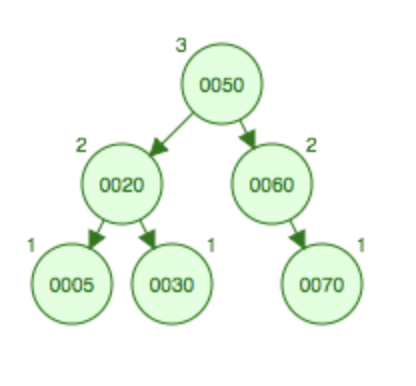
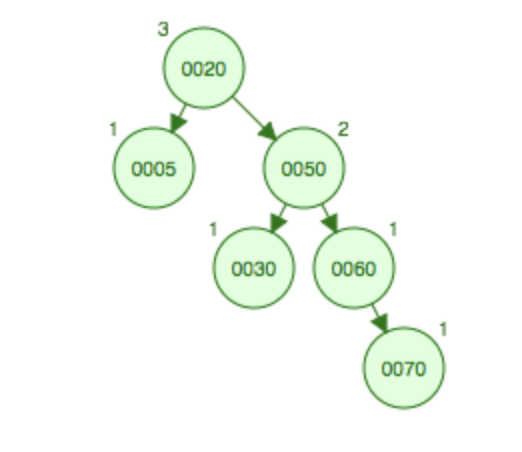
如果不在50结点上添加子结点,在25结点上添加一个右子节点,会稍微复杂一点,首先需要将右子树变成RR型,需要先右旋一次,将25上升到30父节点的位置,30变成25的右边子结点,这样30和28会发生碰撞,由于28比30小因此变成其左子结点,这样右边变成RR型,然后将20根结点进行一次左旋,就达到平衡。
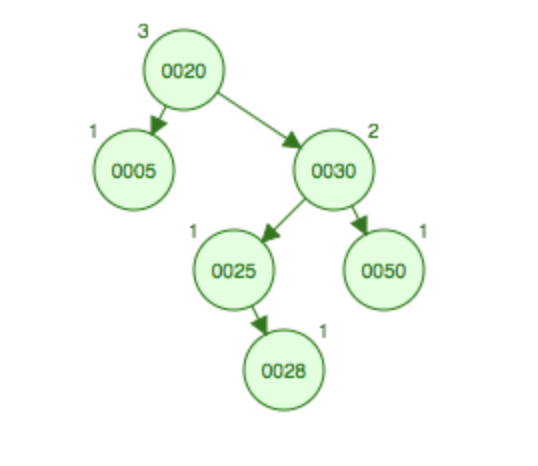 先右旋变成RR型,然后左旋
先右旋变成RR型,然后左旋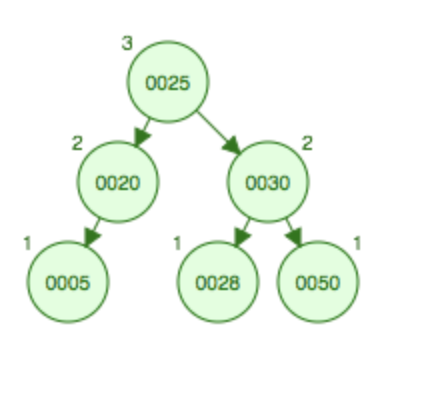
如果不在50结点上添加子结点,在25结点上添加一个左子节点,依然需要先将右子树进行右旋,这样25上升到30的位置,25父节点下面左子结点为23,右子树为30和50,这样变成RR型,然后将20左旋,这样20和23会发生碰撞,由于23比20大因此会挂到20的右边,达到平衡。
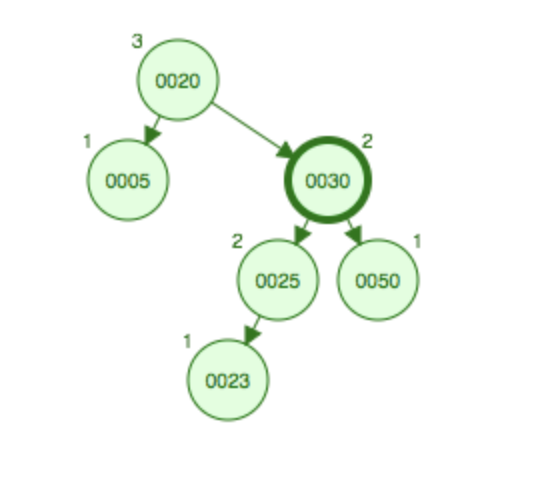 先右旋变成RR型,然后左旋
先右旋变成RR型,然后左旋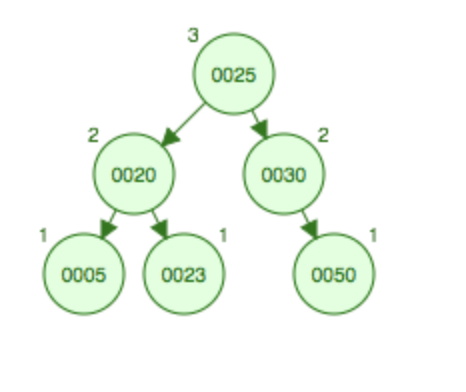
不平衡树
基于二叉树,左子树和右子树数量不相等,在极端情况下可能导致查询变成类似查询链表的情况。
排序树/查找树
排序树是基于二叉树,左子树数值小,右子树数值大,查找数字会很快。
红黑树
红黑树(Red Black Tree)是一种自平衡二叉查找树,在1972年由Rudolf Bayer发明,称为平衡二叉B树,后面被修改为红黑树,红黑树是一种特殊的二叉查找树,其每个节点不是红就是黑。其查找叶子节点的最大次数和最小次数不能超过2倍,跟平衡二叉树不太一样的是,它不需要满足平衡因子绝对值<=1。
红黑树还有以下约束:
1 节点可以是红色或者黑色的
2 根节点是黑色的
3 叶子节点(NIL节点,空节点)是黑色的
4 每个红色节点的子节点都是黑色,即每个叶子到根的路径上不会存在两个连续的红色节点
5 任何节点,到其下面每一个叶子节点的路径上,黑色节点数是相同的
黑红树的主要用途就是使用在HashMap,TreeMap中。
红黑树左旋右旋
红黑树的左旋和右旋,可以参考上面平衡二叉树的左旋和右旋规律,基本一样。
红黑树的插入操作
红黑树如果做插入结点操作,会改变原始红黑树的结构,一般插入的是红色结点,并且有相应的恢复策略,参考了哔哩哔哩视频(https://www.bilibili.com/video/av53772633/?p=3&t=275),大致上可以按照以下的规则来,但是红黑树还有自己的约束,因此个人感觉可以将下面的规则做为参考,但是不一定实际中完全适用,如约束中的第5条,就会导致下面部分规则不完全适用。
(1)插入的是根结点
原始树是空树,因此根节点为红色,违反上面约束条件第二条
策略:将结点涂成黑色
(2)插入结点父结点是黑色
策略:红黑树没有破坏,不需要修复
(3)插入结点后,当前结点的父结点是红色,并且叔叔结点也是红色。
策略:当前结点'4'的父结点'5'和叔叔结点'8'全部变成黑色,祖父结点'7'变成红色。
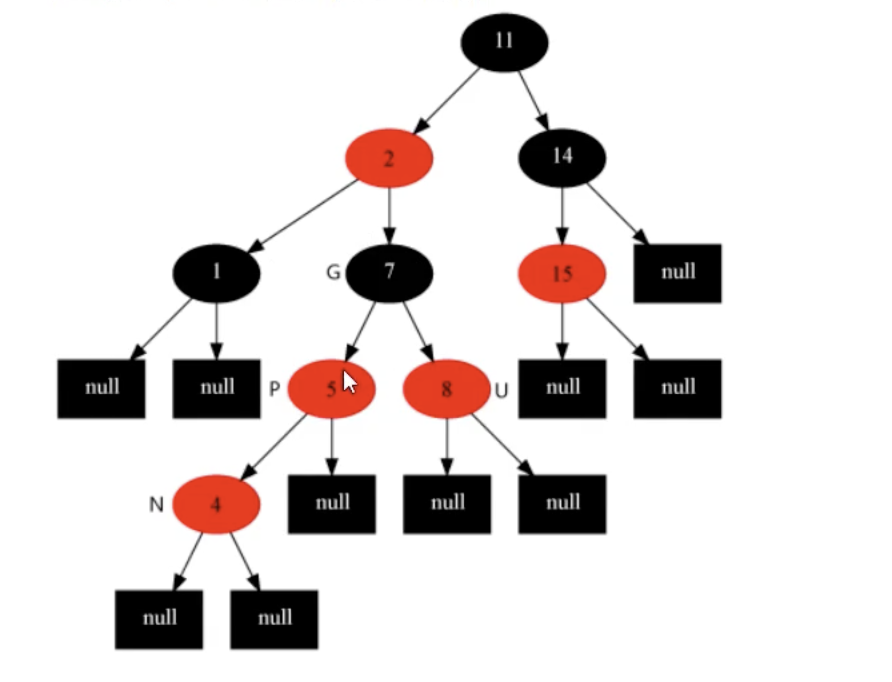 变化后
变化后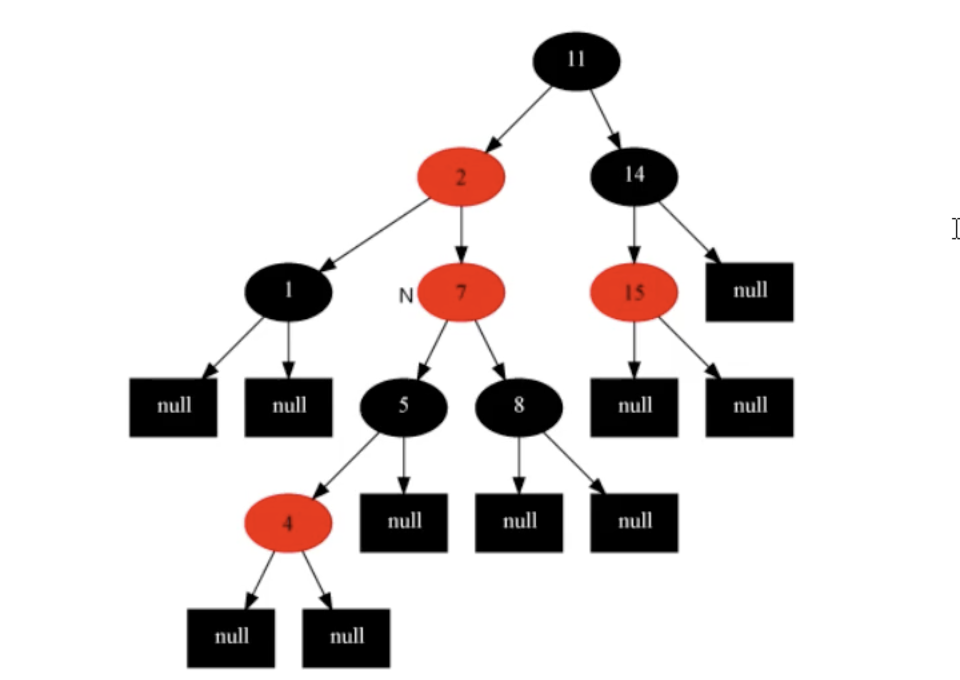
(4)当前结点的父结点是红色,叔叔结点是黑色,并且当前结点是父结点的右结点。
策略:当前结点'7'的父结点'2'为支点左旋,当前结点'7'上移动。如果当前结点是父结点的左结点,后面再补充。如图'2'和'5'的结点左旋会发生碰撞,由于'5'比'2'大因此将'5'结点对应的子树挂在结点'2'的右子树。
 左旋
左旋
(5)当前结点的父结点是红色,叔叔结点是黑色,当前结点是父结点的左结点
策略:当前结点'2'的父结点'7'变成黑色,祖父结点'11'变成红色,以祖父结点'11'为支点进行右旋。右旋时'11'和'8'会发生碰撞,由于'8'比'11'小因此'8'结点对应子树挂在'11'结点的左边作为左子树。
 变色以及右旋
变色以及右旋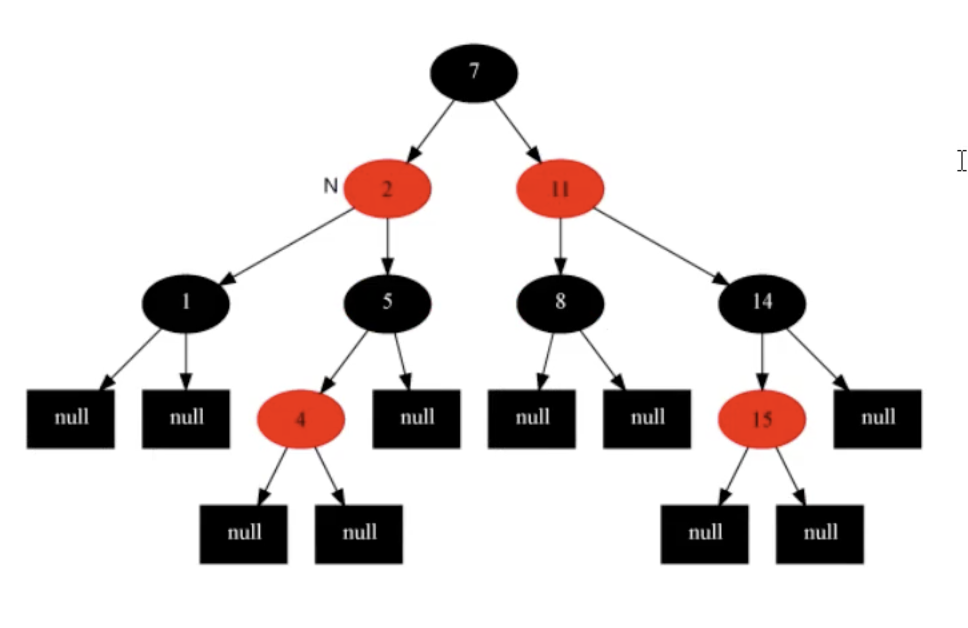
红黑树添加结点实战演练
如图在红黑树的结点上添加20,刚开始作为50的左子结点,这样不符合红黑树的规则,并且这样的情况满足上面说的情况5,因此50结点会变成黑色,根结点右旋。根据动画可以看出来,先完成右旋,再完成变色。
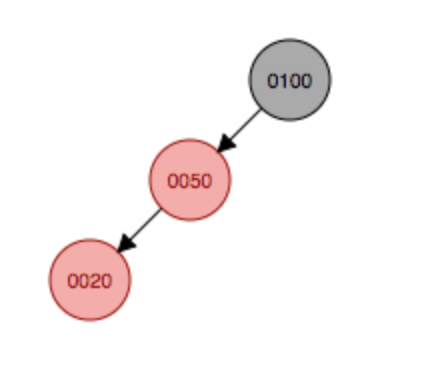 旋转
旋转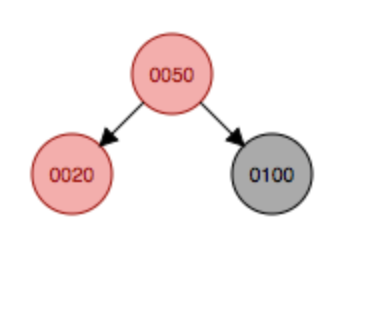 变色
变色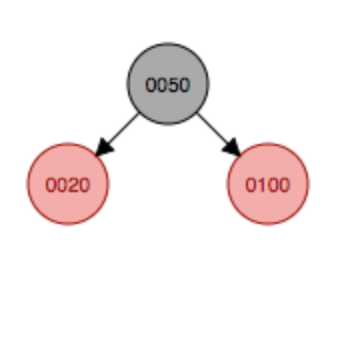
继续添加结点200,首先会作为100的右结点添加,这种符合上面说的情况3,因此父结点和叔叔结点都变成黑色,祖父结点50变成红色,然后根节点不能为红色,因此继续变色,最后根节点变成黑色。需要注意的是红色节点的子结点必须为黑色节点,但是没有规定黑色节点的子结点必须为红色,说明黑色节点下面子结点什么颜色都可以。
 变色
变色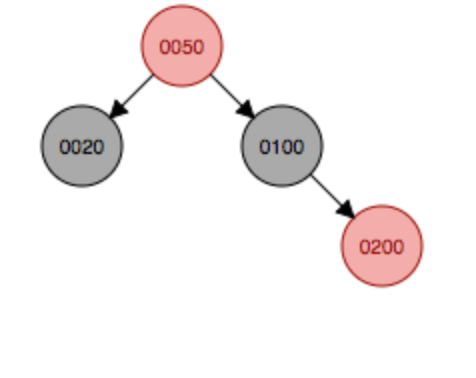 继续变色
继续变色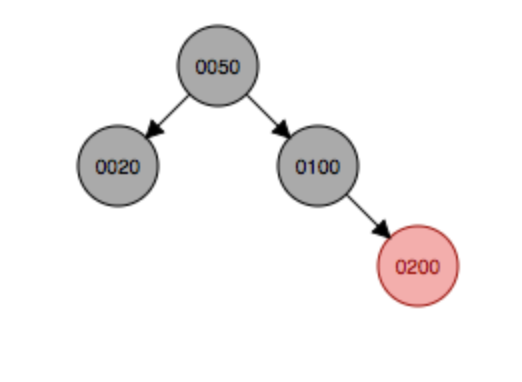
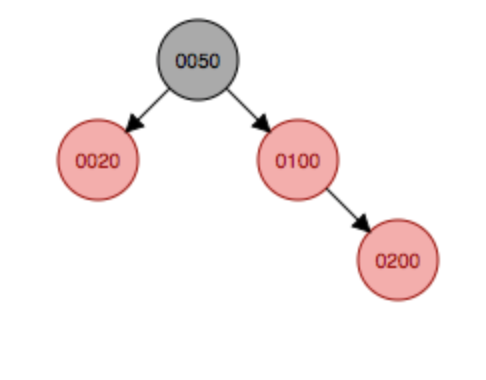
继续添加结点300,首先会作为子结点添加到200的右子结点,这种符合上面说的情况5,因此首先以插入结点的祖父结点100为支点发生左旋,然后变色,父结点200变成黑色,原祖父结点变成红色。
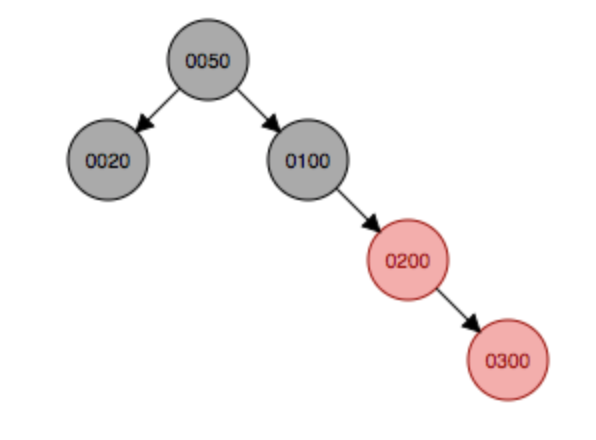 左旋
左旋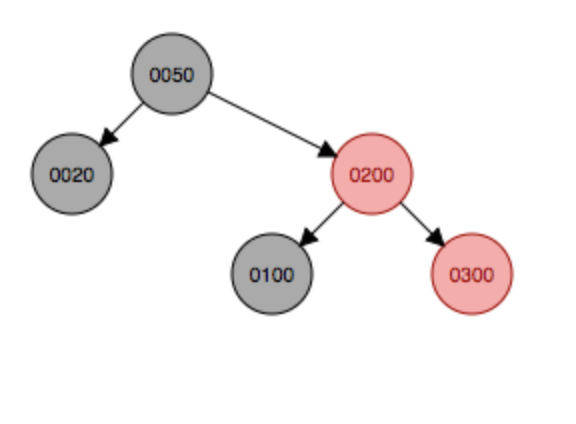 变色
变色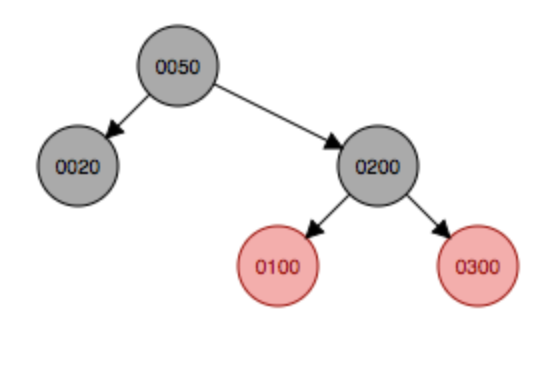
继续添加结点150,首先会作为子结点添加到100的右子结点,这种符合上面的情况3,因此父结点和叔叔结点变成黑色,祖父结点200变成红色,变完色后发现符合黑红树规则,无需再旋转或变色。
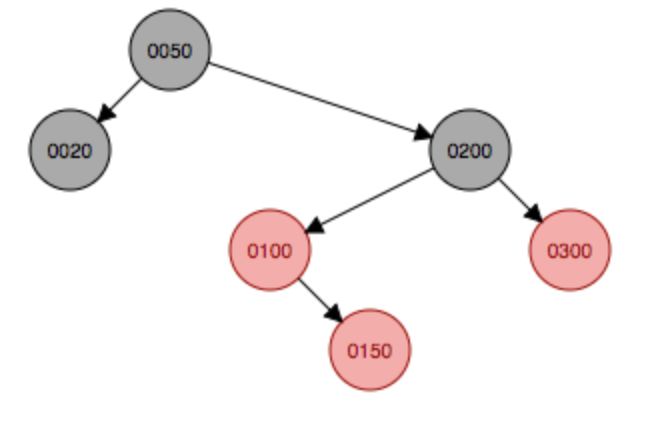 变色
变色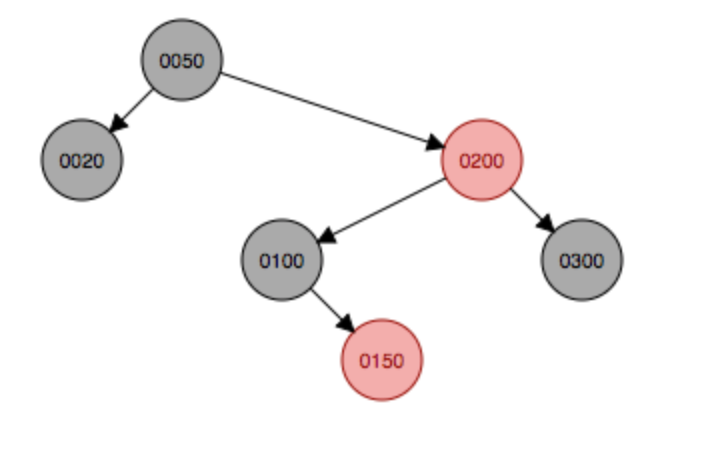
继续添加元素160,会先作为右结点挂在150下面,然后这种情况符合上面第五种,因此先按照祖父结点100为支点左旋,然后父结点变成黑色,原祖父结点变成红色,完后发现符合黑红树规则,无需再选择或变色。
 左旋
左旋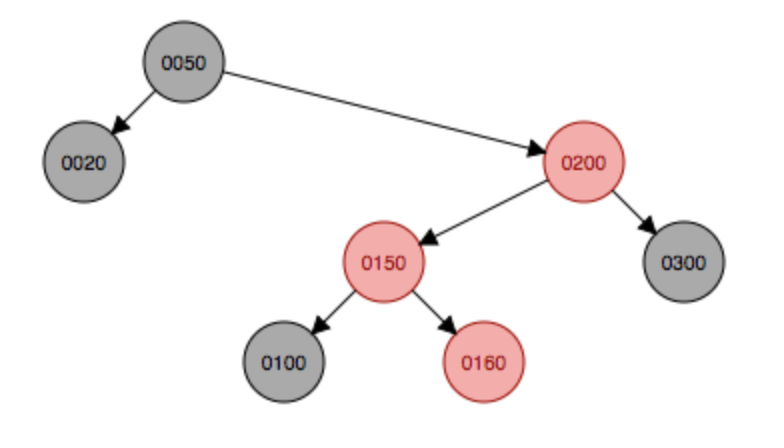 变色
变色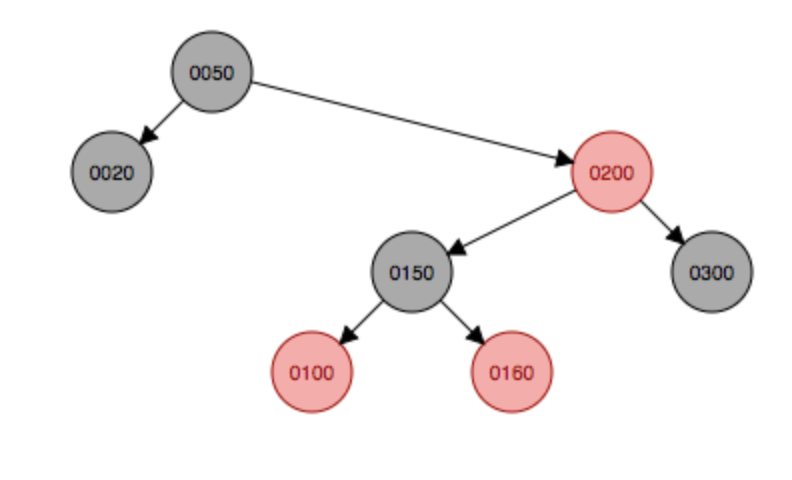
添加320到子结点,会首先挂在350下面,然后这种符合第四种情况,父结点是红色,叔叔结点(null)为黑色,由于当前结点在父结点的左边,因此先以父结点350为支点右旋,右旋后变成上面的第五种情况,因此先以祖父结点300左旋,然后父结点320变色为黑色,原祖父结点300变色为红色。
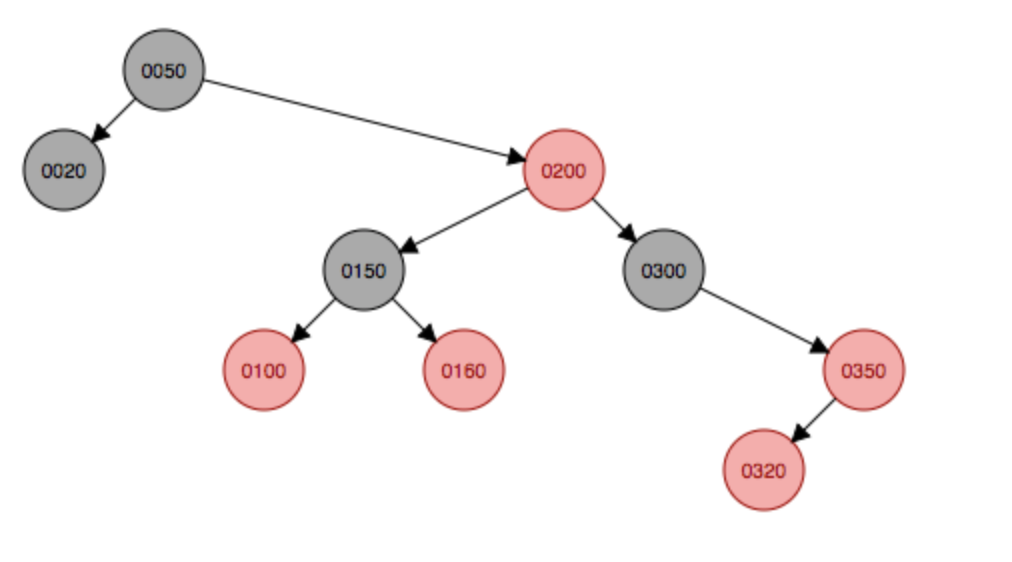 右旋
右旋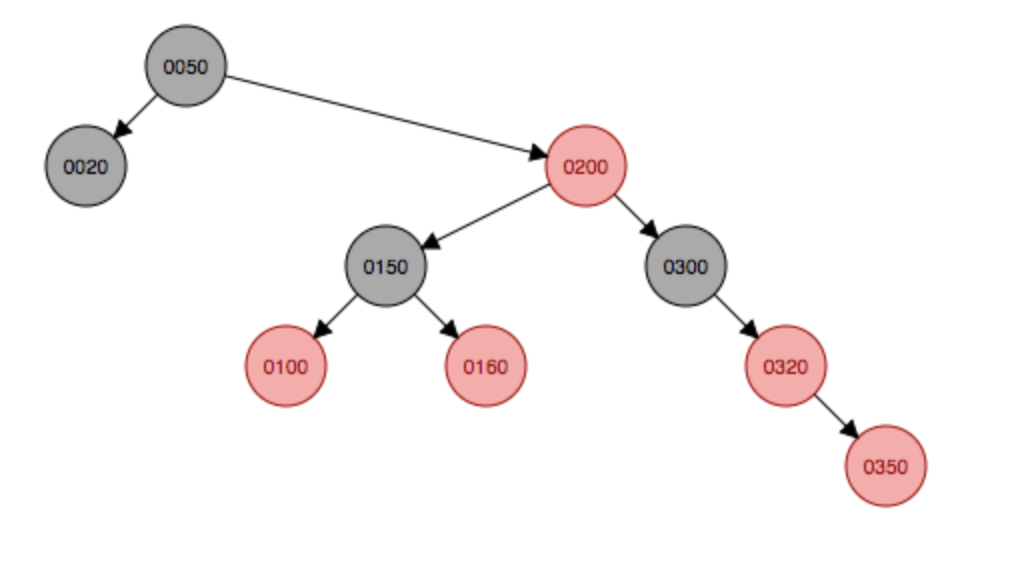 左旋变色
左旋变色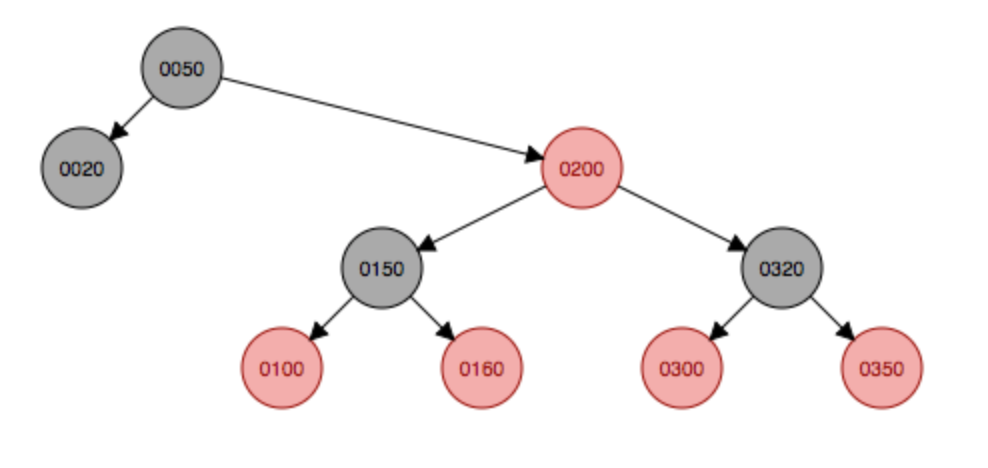
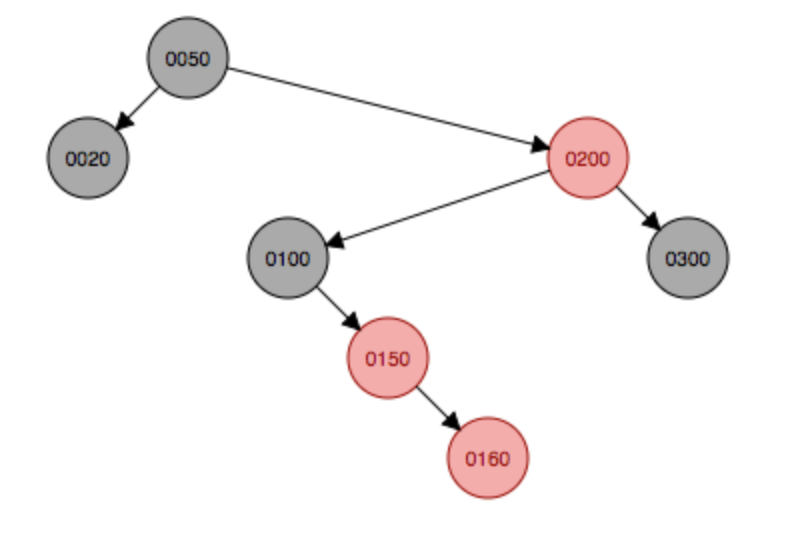
最后添加180到结点中,这个添加会将上面说的第三四五种情况都包含,首先添加到160的右子结点,这种符合第三种情况,因此父结点和叔叔结点都变色为黑色,祖父结点150变成红色。
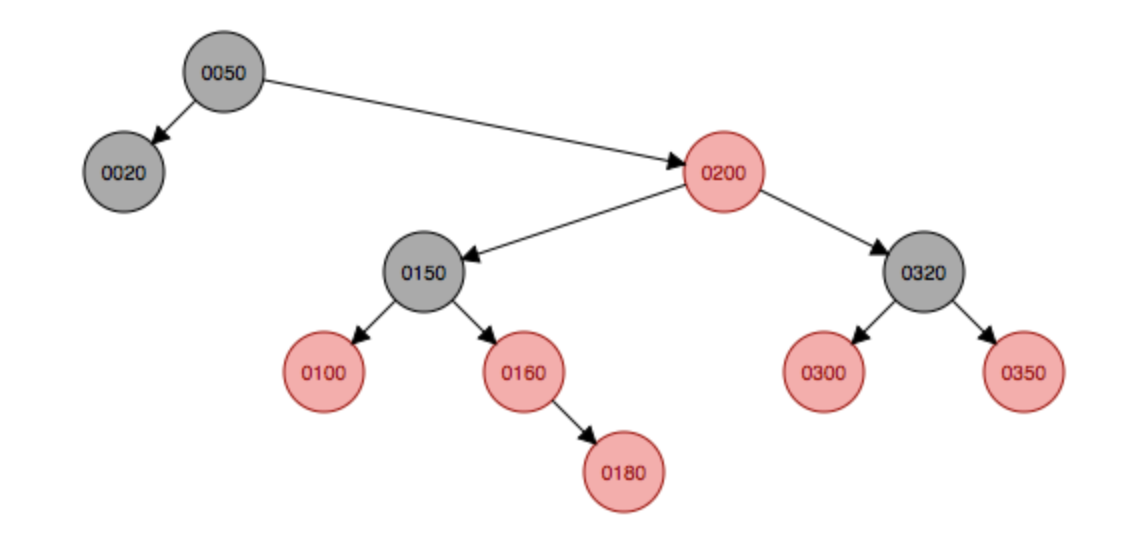 变色
变色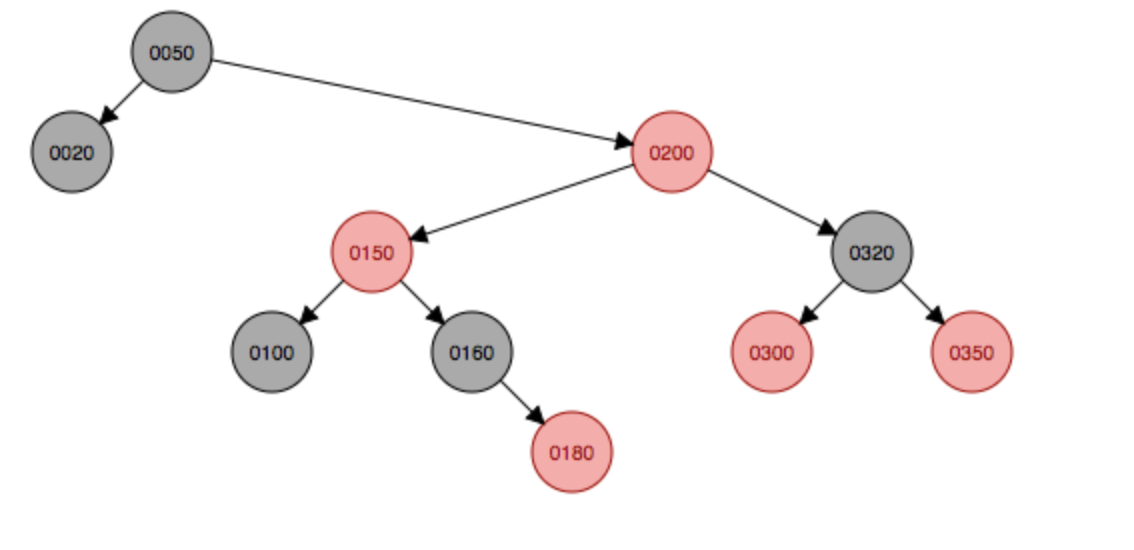 右旋
右旋
变成红色后,这种为第四种情况,即150结点的父结点是红色,叔叔结点是黑色,因此本例中需要右旋,由于右旋后200和160会碰撞,因此160结点的子树将作为200结点的左子树。
 左旋
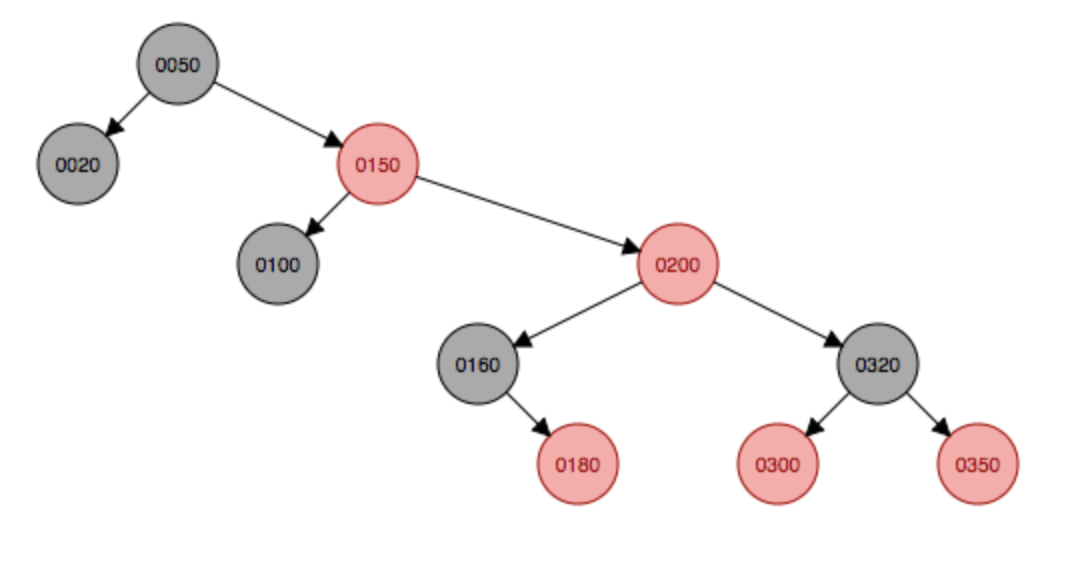
左旋
然后变成了第五种情况,只是在右边,因此需要以200结点的祖父结点50为支点左旋,由于左旋后,50和100会发生碰撞,因此100将挂在50结点的右边。并且父结点150变成黑色,祖父结点50会变成红色。
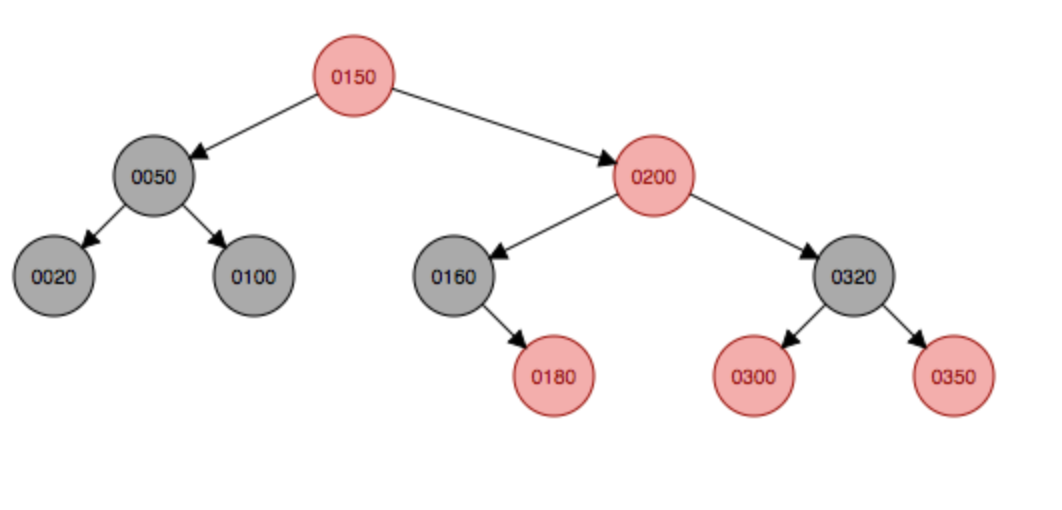 变色
变色
关于红黑树的删除结点后面再添加,后续完善。
总结
以上是对数据结构基础的复习和理解,包括栈、队列、数组、链表和红黑树,还有很多理解不到位的地方,后续工作和学习中再补充添加,感谢引用的各位博文博主。
参考博文:
(1)《Java核心技术卷》第8版
(2)https://www.cnblogs.com/ysocean/p/7911910.html 栈
(3)https://www.cnblogs.com/youngchaolin/p/10463887.html 二进制
(4)https://segmentfault.com/a/1190000016524796 队列
(5)https://www.cnblogs.com/ysocean/p/7894448.html 数组
(6)https://www.cnblogs.com/ysocean/p/7928988.html 链表
(7)https://www.cnblogs.com/shamo89/p/6774080.html 队列
(8)https://www.cnblogs.com/ChenD/p/7814906.html 双向链表
(9)https://segmentfault.com/a/1190000014037447?utm_source=tag-newest 红黑树
(10)https://www.cs.usfca.edu/~galles/visualization/AVLtree.html 生成平衡二叉树动画
(11)https://www.cs.usfca.edu/~galles/visualization/RedBlack.html 生成红黑树动画
(12)https://www.cnblogs.com/lezhifang/p/6632355.html 平衡二叉树旋转



 浙公网安备 33010602011771号
浙公网安备 33010602011771号