二进制学习
二进制是计算机的基础,计算机只识别二进制数据,其基础运算是采用2进制。编程语言写好的程序经过编译后变成计算机能识别的2进制数据,人不可能直接写2进制数据,其中间需要通过编程语言进行协调,所以编程语言就是连接人类和计算机之间的桥梁,下面补充学习二进制基础知识。
二进制
(1)计算机内部只有2进制数据,别的一概没有。Java编程语言,利用算法支持10进制,使用户感受上可以使用10进制,比如System.out.println(50)运行输出了50,其实其底层调用了Integer.toString()方法进行了转换,将2进制110010转换成10进制50。底层算法是如下方法:

(2)Java底层是有方法实现2进制数据和10进制数据的相互转换,具体如下:
将10进制字符串转换为2进制int ---->Integer.parseInt()
将2进制int转换为10进制的字符串 ---->Integer.toString()
了解2进制规则时,需要配套了解16进制规则,因为两者可以相互转换,4位2进制可以简写为一个16进制数,可以通过排列组合就可以理解了。
(3)2进制规则:
①逢二进一的计数规则,可以参考只有2个算珠的算盘,移动算珠到上面代表0位,移动算珠下来代表1位
②权:64,32,16,8,4,2,1 (1的2倍数)
③基数:2
④数字:01
(4)16进制规则:
①逢十六进一的计数规则
②权:256,16,1(1的16倍数)
③基数:16
④数字:0123456789abcdef
二进制补码
计算机用来处理(有符号数)负数问题的算法
补码算法:位数补码
①总的位数是4位数
②如果计算结果超过4位数,自动溢出舍弃
先来看看只有4位的2进制数,发现范围是从0000~1111,代表10进制的0~15,如果1111加1,会变成10000,超过4位,最高位1自动溢出舍弃,变成0000,发现又回到起点,所以如果只是4位的2进制数字,采用补码规则,最多只能表示16个数,现在前人根据这样,将2进制高位为0的分成1半,2进制高位为1的分成1半,前者用来表示正数,代表0~7,后者用来表示负数,代表-1~-8。具体参考如下图片:
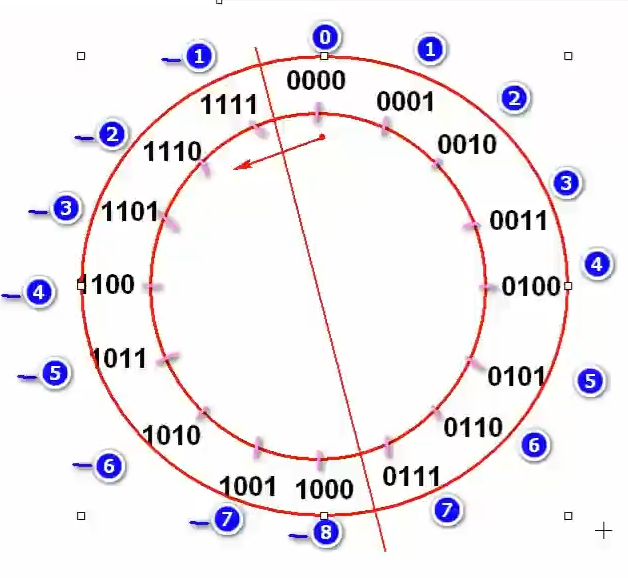
其中0~7的对应的2进制数为0000~0111,其中-1~-8的对应2进制数为1111~1000,其实计算机原本只有正数,-1~-8的这几个,在计算机底层还是正数,通过算法Integer.toString(),变成负数展示给人看,让人感觉好像有负数,上面通过4位来表示一个数,取值范围就是-2^3~2^3-1 ,这些数是完全不能满足生活需求的,因此就扩大了位数,用来展现更多的数字,就有了如下几种数据类型:
①byte,通过8位来表示一个数,取值范围为-2^7~2^7-1,取值范围-128~127,单位为1个byte,即一个字节
②short,通过16位来表示一个数,取值范围为-2^15~2^15-1,取值范围-32768~32767,单位为2个字节,即2byte
③带符号int,通过32位来表示一个数,取值范围为-2^32~2^31-1,取值范围-2147483648~2147483647,单位为4个字节,即4byte
④无符号int,也是32位,取值范围0~2^32-1
⑤long,通过64位来表示一个数,取值范围-2^63~2^63-1,取值范围-9223372036854774808~9223372036854774807,单位为8个字节,即8byte
以下为浮点型:
(1)float,4byle,32位
(2)double,8byte,64位
字符型:
(1) char,2个字节,16位
布尔型:
(1)boolean,可能就是一个bit,也可能是一个byte
互补对称公式:-n=~n+1,意思就是一个数对应的另外一个符号对称数,等于2进制位数取反后加1。可以参考上图圆盘就一目了然。
@Test
public void testBinary8() {
/**
* 测试互补对称公式 -n=~n+1
*/
System.out.println(~8+1);//-8
System.out.println(Integer.toBinaryString(~8+1));//11111111111111111111111111111000
System.out.println(~8);//-9
System.out.println(Integer.toBinaryString(~8));//11111111111111111111111111110111
System.out.println(~-8);//7
System.out.println(Integer.toBinaryString(~-8));//111
System.out.println(~-8+1);//8
System.out.println(Integer.toBinaryString(~-8+1));//1000
}
二进制运算符
① ~ 取反
② & 与运算 主要用于截取
0&0=0
0&1=0
1&0=0
1&1=1
③ | 或运算 主要用于合并
0|0=0
0|1=1
1|0=1
1|1=1
④ >>> 逻辑右移动运算
将二进制数值总体往右边移动一定位数,低位溢出不要,高位不够用0补齐
比如 n=00000000 00000000 00000000 11010001
m=n>>>1运算后
变成 (0)00000000 00000000 00000000 1101000(1)
整体往右边移动了1位,低位的1去掉,高位补上0,变成如下形式:
000000000 00000000 00000000 1101000
⑤ >> 数学右移动运算
⑥ << 数学左移动运算
编码方案
字符是16位的,而流(文件/互联网)按照byte(8位)进行处理,将文字进行传输必须拆分为byte,这个拆分方法,成为文字的编码。把文字拆开,变成8位8位的格式,即编码,反过来叫做解码。
编码方案学习:
首先需要了解一下几个概念,unicode,ASCII,UTF-8之间到底有啥区别?
unicode:一个字符对应一个数,就是将全世界所有知道的字符统计进去,目前到了10万+
UCS unicode3.2标准 0~65535 java char就是这个UCS
UTF-8:变长编码,1-4字节,短的1字节,长的4字节,具体有以下几种:
① 0~127 1字节编码,这个范围的也叫做ASCII码,主要显示英文和其他西欧语言,格式为 0XXXXXXXX
② 128~2048? 2字节编码,格式为110XXXXX 10XXXXXX
③ 2048?~65535 3字节编码,中文,韩文日文等都在这个范围内,格式为1110XXXX 10XXXXXX 10XXXXXX
④ 65535~10万 4字节编码,格式11110XXX 10XXXXXX 10XXXXXX 10XXXXXX
比如'中'这个字符,对应的unicode编码为0x4e2d,转化成二进制为0100 1110 0010 1101
然后需要使用三个字节编码,将二进制格式按顺序填充到格式1110XXXX 10XXXXXX 10XXXXXX中,变成11100100 10111000 10101101,这个就是UTF-8编码,所以将字符的unicode索引添加到UTF-8的字节位置上,叫做编码,然后网络通过8位一个字节一个字节的传输,然后如果将网络上传输的字节一个一个的组合起来,反过来从其中取出对应位置的的数,再和unicode索引对照找到对应的字符,这个过程就做解码。
编码实例分析
接下来用'中'字符进行编码 中字符 unicode编码为:0100 1110 0010 1101 ,在java中会将前面的位补齐,变成如下形式
00000000 00000000 01001110 00101101
然后需要编码的格式为:
1110XXXX 10XXXXXX 10XXXXXX
一般按照3部分进行编码,按照先后顺序分别是b1 b2 b3
step 1
先得到b3,b3需要得到中字符unicode编码的最后6位,需要使用与运算符,截取最后6位,使用如下字符进行与运算 00000000 00000000 00000000 00111111,运算先转换成16进制再进行运算,这个目的就是截取了unicode最后6位然后还需要将b3的前面两个已经规定好的10给添加到得到的结果的前面,使用或运算符 刚得到的与运算结果应该是00000000 00000000 00000000 00101101。使用或运算符,将10添加上,需要还进行或运算的值为 00000000 00000000 00000000 10000000,换算成16进制为0x80。
所以b3的最后结果为(0x4e2d&0x3f)|0x80
step2
然后需要得到b2,b2部分也需要截取6位,但是截取的是unicode字符刚截取部分的前面6位,这个时候如果使用逻辑右移动运算符,可以将需要截取的又放到最后6位,又可以按照刚才的方法进行截取和拼接了,先逻辑右移动6位
0x4e2d>>>6
然后再截取最后6位,使用与运算
(0x4e2d>>>6)&0x3f
最后再将10拼接到前面,使用或运算符
((0x4e2d>>>6)&0x3f)|0x80
step3
最后得到b1,可以参考前面的方法, 先逻辑右移动12位,使用逻辑右移动运算
0x4e2d>>>12
然后再截取最后4位,使用与运算
截取4位运算值为00000000 00000000 00000000 00001111
(0x4e2d>>>12)&0xf
再将1110拼接上去
拼接运算值00000000 00000000 00000000 11100000
((0x4e2d>>>12)&0xf)|0xe0
解码实例分析
如果是解码,就是把刚才编码得到的三个字节b1 b2 b3,取出编码时存入的部分,再重新按顺序拼接
b1需要取出最后4位
b1&0xf
b2需要取出最后6位
b2&0x3f
b3需要取出最后6位
b3&0x3f
最后在将取出的部分拼接起来,注意,b1需要左移动12位,b2需要左移动6位,b3不要移动
((b1&0xf)<<12)|((b2&0x3f)<<6)|b3&0x3f
最终将得到'中'字符对应的unicode编码
以下是编码解码过程代码:
@Test
public void testBinary9() {
/**
* 打印出中这个字符的unicode索引的二进制形式
*/
int i='中';
System.out.println(Integer.toBinaryString(i));//100111000101101 省略了最前面的0
//其实就是0100 1110 0010 1101,变成16进制为4e2d
}
@Test
public void testBinary10() throws UnsupportedEncodingException {
/**
* 将'中'字进行编码,变成UTF-8编码
* step1 先获得UTF-8的b3部分,使用&和|运算
*/
int a='中';
int m=0x3f;
int n=0x80;
int b3=((a&m)|n);
System.out.println(Integer.toBinaryString(a));//100111000101101
System.out.println(Integer.toBinaryString(a&m));//101101
System.out.println(Integer.toBinaryString(b3));//10101101
/**
* step2 再获取UTF-8的b2部分 使用>>>,&,|运算
*/
int k=a>>>6;
System.out.println(Integer.toBinaryString(k));//100111000
int b2=(k&m)|n;
System.out.println(Integer.toBinaryString(b2));//10111000
/**
* step3 再获取UTF-8的b1部分,使用>>>,&,|运算
*/
int s=a>>>12;
int o=0xf;
int p=0xe0;
int b1=(s&o)|p;
System.out.println(Integer.toBinaryString(b1));//11100100
//JDK提供了UTF-8到char的解码
byte[] bytes= {(byte) b1,(byte) b2,(byte)b3};
String result=new String(bytes,"utf-8");
System.out.println(result);//暂时输出乱码
/**
* 也可以手动解码,将刚才得到的三个字节按照编码方式,将放到对应位置的bit截取后重新拼接
*/
//截取b3最后6位
int c1=b3&0x3f;
//截取b2最后6位,并左移动6位
int c2=(b2&0x3f)<<6;
//截取b1最后4位,并左移动12位
int c3=(b1&0xf)<<12;
//拼接
int cResult=c3|c2|c1;
System.out.println((char)(cResult));
}
移位运算符的数学意义
十进制
移动小数点运算
123456. 小数点向右移动
1234560. 小数点向右移动1次,数字*10
12345600. 小数点向右移动2次,数字*10*10
如果小数点位置不变,数字向左移动
123456. 数字向左移动
1234560. 数字向左移动1次,数组*10
12345600. 数字向左移动2次,数组*10*10
二进制依次类推
移动小数点运算
000000000 00000000 00000000 00110010. 小数点向右移动
00000000 00000000 00000000 001100100. 小数点向右移动1次,数字*2
0000000 00000000 00000000 0011001000. 小数点向右移动2次,数字*2*2
如果小数点位置不变,数字向左移动
000000000 00000000 00000000 00110010. 数字向左移动
00000000 00000000 00000000 001100100. 数字向左移动1次,数组*2
0000000 00000000 00000000 0011001000. 数字向左移动2次,数组*2*2
数学右移位运算
1 相当如将原数据进行除法,结果向小数点方向取整数
2 >>数学移位:正数高位补0,负数高位补1,有数学意义
3 >>> 逻辑移位,不管正数负数,高位都是补0,没有数学意义
n=11111111 11111111 11111111 11110111 使用互补对称公式得出为-9
n>>1变成-5
n=111111111 11111111 11111111 1111011 使用互补对称公式得出为-5
如果n>>>1
n=011111111 11111111 11111111 1111011 非常大的一个数
部分经典面试题
(1)经典面试题:
int i=0x32;
System.out.println(i); //3*16^1+2*16^0=50
(2)经典面试题:
int n=0xffffffff;
System.out.println(n);//使用互补对称公式得出-1
(3)经典面试题:
正数的溢出为负数,负数的溢出为正数
答案:错,根据圆盘转圈,只能说不一定,要看溢出多少了,所以都有可能
(4)经典面试题:
System.out.println(~8+1);
答案:-n=~n+1公式,得到-8
(5)经典面试题:
如何优化n*8计算?
答案:n<<3; //左移位比乘法快
总结:二进制部分为计算机基础知识,有必要补充学习,加深对基础知识的理解。
参考博客;


 浙公网安备 33010602011771号
浙公网安备 33010602011771号