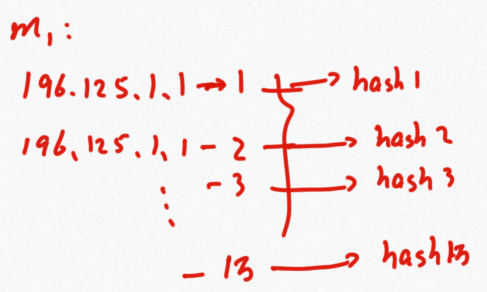Hash算法总结
目录
1 Hash函数
2 Hash冲突
3 一致性hash
hash表

1 hash函数
地址index=H(key)即根据key计算出应该存储地址的位置,而哈希表是基于哈希函数建立的一种查找表。
1.1 hash函数的性质
(1)输入域是无穷的,但是输出域是有限的
(2)不是随机产生的输出,相同的输入一定对应相同的输出
(3)不同的输入可能会导致相同的输出(hash碰撞)
(4)输出的值在整个输出域几乎是均匀分布的(离散性)
1.2 hash函数设计的考虑因素
- 计算散列地址所需要的时间(即hash函数本身不要太复杂)
- 关键字的长度
- 表长
- 关键字分布是否均匀,是否有规律可循
- 设计的hash函数在满足以上条件的情况下尽量减少冲突
2 hash冲突
不同key值产生相同的地址即:H(key1)=H(key2)
2.1 解决hash冲突的方法
- 链地址法
- 再哈希法
- 探测法
- 建立公共溢出区
2.1.1 链地址法(拉链法、链接法)
HashMap,HashSet其实都是采用的拉链法来解决哈希冲突的,就是在每个位桶实现的时候,我们采用链表(jdk1.8之后采用链表+红黑树)的数据结构来去存取发生哈希冲突的输入域的关键字(也就是被哈希函数映射到同一个位桶上的关键字)。首先来看使用拉链法解决哈希冲突的几个操作:
①插入操作:在发生哈希冲突的时候,我们输入域的关键字去映射到位桶(实际上是实现位桶的这个数据结构,链表或者红黑树)中去的时候,我们先检查带插入元素x是否出现在表中,很明显,这个查找所用的次数不会超过装载因子(n/m:n为输入域的关键字个数,m为位桶的数目),它是个常数,所以插入操作的最坏时间复杂度为O(1)的。
②查询操作:和①一样,在发生哈希冲突的时候,我们去检索的时间复杂度不会超过装载因子,也就是检索数据的时间复杂度也是O(1)的
③删除操作:如果在拉链法中我们想要使用链表这种数据结构来实现位桶,那么这个链表一定是双向链表,因为在删除一个元素x的时候,需要更改x的前驱元素的next指针的属性,把x从链表中删除。这个操作的时间复杂度也是O(1)的。
存储数据结构如下图所示:
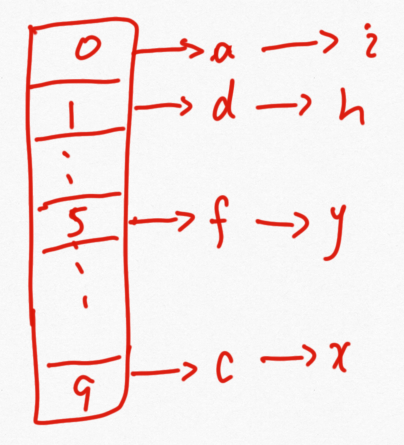
每个字符是随机均匀分布在长度为10的数组上的,因为字符多,那么在相同位置字符使用链表连接的(JDK1.8之前,从1.8之后用红黑树连接)
Java中有hashMap和hashSet这两个其实从结构上来说是一样的,可以认为value只不过是key的伴随数据而已,也就是封装的对象不同,但是基本的存储结构还是一样的。
2.1.2 再hash法
这种方式是同时构造多个哈希函数,当产生冲突时,计算另一个哈希函数的值。这种方法不易产生聚集,但增加了计算时间。
例题:
1 如果采用哈希表组织100万条记录,以支持字段A快速查找,那么以下描述中,正确的是()。
A.理论上可以在常数时间内找到特定记录 B.所有记录必须存在内存中
C.拉链式哈希法的最坏查找时间复杂度是O(n) D.哈希函数的选择与字段A无关
A:对于哈希表而言,散列冲突的问题需要解决,尤其是当数据量大的时候,散列冲突的现象将更加明显,因此,不能在常数的时间找到特定记录。B:哈希表中的数据既可以在内存中,也可以被映射到外存中(例如文件)。
C:在最坏的情况下,每个记录都有散列冲突,在这种情况下,査找的效率与线性查找的效率是一样的,时间复杂度为O(n)。D:哈希函数的选择跟字段A有直接的关系,根据A的数据类型的不同,需要选择不同的哈希函数。哈希函数的好坏对查找性能有着直接的影响。
2.1.3 探测法
一旦发生了冲突,就去寻找下一个空的散列地址,只要散列表足够大,空的散列地址总能找到,并将记录存入
公式为:fi(key) = (f(key)+di) MOD m (di=1,2,3,……,m-1)
※ 用开放定址法解决冲突的做法是:当冲突发生时,使用某种探测技术在散列表中形成一个探测序列。沿此序列逐个单元地查找,直到找到给定的关键字,或者碰到一个开放的地址(即该地址单元为空)为止(若要插入,在探查到开放的地址,则可将待插入的新结点存人该地址单元)。查找时探测到开放的地址则表明表中无待查的关键字,即查找失败。
比如说,我们的关键字集合为{12,67,56,16,25,37,22,29,15,47,48,34},表长为12。 我们用散列函数f(key) = key mod 12
当计算前S个数{12,67,56,16,25}时,都是没有冲突的散列地址,直接存入:

计算key = 37时,发现f(37) = 1,此时就与25所在的位置冲突。
于是我们应用上面的公式f(37) = (f(37)+1) mod 12 = 2。于是将37存入下标为2的位置:
可能出现的问题及解决:
当装不下时:需要进行扩容
删除数据:当需要删除数据时,有可能会造成查找不到数据比如删除了25,那么需要查37时直接就查不到了。解决方法:对删除的位置进行标记
3 一致性hash
Distributed Hash Table(DHT) 是一种哈希分布方式,其目的是为了克服传统哈希分布在服务器节点数量变化时大量数据迁移的问题。
基本原理
将哈希空间 [0, 2n-1] 看成一个哈希环,每个服务器节点都配置到哈希环上。每个数据对象通过哈希取模得到哈希值之后,存放到哈希环中顺时针方向第一个大于等于该哈希值的节点上。
最初hash用来解决服务器负载均衡问题的场景:

上图中保证了服务其存储的信息是基本均匀分布的,但是这样有一个问题,当我需要加增加一个服务器或者减少一个服务器时那么就需要重新对所有的信息取模,这样做成本太大了,因此上面的方法只适合服务器台数固定的场景使用。
为了解决上述问题提出了环形结构,按照顺时针方向把数据存储到相应的服务器中。考虑当新来一个服务器m4时,只需要把原本在m3中存储的m2~m4这段数据存储在m4中,这样只是修改了m3服务器上的部分数据,所花费的代价很少。
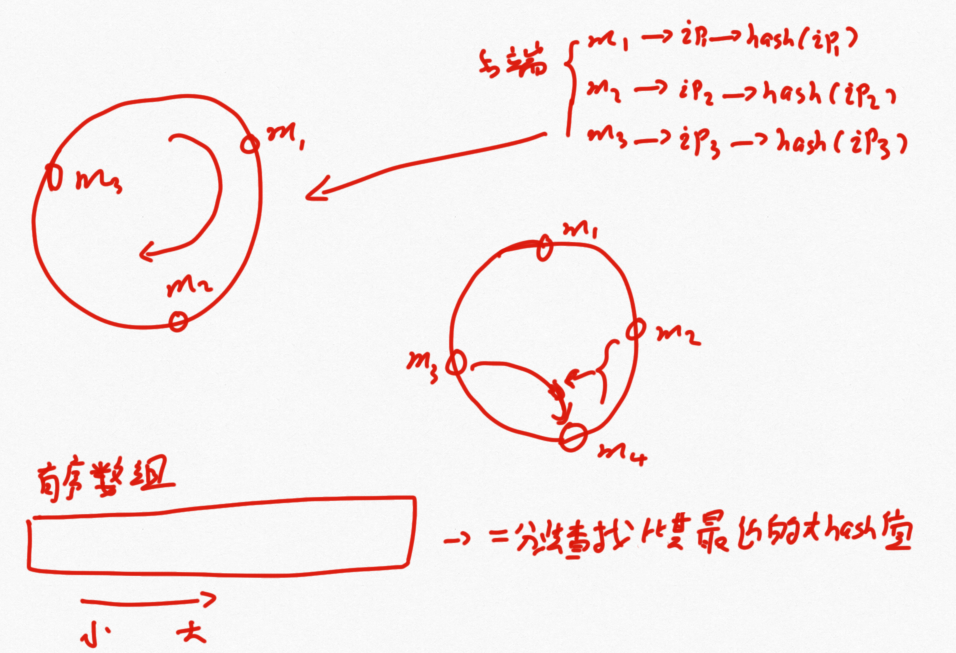
在底层实现时,是利用数组来实现环形结构,将服务器得到的hash值进行排序,得到一个有序数组,那么新来m4时,只需要二分查找比其大的最近的服务器hash值即可。
上面的方法解决了服务器数量变化的问题的,但是出现了另外两个问题:
(1)当服务器数目过少时,因为hash函数本身的性质很有可能造成某几个服务器得到hash值距离太近,这样就会导致负载不均衡问题。
(2)就算第一步问题解决了,当新增加一个服务器是,还会造成负载不均衡问题。

为了解决上面的新的分布不均的问题,提出了虚拟节点技术:三个服务器各自分配1万个虚拟节点,将虚拟节点计算出的hash值对应在环上,这样数目足够大就可以均匀分布了。
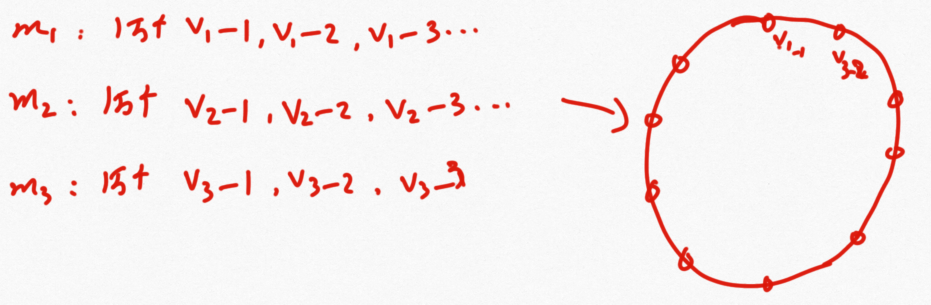
当新增一个服务器时,同样设置1万个虚拟节点,还是按照上面的顺时针迁移数据的方法,这时m1、m2、m3只需要各自移动1/12的数据即可,这样的性能还是可以接受的。
虚拟节点具体实现:
一个服务器上的对应着多个ip地址,选择其中的一万个,分别计算出hash值,将这些hash值对应在环上,即为虚拟节点