机器学习——简介

机器学习定义

• 张志华教授定义为： A field that bridge computation and statistics with ties to information, signal process, algorithm control theory and optimization theory.
• AI教父Mike Jordan的定义为：Machine Learning = Matrix + Optimization + Algorithm + Statistics
• Mitchell则给出了一个更加形象的定义：假设用P来评估计算机程序在某任务类T上的性能，若一个程序通过利用经验E在T中的任务上获得了性能改善，则我们就说关于T和P，改程序对E进行了学习。

机器学习致力于研究如何通过计算的手段，利用经验来改善系统自身的性能，从而在计算机上从数据中产生“模型”， 用于对新的情况给出判断。

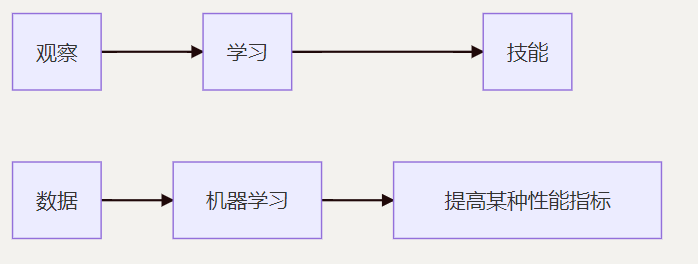
机器学习发展过程

逻辑推理阶段——人工智能发展的早期阶段

思想： 普遍认为实现人工智能的关键技术在于自动逻辑推理，只要机器被赋予逻辑推理能力就可以实现人工智能
成果： 主要通过谓词逻辑演算模拟人类智能。这个阶段的人工智能的主流核心技术是符号逻辑计算，在数学定理自动证明等领域获得了一定成功

专家系统——以知识工程为核心技术

提出原因： 如果没有一定数量专业领域知识支撑，则很难实现对复杂实际问题的逻辑推理
成果： 专家系统使用基于专家知识库的知识推理取代纯粹的符号逻辑计算，在故障诊断、游戏博弈等领域取得了巨大成功
方法： 专家系统需要针对具体问题的专业领域特点建立相应的专家知识库，利用这些知识来完成推理和决策
缺陷： 将专家知识总结出来并以适当的方式告诉计算机程序有时非常困难，通常需要针对每个具体任务手工建立相应的知识库
总结： 专家知识的人工获取和表示方式严重制约了人工智能的进一步发展

机器学习

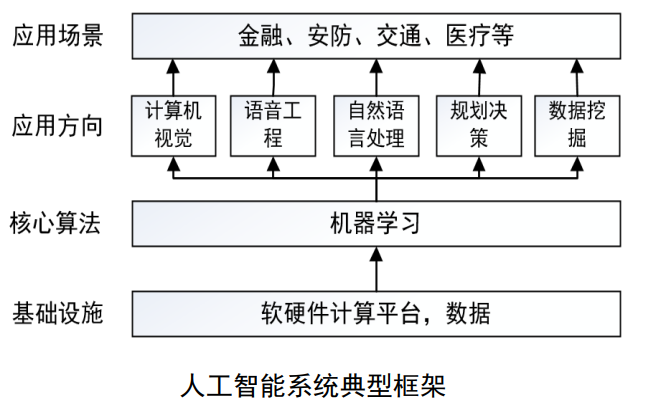
发展： 20世纪90年代中期以来，机器学习得到迅速发展并逐步取代传统专家系统成为人工智能的主流核心技术，使得人工智能逐步进入机器学习时代。目前，以机器学习为主流核心技术的人工智能在多个领域取得的巨大成功已使其成为社会各界关注的焦点和引领社会未来的战略性技术 （如下图所示）

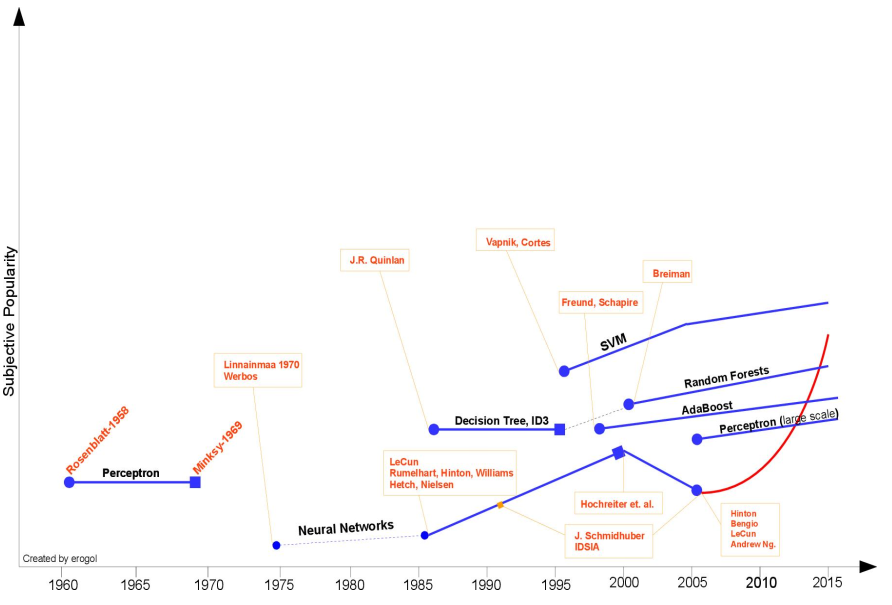
机器学习早期各时期盛行的技术、方法

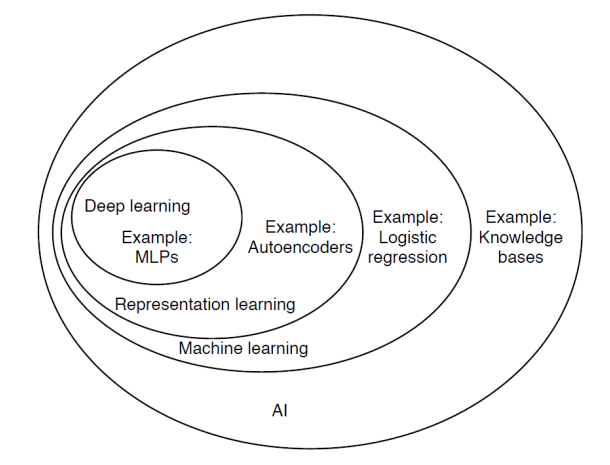
机器学习和其他领域之间的关系：

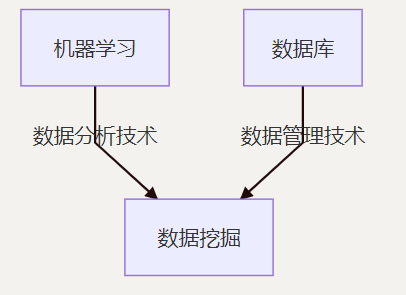
机器学习的分类

• 有监督学习：利用一组带标注样本调整模型参数，提升模型性能的学习方式。 基本思想是通过标注值告诉模型在给定输入的情况下应该输出什么值，由此获得尽可能接近真实映射方式的优化模型
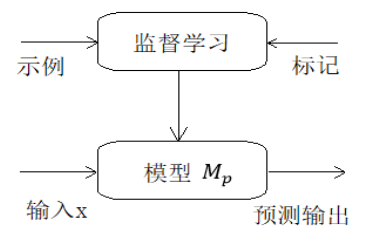
  有标记、有反馈、预测结果

• 弱监督学习：利用标注数据和未标注数据学习预测，预测模型的机器学习问题。通常是有少量标注标签、大量未标注数据，因为标注数据的构建往往需要人工，成本较高，未标注数据的收集不需要太多成本。

  1. 不充分学习：半监督学习、PU学习
  2. 不准确学习：多示例学习、偏标记学习
  3. 不精确学习：标签噪声学习

• 无监督学习：通过比较样本之间的某种联系实现对样本的数据分析。 最大特点是学习算法的输入是无标记样本
  无标记、无反馈、挖掘内在结构

• 强化学习：根据反馈信息来调整机器行为以实现自动决策的一种机器学习方式。 强化学习主要由智能体和环境两个部分组成。智能体是行为的实施者，由基于环境信息的评价函数对智能体的行为做出评价，若智能体的行为正确，则由相应的回报函数给予智能体正向反馈信息以示奖励，反之则给予智能体负向反馈信息以示惩罚
  
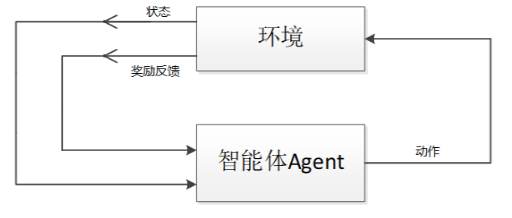
  决策过程、奖励机制、学习一系列动作

• 主动学习：指机器不断主动给出实例让人进行标注，然后利用标注数据学习预测模型的机器学习问题。通常的监督学习使用给定的标注数据，往往是随机得到的，可以看作是“被动学习”，主动学习的目标是找出对学习最有帮助的实例让人标注，以较小的标注代价，达到较好的效果。

机器学习的任务

一般来说，机器学习面向的任务有三类：回归问题、分类问题、聚类问题

他们往往都是需要构建一个模型来确定，利用各种机器学习方法提升模型的泛化能力（即模型面对未知数据的处理能力）

机器学习的归纳偏好

机器学习的归纳偏好有很多，这里介绍两个常用的：

• No Free Lunch Theorem：一个算法\(\xi_a\)如果在某些问题上比另一个算法\(\xi_b\) 好，必然存在另一些问题,\(\xi_b\)比\(\xi_a\)好
• Ocam's razor: 若多个假设与观察一致，则选择最简单的那个

归纳偏好对应学习算法本身所作出的关于“什么样的模型更好”的假设。在具体的现实问题中，这个假设是否成立，即算法的归纳偏好是否与问题本身匹配，大多时候直接决定了算法能都取得好的性能。

损失函数和验证方法

损失函数可以参考两篇博客：损失函数、交叉验证方法

结构风险最小化与经验风险最小化

经验风险最小化（Empirical Risk Minimization）的策略认为，经验风险最小的模型是最优的模型。根据这一策略，安装经验风险最小化求最优模型就是求解最优化问题

\[\min_{f\in \mathcal{F}}\frac{1}{N}\sum_{i=1}^NL(y_i,f(x_i)),\qquad \mathcal{F}是假设空间 \]

当样本容量足够大，经验风险最小化能保证有很好的学习效果。（有足够的数据，包括所有发生的可能，全部给模型学习，模型的性能就会很准确），在现实中国被广泛采用。例如极大似然估计（Maximum Likehood Estimate）

但是当样本数量不够大的时候，经验风险最小化的效果就不是很好了，易产生过拟合。结构风险最小化（Structural Risk Minimization）是为了防止过拟合而提出的策略。结构风险最小化等价于正则化。结构风险在经验风险上加上了表示模型复杂度的正则化项（亦称惩罚项）。

\[\min_{f\in \mathcal{F}}\frac{1}{N}\sum_{i=1}^NL(y_i,f(x_i))+\lambda\mathcal{J}(f),\qquad \mathcal{F}是假设空间,\ \mathcal{J}是模型复杂度 \]

结构风险最小化的应用即是最大后验概率（Maximum Posterior Probability Estimate）

参考：
李航 统计机器学习
周志华 机器学习（西瓜书）
张志华 机器学习导论